双対性議論(duality argument)について

関数解析
2016.12.30
関数解析

$p\in[1,\infty)$のとき

  • Lebesgue空間$L^{p}(\R^N)$の共役空間$L^{p}(\R^N)^{*}$
  • Lebesgue空間$L^{p’}(\R^N)$

が同型であることはよく知られています(すなわち，$p’$は$p$のHölder共役)．

この同型$(L^{p})^{*}\cong L^{p’}$について，次の$L^p$双対性が成り立ちます：任意の$v\in L^{p’}(\Omega)$に対して

    \begin{align*}\|v\|_{L^{p'}(\Omega)} =\sup_{\|u\|_{L^{p}(\Omega)}=1}\abs{\int_{\Omega}u(x)v(x)\,dx}.\end{align*}

また，同様に$L^pL^q$空間でも双対性の等式が成り立ちます．

これらの双対性を用いる論法を双対性議論 (duality argument)などといいます．

この記事では，これら$L^p$双対性，$L^pL^q$双対性に関する等式を証明します．

準備

ここでは本題に入る前に

  • 定義関数
  • Hölder共役

の定義を確認しておきます．

定義関数

定義関数を以下で定義します．

[定義関数]　集合$A$とその部分集合$B$に対して

    \begin{align*}f(x):=\left\{\begin{aligned}&1&&(x\in B)\\&0&&(x\notin B)\end{aligned}\right.\end{align*}

で定まる写像$f:A\to\R$を$B$上の定義関数であるという．

この記事では$\Omega\subset\R^N$に対して，$\Omega$上の定義関数$\R^N\to\R$を$I_{\Omega}$と表します：

    \begin{align*}I_{\Omega}(x):=\left\{\begin{aligned}&1&&(x\in\Omega),\\&0&&(x\notin\Omega).\end{aligned}\right.\end{align*}

Hölder共役

Hölder共役を定義します．

[Hölder共役]　$p\in[1,\infty]$に対して

    \begin{align*}\frac{1}{p'}+\frac{1}{p}=1 \bra{\iff p'=\bra{1-\frac{1}{p}}^{-1}}\end{align*}

で定まる$p’\in[1,\infty]$を$p$のHölder共役という．ただし，$p=1$のときは$p’=\infty$とみなし，$p=\infty$のときは$p’=1$とみなす．

例えば，

  • $p=2$のHölder共役$p’$は$p’=2$
  • $p=3$のHölder共役$p’$は$p’=3/2$
  • $p=5/2$のHölder共役$p’$は$p’=5/3$

ですね．

$L^p$空間の双対性議論

まず$L^p$空間の双対性を説明します．

$L^p$空間

まずは$L^{p}$空間の定義を確認します．

[$L^p$空間]　$\Omega\subset\R^N$を開集合とし，$p\in[1,\infty]$とする．このとき，ノルム

    \begin{align*}\|u\|_{p}=\|u\|_{L^{p}(\Omega)}:=\left\{\begin{aligned} &\bra{\int_{\Omega}|u(x)|^{p}\,dx}^{1/p}&&(p\in[1,\infty))\\ &\operatorname{ess\, sup}\limits_{x\in\Omega}|u(x)|&&(p=\infty) \end{aligned}\right.\end{align*}

を備えたLebesgue(ルベーグ)可測な関数全部の空間を$L^p(\Omega)$と表す．

$L^p(\Omega)$は「ノルム$\|\cdot\|_p$を備えた$p$乗Lebesgue可積分な関数全部の空間」ということもできますね．

$L^p$空間の双対性

冒頭で述べたように，$L^p$空間の双対性について以下が成り立つ．

[$L^{p}$空間の双対性]　$\Omega\subset\R^N$を開集合とし，$p\in[1,\infty)$とする．このとき，任意の$v\in L^{p’}(\Omega)$に対して，

    \begin{align*}\|v\|_{p'}=\sup_{\|u\|_{p}=1}\abs{\int_{\Omega}u(x)v(x)\,dx}\end{align*}

が成り立つ．ただし，$p’\in(1,\infty]$は$p$のHölder共役である．


Hölderの不等式より，任意の$v\in L^{p’}(\Omega)$に対して，

    \begin{align*}\sup_{\|u\|_{p}=1}\abs{\int_{\Omega}u(x)v(x)\,dx} \le\sup_{\|u\|_{p}=1}\|u\|_{p}\|v\|_{p'} =\|v\|_{p'}\end{align*}

だから，あとは

    \begin{align*}\sup_{\|u\|_{p}=1}\abs{\int_{\Omega}u(x)v(x)\,dx} \ge\|v\|_{p'}\end{align*}

を示せば[$L^{p}$空間の双対性]が従う．これを

  • $p=1$のとき
  • $p\in(1,\infty)$のとき

に分けて示す．

[１]　$p=1$のとき，$p’=\infty$である．

任意の$\epsilon>0$に対して，ある可測集合$\Omega’\subset\Omega$で$0<|\Omega’|<\infty$を満たすものが存在して

    \begin{align*}x\in\Omega'\Ra|v(x)|>\|v\|_{\infty}-\epsilon\end{align*}

が成り立つ．このとき，$w:\Omega\to\C$を

    \begin{align*}w(x):=\frac{\overline{v(x)}}{|\Omega'||v(x)|}I_{\Omega'}(x)\end{align*}

で定めると

    \begin{align*}\|w\|_{p} =\int_{\Omega}|w(x)|\,dx =\frac{1}{|\Omega'|}\int_{\Omega'}\,dx=1\end{align*}

だから

    \begin{align*}&\sup_{\|u\|_{p}=1}\abs{\int_{\Omega}u(x)v(x)\,dx} \\\ge&\abs{\int_{\Omega}w(x)v(x)\,dx} =\abs{\frac{1}{|\Omega'|}\int_{\Omega'}\frac{\overline{v(x)}v(x)}{|v(x)|}\,dx} \\=&\frac{1}{|\Omega'|}\int_{\Omega'}|v(x)|\,dx >\frac{1}{|\Omega'|}\int_{\Omega'}(\|v\|_{\infty}-\epsilon)\,dx \\=&\|v\|_{\infty}-\epsilon\end{align*}

となって，$\epsilon$の任意性から$\sup\limits_{\|u\|_{p}=1}\abs{\dint_{\Omega}u(x)v(x)\,dx}\ge\|v\|_{\infty}$が従う．

[２]　$p\in(1,\infty)$のとき，$p’\in(1,\infty)$である．

$\theta_{x}:=\arg v(x)$とし，$w:\Omega\to\C$を$w(x):=\dfrac{|v(x)|^{p’-1}}{\|v\|_{p’}^{p’/p}}e^{-i\theta_{x}}$で定める．このとき，

    \begin{align*}\|w\|_{p} =&\bra{\int_{\Omega}|w(x)|^{p}\,dx}^{1/p} \\=&\frac{1}{\|v\|_{p'}^{p'/p}}\bra{\int_{\Omega}|v(x)|^{p(p'-1)}\,dx}^{1/p} \\=&\frac{1}{\|v\|_{p'}^{p'/p}}\bra{\int_{\Omega}|v(x)|^{p'}\,dx}^{1/p} =1\end{align*}

だから

    \begin{align*}&\sup_{\|u\|_{p}=1}\abs{\int_{\Omega}u(x)v(x)\,dx} \\\ge&\abs{\int_{\Omega}w(x)v(x)\,dx} =\abs{\frac{1}{\|v\|_{p'}^{p'/p}}\int_{\Omega}|v(x)|^{p'-1}e^{-i\theta_{x}}|v(x)|e^{i\theta_{x}}\,dx} \\=&\frac{1}{\|v\|_{p'}^{p'/p}}\int_{\Omega}|v(x)|^{p'}\,dx =\|v\|_{p'}^{p'-\frac{p'}{p}} =\|v\|_{p'}\end{align*}

が従う．

$L^pL^q$空間の双対性

次に，$L^pL^q$空間の双対性を説明します．

$L^pL^q$空間

まずは$L^{p}L^{q}$空間を定義します．

[$L^pL^q$空間]　$i=1,2$に対して，$\Omega_i\subset\R^{N_i}$を開集合とし，$p,q\in[1,\infty]$とする．このとき，ノルム

    \begin{align*}\|u\|_{L^{p}L^{q}}=\|u\|_{p,q}:=\brb{\int_{\Omega_1}\bra{\int_{\Omega_2}|u(x_1,x_2)|^{q}\,dx_2}^{p/q}\,dx_1}^{1/q}\end{align*}

が有限なLebesgue可測な関数全部の空間を$L^{p}L^{q}(\Omega_1\times\Omega_2)$や$L^p(\Omega_1;L^q(\Omega_2))$などと表す．

この$L^{p}L^{q}$空間は，例えば時間発展する非線形偏微分方程式で

  • 空間$\R^n$に関して$L^{p}$
  • 時間$\R$に関して$L^{q}$

である場合などに用います．

シュレディンガー方程式の分散性｜基本解のLpLq評価の導出
シュレディンガー方程式の基本解に関してLpLq評価という基本的な不等式があります．LpLq評価はシュレディンガー方程式を考える上で重要なストリッカーツ評価のベースとなります．
math-note.xyz

$L^pL^q$空間の双対性

$L^p$空間の双対性と同様に，$L^{p}L^{q}$空間について以下が成り立つ．

[$L^{p}L^{q}$空間の双対性]　$i=1,2$に対して，$\Omega_i\subset\R^{N_i}$を開集合とし，$p_i\in[1,\infty)$とする．このとき，任意の$v\in L^{p’_1}(\Omega_1;L^{p’_2}(\Omega_2))$に対して，

    \begin{align*}\|v\|_{p'_1,p'_2} =\sup_{\|u\|_{p_1,p_2}=1}\abs{\int_{\Omega_1}\int_{\Omega_2}u(x_1,x_2)v(x_1,x_2)\,dx_2dx_1}\end{align*}

が成り立つ．ただし，$p’_i\in(1,\infty]$は$p_i$のHölder共役である($i=1,2$)．


$x:=(x_1,x_2)$とする．Hölderの不等式より，任意の$v\in L^{p’_1}(\Omega_1;L^{p’_2}(\Omega_2))$に対して，

    \begin{align*}&\sup_{\|u\|_{p_1,p_2}=1}\abs{\int_{\Omega_1}\bra{\int_{\Omega_2}u(x)v(x)\,dx_2}\,dx_1} \\\le&\sup_{\|u\|_{p_1,p_2}=1}\int_{\Omega_1}\abs{\int_{\Omega_2}u(x)v(x)\,dx_2}dx_1 \\\le&\sup_{\|u\|_{p_1,p_2}=1}\int_{\Omega_1}\|u(x_1,\cdot)\|_{p_1}\|v(x_1,\cdot)\|_{p'_1}\,dx_1 \\\le&\sup_{\|u\|_{p_1,p_2}=1}\|u\|_{p_1,p_2}\|v\|_{p'_1,p'_2} =\|v\|_{p'_1,p'_2}\end{align*}

だから，あとは

    \begin{align*}\sup_{\|u\|_{p_1,p_2}=1}\abs{\int_{\Omega_1}\bra{\int_{\Omega_2}u(x)v(x)\,dx_2}\,dx_1} \ge\|v\|_{p'_1,p'_2}\end{align*}

を示せば[$L^{p}L^{q}$空間の双対性]が従う．これを

  • $p_1=p_2=1$のとき
  • $p_1=1$, $p_2\in(1,\infty)$のとき
  • $p_1,p_2\in(1,\infty)$のとき

に分けて証明する．

[１]　$p_1=p_2=1$のとき，$p’_1=p’_2=\infty$である．

任意の$\epsilon>0$, $i\in\{1,2\}$に対して，ある可測集合$\Omega’_i\subset\Omega$で$0<|\Omega’_i|<\infty$を満たすものが存在して，$x\in\Omega’_1\times\Omega_2$が成り立つなら

    \begin{align*}|v(x)|>\|v(x_1,\cdot)\|_{L^{\infty}(\Omega_2)}-\epsilon >\|v\|_{p'_1,p'_2}-2\epsilon\end{align*}

が成り立つ．このとき，$w:\Omega_1\times\Omega_2\to\C$を

    \begin{align*}w(x):=\frac{\overline{v(x)}}{|\Omega'_1||\Omega'_2|v(x)}I_{\Omega'_1\times\Omega'_2}(x)\end{align*}

で定めると

    \begin{align*}\|w\|_{p_1,p_2} =&\int_{\Omega_1}\bra{\int_{\Omega_2}|w(x)|\,dx_2}\,dx_1 \\=&\frac{1}{|\Omega'_1||\Omega'_2|}\int_{\Omega'_1}\bra{\int_{\Omega'_2}\,dx_2}\,dx_1 =1\end{align*}

だから

    \begin{align*}&\sup_{\|u\|_{p_1,p_2}=1}\abs{\int_{\Omega_1}\bra{\int_{\Omega_2}u(x)v(x)\,dx_2}\,dx_1} \\\ge&\abs{\int_{\Omega_1}\bra{\int_{\Omega_2}w(x)v(x)\,dx_2}\,dx_1} \\=&\abs{\frac{1}{|\Omega'_1||\Omega'_2|}\int_{\Omega'_1}\bra{\int_{\Omega'_2}\frac{\overline{v(x)}v(x)}{v(x)}\,dx_2}\,dx_1} \\=&\frac{1}{|\Omega'_1||\Omega'_2|}\int_{\Omega'_1}\bra{\int_{\Omega'_2}|v(x)|\,dx_2}\,dx_1 \\>&\frac{1}{|\Omega'_1||\Omega'_2|}\int_{\Omega'_1}\bra{\int_{\Omega'_2}(\|v\|_{p'_1,p'_2}-2\epsilon)\,dx_2}\,dx_1 \\=&\|v\|_{p'_1,p'_2}-2\epsilon\end{align*}

となって，$\epsilon$の任意性から$\sup\limits_{\|u\|_{p_1,p_2}=1}\abs{\dint_{\Omega_1}\bra{\int_{\Omega_2}u(x)v(x)\,dx_2}\,dx_1}\ge\|v\|_{p’_1,p’_2}$が従う．

[２]　$p_1=1,p_2\in(1,\infty)$のとき，$p’_1=\infty,p’_2\in(1,\infty)$である．

任意の$\epsilon>0$に対して，ある可測集合$\Omega’_1\subset\Omega_1$で$0<|\Omega’_1|<\infty$を満たすものが存在して，$x\in\Omega’_1\times\Omega_2$が成り立つとき，

    \begin{align*}\|v(x_1,\cdot)\|_{L^{p'_2}(\Omega_2)} >\|v\|_{1,p'_2}-\epsilon\end{align*}

が成り立つ．このとき，$\theta_{x}:=\arg v(x)$とし，$w:\Omega_1\times\Omega_2\to\C$を

    \begin{align*}w(x):=\frac{|v(x)|^{p'_2-1}}{|\Omega'_1|\|v(x_1,\cdot)\|_{L^{p'_2}(\Omega_2)}^{p'_2/p_2}}e^{-i\theta_{x}}I_{\Omega'_1\times\Omega_2}(x)\end{align*}

で定めると

    \begin{align*}\|w\|_{p_1,p_2} =&\int_{\Omega_1}\bra{\int_{\Omega_2}|w(x)|^{p_2}\,dx_2}^{1/p_2}\,dx_1 \\=&\frac{1}{|\Omega'_1|}\int_{\Omega'_1}\frac{1}{\|v(x_1,\cdot)\|_{L^{p'_2}(\Omega_2)}^{p'_2/p_2}}\bra{\int_{\Omega_2}|v(x)|^{p_2(p'_2-1)}\,dx_2}^{1/p_2}\,dx_1 \\=&\frac{1}{|\Omega'_1|}\int_{\Omega'_1}\frac{1}{\|v(x_1,\cdot)\|_{L^{p'_2}(\Omega_2)}^{p'_2/p_2}}\bra{\int_{\Omega_2}|v(x)|^{p'_2}\,dx_2}^{1/p_2}\,dx_1 \\=&\frac{1}{|\Omega'_1|}\int_{\Omega'_1}\,dx_1=1\end{align*}

だから

    \begin{align*}&\sup_{\|u\|_{p_1,p_2}=1}\abs{\int_{\Omega_1}\bra{\int_{\Omega_2}u(x)v(x)\,dx_2}\,dx_1} \\\ge&\abs{\int_{\Omega_1}\bra{\int_{\Omega_2}w(x)v(x)\,dx_2}\,dx_1} \\=&\abs{\frac{1}{|\Omega'_1|}\int_{\Omega'_1}\bra{\frac{1}{\|v(x_1,\cdot)\|_{L^{p'_2}(\Omega_2)}^{p'_2/p_2}}\int_{\Omega_2}|v(x)|^{p'_2-1}e^{-i\theta_{x}}v(x)\,dx_2}\,dx_1} \\=&\frac{1}{|\Omega'_1|}\int_{\Omega'_1}\bra{\frac{1}{\|v(x_1,\cdot)\|_{L^{p'_2}(\Omega_2)}^{p'_2/p_2}}\int_{\Omega_2}|v(x)|^{p'_2}\,dx_2}\,dx_1 \\=&\frac{1}{|\Omega'_1|}\int_{\Omega'_1}\|v(x_1,\cdot)\|_{L^{p'_2}(\Omega_2)}^{p'_2-\frac{p'_2}{p_2}}\,dx_1 =\frac{1}{|\Omega'_1|}\int_{\Omega'_1}\|v(x_1,\cdot)\|_{L^{p'_2}(\Omega_2)}\,dx_1 \\>&\frac{1}{|\Omega'_1|}\int_{\Omega'_1}(\|v\|_{p'_1,p'_2}-\epsilon)\,dx_1 =\|v\|_{p'_1,p'_2}-\epsilon\end{align*}

となって，$\epsilon$の任意性から$\sup\limits_{\|u\|_{p_1,p_2}=1}\abs{\dint_{\Omega_1}\bra{\int_{\Omega_2}u(x)v(x)\,dx_2}\,dx_1}\ge\|v\|_{p’_1,p’_2}$が従う．

[３]　$p_1,p_2\in(1,\infty)$のとき，$p’_1,p’_2\in(1,\infty)$である．

$\theta_{x}:=\arg v(x)$とし，$w:\Omega_1\times\Omega_2\to\C$を

    \begin{align*}w(x) :=\frac{|v(x)|^{p'_2-1}}{\|v\|_{p'_1,p'_2}^{p'_1/p_1} \|v(x_1,\cdot)\|_{L^{p'_2} (\Omega_2)}^{1-p'_1+p'_2/p_2}}e^{-i\theta_{x}}\end{align*}

で定めると

    \begin{align*}&\bra{\int_{\Omega_1}\abs{\int_{\Omega_2}|w(x)|^{p_2}\,dx_2}^{p_1/p_2}\,dx_1}^{1/p_2} \\=&\frac{1}{\|v\|_{p'_1,p'_2}^{p'_1/p_1}}\bra{\int_{\Omega'_1}\frac{1}{\|v(x_1,\cdot)\|_{L^{p'_2}(\Omega_2)}^{p_1(1-p'_1+p'_2/p_2)}}\bra{\int_{\Omega_2}|v(x)|^{p_2(p'_2-1)}\,dx_2}^{p_1/p_2}\,dx_1}^{1/p_1} \\=&\frac{1}{\|v\|_{p'_1,p'_2}^{p'_1/p_1}}\bra{\int_{\Omega'_1}\frac{1}{\|v(x_1,\cdot)\|_{L^{p'_2}(\Omega_2)}^{p_1(1-p'_1+p'_2/p_2)}}\bra{\int_{\Omega_2}|v(x)|^{p'_2}\,dx_2}^{p_1/p_2}\,dx_1}^{1/p_1} \\=&\frac{1}{\|v\|_{p'_1,p'_2}^{p'_1/p_1}}\bra{\int_{\Omega'_1}\|v(x_1,\cdot)\|_{L^{p'_2}(\Omega_2)}^{p_1(p'_1-1)}\,dx_1}^{1/p_1} \\=&\frac{1}{\|v\|_{p'_1,p'_2}^{p'_1/p_1}}\bra{\int_{\Omega'_1}\|v(x_1,\cdot)\|_{L^{p'_2}(\Omega_2)}^{p'_1}\,dx_1}^{1/p_1} =1\end{align*}

である．すなわち$\|w\|_{p_1,p_2}=1$だから

    \begin{align*}&\sup_{\|u\|_{p_1,p_2}=1}\abs{\int_{\Omega_1}\bra{\int_{\Omega_2}u(x)v(x)\,dx_2}\,dx_1} \\\ge&\abs{\int_{\Omega_1}\bra{\int_{\Omega_2}w(x)v(x)\,dx_2}\,dx_1} \\=&\abs{\frac{1}{\|v\|_{p'_1,p'_2}^{p'_1/p_1}}\int_{\Omega_1}\bra{\frac{1}{\|v(x_1,\cdot)\|_{L^{p'_2}(\Omega_2)}^{1-p'_1+p'_2/p_2}}\int_{\Omega_2}|v(x)|^{p'_2-1}e^{-i\theta_{x}}v(x)\,dx_2}\,dx_1} \\=&\frac{1}{\|v\|_{p'_1,p'_2}^{p'_1/p_1}}\int_{\Omega_1}\bra{\frac{1}{\|v(x_1,\cdot)\|_{L^{p'_2}(\Omega_2)}^{1-p'_1+p'_2/p_2}}\int_{\Omega_2}|v(x)|^{p'_2}\,dx_2}\,dx_1 \\=&\frac{1}{\|v\|_{p'_1,p'_2}^{p'_1/p_1}}\int_{\Omega_1}\bra{\frac{1}{\|v(x_1,\cdot)\|_{L^{p'_2}(\Omega_2)}^{1-p'_1+p'_2/p_2}}\|v(x_1,\cdot)\|_{L^{p'_2}(\Omega_2)}^{p'_2}}\,dx_1 \\=&\frac{1}{\|v\|_{p'_1,p'_2}^{p'_1/p_1}}\int_{\Omega_1}\|v(x_1,\cdot)\|_{L^{p'_2}(\Omega_2)}^{p'_1-1+p'_2(1-1/p_2)}\,dx_1 \\=&\frac{1}{\|v\|_{p'_1,p'_2}^{p'_1/p_1}}\int_{\Omega_1}\|v(x_1,\cdot)\|_{L^{p'_2}(\Omega_2)}^{p'_1}\,dx_1 \\=&\frac{1}{\|v\|_{p'_1,p'_2}^{p'_1/p_1}}\|v\|_{p'_1,p'_2}^{p'_1} =\|v\|_{p'_1,p'_2}^{p'_1(1-1/p_1)} =\|v\|_{p'_1,p'_2}\end{align*}

が従う．

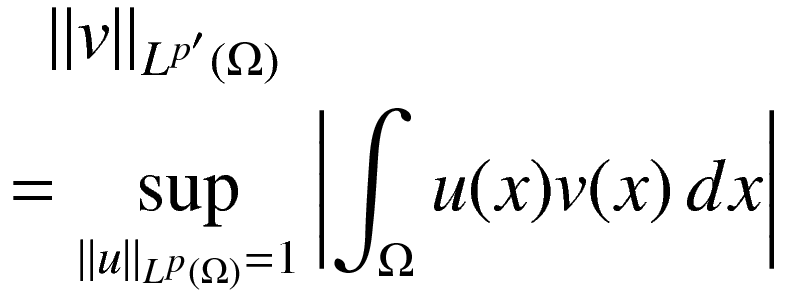
コメント