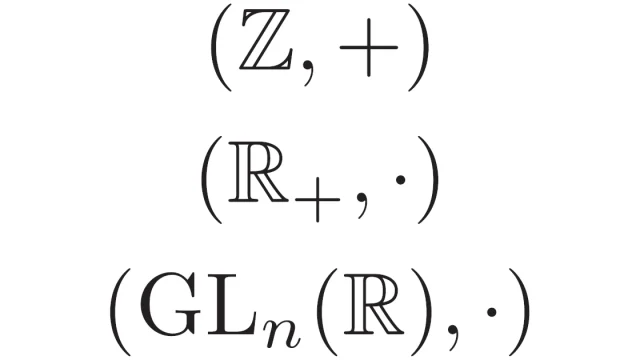 群論の基本
群論の基本 群の定義・考え方を具体例から解説|群論は集合と演算の分野
群を扱う群論は代数学の基礎となる分野のひとつ分野です.群は3つの性質[結合法則][単位元の存在][逆元の存在]を満たす集合と演算のことをいいます.この記事では群の定義と具体例を解説します.
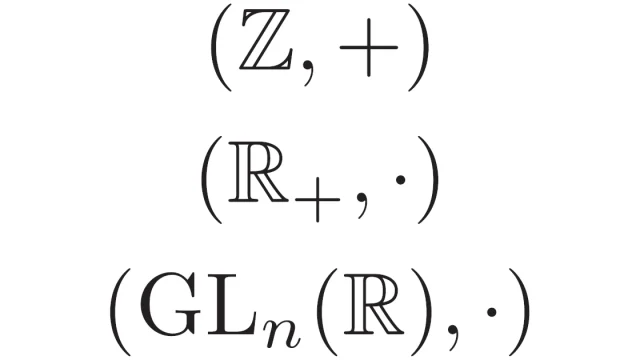 群論の基本
群論の基本 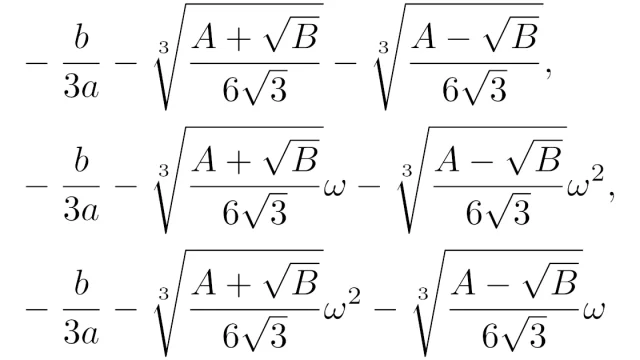 代数学
代数学 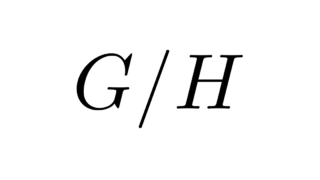 代数学
代数学 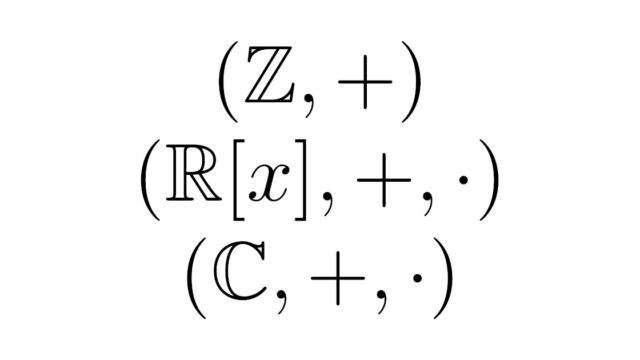 代数学
代数学