単関数近似定理｜ルベーグ可測関数fを単関数列{fₙ}で近似する

ルベーグ積分はルベーグ可測関数に対して定義される積分で，ルベーグ可測関数はルベーグ可測単関数により近似できるという定理があります．

このことは可測関数の単関数近似と呼ばれており，ルベーグ可測関数の定義の背景にある重要な性質です．

この記事では

ルベーグ可測関数の単関数近似定理と考え方
単関数近似定理の証明

を順に説明します．

以下ではルベーグ可測集合のことを単に「可測集合」と呼びます．また，ルベーグ可測関数のことを単に「可測関数」と呼びます．

「ルベーグ積分の基本」の一連の記事

ルベーグ積分入門
1. 0 ルベーグ積分の基礎｜リーマン積分の先へ！積分の歴史から紹介

ルベーグ測度

ルベーグ可測関数とルベーグ積分

ルベーグ積分の性質と項別積分

ルベーグ積分の参考文献
1. ルベグ積分入門
2. ルベーグ積分と関数解析
ルベーグ可測関数の単関数近似定理と考え方
単関数近似定理の証明
非負値とは限らない場合の単関数近似定理

ルベーグ積分の参考文献

以下はルベーグ積分に関するオススメの教科書です．

ルベグ積分入門

ロングセラーの入門書です．専門書ですが，文庫なので安く購入できるのも魅力です．

ルベーグ積分と関数解析

ルベーグ積分から更なるステップに進みたい人向けの教科書です．

ルベーグ可測関数の単関数近似定理と考え方

冒頭で説明したように，可測関数は次のように単関数で近似することができます．

［単関数近似定理］可測集合$A$上の非負値可測関数$f$に対して，ある非負値単関数列$\{f_n\}$が存在して，

任意の$n$に対して$f_n$は可測関数
任意の$x\in A$に対して$0\le f_1(x)\le f_2(x)\le\dots$
任意の$x\in A$に対して$\lim\limits_{n\to\infty}f_n(x)=f(x)$

が成り立つ．

言葉で言えば，「非負可測関数は非負可測単関数列により下から近似できる」ということになりますね．

この定理は具体的に可測単関数列$\{f_n\}$を構成することにより証明できるので，具体的に$f_1$と$f_2$をどのように構成すれば良いかを解説します．

$f_1$の構成

まず$f_1$を

$0\le f(x)<\dfrac{1}{2}$なる$x\in A$で値$0$
$\dfrac{1}{2}\le f(x)<1$なる$x\in A$で値$\dfrac{1}{2}$
$1\le f(x)$なる$x\in A$で値$1$

をとる単関数と定めましょう．

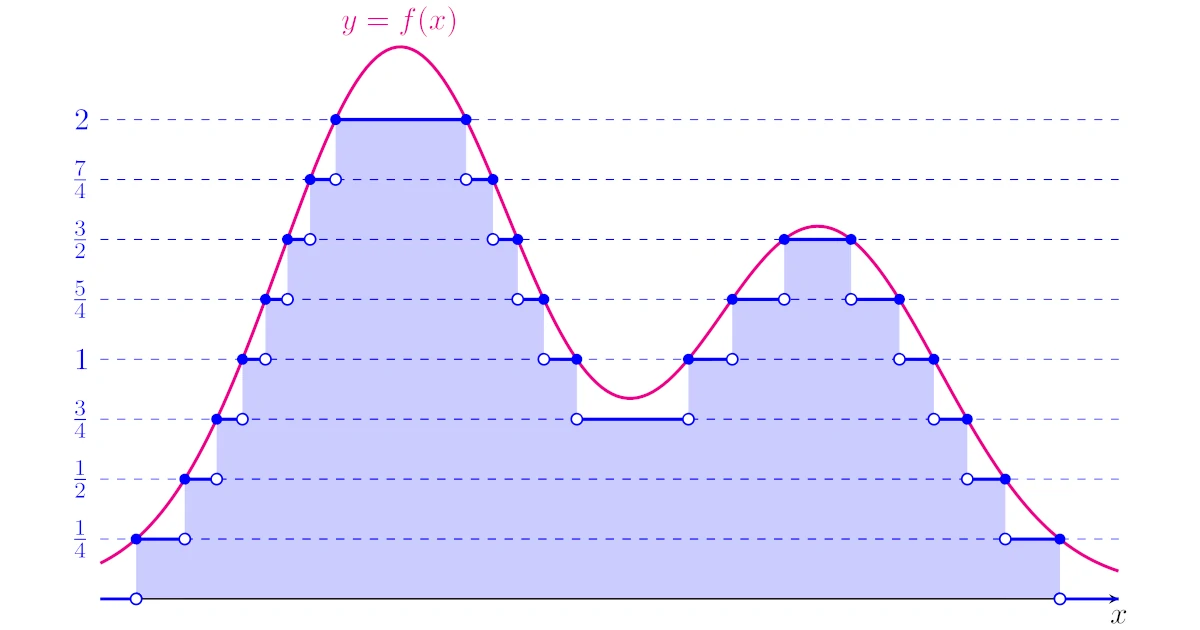
つまり，$0$から$1$までを幅$\dfrac{1}{2}$で「横切り」して単関数をつくるわけですね．

$f_2$の構成

次に$f_2$を

$0\le f(x)<\dfrac{1}{4}$なる$x\in A$で値$0$
$\dfrac{1}{4}\le f(x)<\dfrac{1}{2}$なる$x\in A$で値$\dfrac{1}{4}$
$\dfrac{1}{2}\le f(x)<\dfrac{3}{4}$なる$x\in A$で値$\dfrac{1}{2}$
……
$\dfrac{7}{4}\le f(x)<2$なる$x\in A$で値$\dfrac{7}{4}$
$2\le f(x)$なる$x\in A$で値$2$

をとる単関数と定めましょう．

つまり，$0$から$2$までを幅$\dfrac{1}{4}$で「横切り」して単関数をつくるわけですね．

$f_n$の構成

いまの$f_1$, $f_2$の調子で$f_n$を

$0\le f(x)<\dfrac{1}{2^n}$なる$x\in A$で値$0$
$\dfrac{1}{2^n}\le f(x)<\dfrac{2}{2^n}$なる$x\in A$で値$\dfrac{1}{2^n}$
$\dfrac{2}{2^n}\le f(x)<\dfrac{3}{2^n}$なる$x\in A$で値$\dfrac{2}{2^n}$
……
$n-\dfrac{1}{2^n}\le f(x)<n$なる$x\in A$で値$n-\dfrac{1}{2^n}$
$n\le f(x)$なる$x\in A$で値$n$

と定めます．つまり，$0$から$n$までを幅$\dfrac{1}{2^n}$で「横切り」してできる単関数を$f_n$とするわけですね．

このように，刻み幅をどんどん小さくし，最大の値をどんどん大きくして行くと，条件を満たす単関数列$\{f_n\}$ができあがりそうですね．

単関数近似定理の証明

単関数近似定理の証明のために，単関数が可測関数であるための必要十分条件を思い出しておきましょう．

可測集合$A$上の単関数$f$が有限個の値$\alpha_1,\dots,\alpha_n$のみとるとき，次は同値である．

$f$は$A$上の可測関数
任意の$k\in\{1,2,\dots,n\}$に対して$\set{x\in A}{f(x)=\alpha_k}$は可測集合

この補題が効いて，上で考えた構成で各$f_n$が単関数になっていることが分かります．

［単関数近似定理（再掲）］可測集合$A$上の非負値可測関数$f$に対して，ある非負値単関数列$\{f_n\}$が存在して，

任意の$n$に対して$f_n$は可測関数
任意の$x\in A$に対して$0\le f_1(x)\le f_2(x)\le\dots$
任意の$x\in A$に対して$\lim\limits_{n\to\infty}f_n(x)=f(x)$

が成り立つ．

$n\in\N$に対して，$f_n:A\to\R_{\ge0}$を

$\begin{align*}f(x)=\begin{cases}\frac{k}{2^n}&(\frac{k}{2^n}\le f(x)<\frac{k+1}{2^n};k=0,1,\dots,n2^n)\\n&(n\le f(x))\end{cases}\end{align*}$

と定める．このとき，$f_n$がとる値は$0,\frac{1}{2^{n}},\frac{2}{2^{n}},\dots,n-\frac{1}{2^{n}},n$の有限個だから，$\{f_n\}$は単関数列である．

［可測性］任意の$k\in\{0,1,2,\dots,n\cdot2^n-1\}$に対して，$f$は可測関数だから

$\begin{align*}\set{x\in A}{\frac{k}{2^{n}}\le f(x)<\frac{k+1}{2^{n}}}\end{align*}$

は可測集合となり，上で示した補題より$f_n$は可測関数である．

［単調性］任意に$n\in\N$, $k\in\{0,1,\dots,n2^n-1\}$をとる．

$\frac{k}{2^n}\le f(x)<\frac{k+1}{2^n}$なる$x\in A$に対して，$f_n(x)=\frac{k}{2^n}$であることに注意しておく．

$\frac{k}{2^n}\le f(x)<\frac{k+\frac{1}{2}}{2^n}$なる$x\in A$に対して，$\frac{2k}{2^{n+1}}\le f(x)<\frac{2k+1}{2^{n+1}}$だから
$\begin{align*}f_n(x)=\frac{k}{2^n}=\frac{2k}{2^{n+1}}=f_{n+1}(x)\end{align*}$
$\frac{k+\frac{1}{2}}{2^n}\le f(x)<\frac{k+1}{2^n}$なる$x\in A$に対して，$\frac{2k+1}{2^{n+1}}\le f(x)<\frac{2k+2}{2^{n+1}}$だから
$\begin{align*}f_n(x)=\frac{k}{2^n}\le\frac{2k+1}{2^{n+1}}=f_{n+1}(x)\end{align*}$