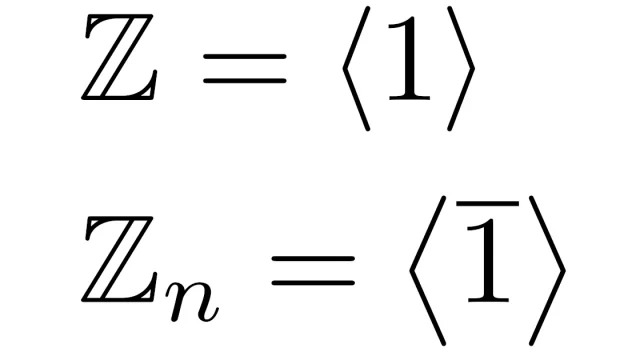 群論の基本
群論の基本 生成される部分群の考え方を具体例から解説|巡回群も紹介
群(G,・)に対し,いくつかのg₁,g₂,……,gₙ∈Gとそれらの逆元を演算してできるGの元全部の集合は群(G,・)の部分群になり,この群を{g₁,g₂,……,gₙ}により生成される部分群といい,〈g₁,g₂,……,gₙ〉と表します.
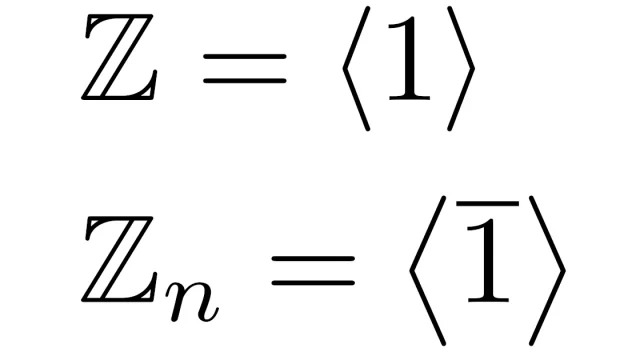 群論の基本
群論の基本 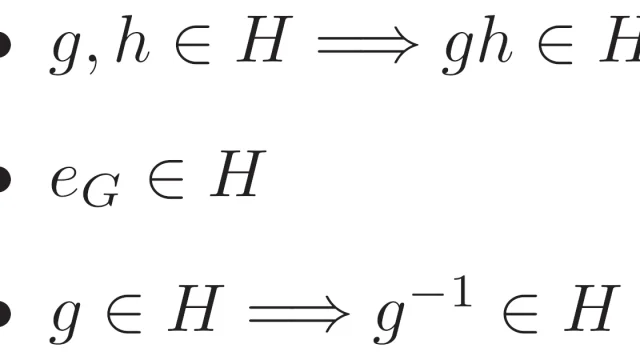 群論の基本
群論の基本 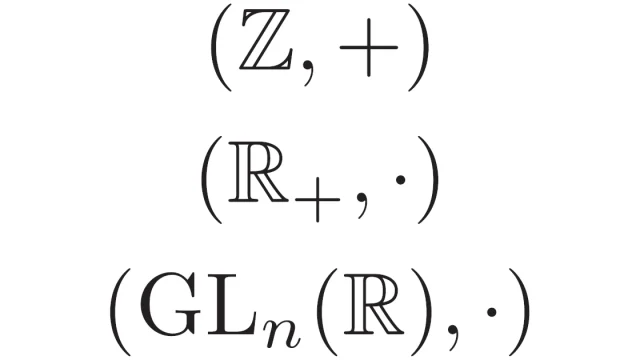 群論の基本
群論の基本