 集合論
集合論 関数の表し方|“f”と“f(x)”で意味はどう違う?
高校数学では「関数f(x)」という表現が,大学数学では「関数f」という表現が多く用いられています.実はこれら“f"と“f(x)"の意味には明確な違いがあり,この記事ではこの違いを説明しています.
 集合論
集合論 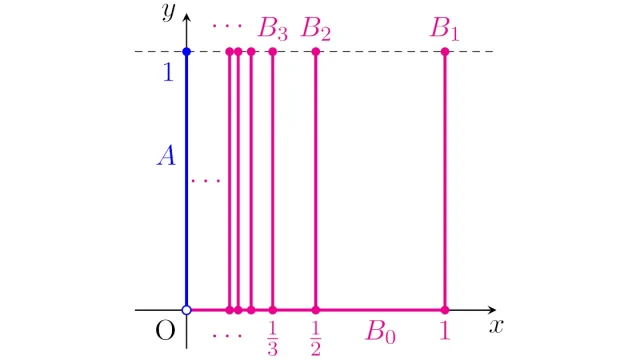 位相空間論
位相空間論 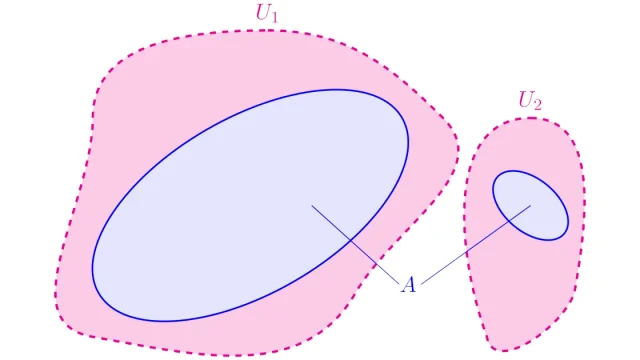 位相空間論
位相空間論 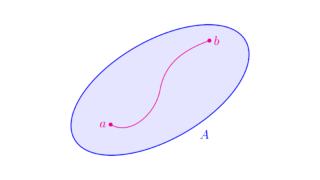 位相空間論
位相空間論 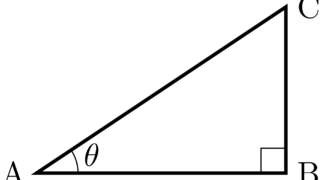 集合論
集合論  位相空間論
位相空間論  集合論
集合論  位相空間論
位相空間論 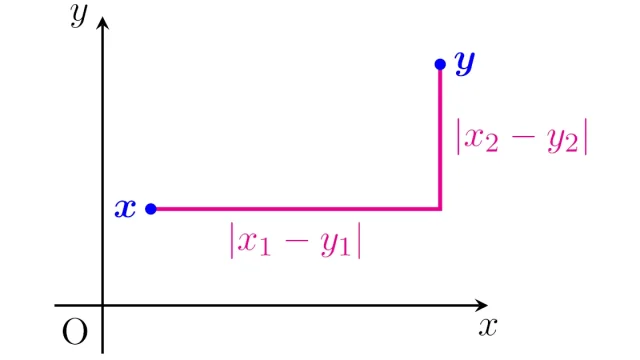 位相空間論
位相空間論 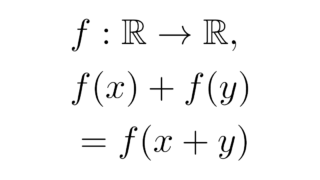 集合論
集合論