 複素解析
複素解析 フレネル積分を複素積分で計算する|cos(x²),sin(x²)の広義積分
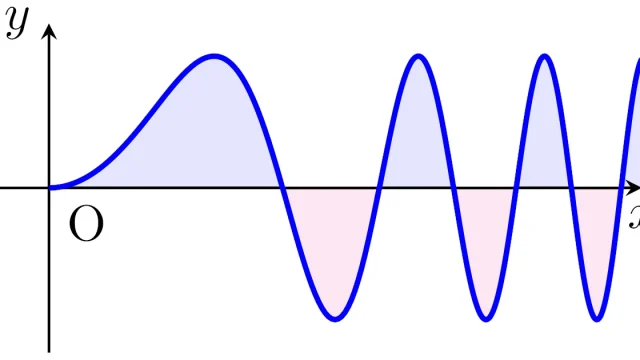
0≦xでのcos(x²), sin(x²)の広義リーマン積分を「フレネル積分」といいます.フレネル積分は複素積分に持ち込み,コーシーの積分定理を用いることにより計算することができます.また,一般化したcos(xⁿ), sin(xⁿ)の広義リーマン積分も計算しています.
 複素解析
複素解析  複素解析
複素解析  複素解析の基本
複素解析の基本  複素解析の基本
複素解析の基本 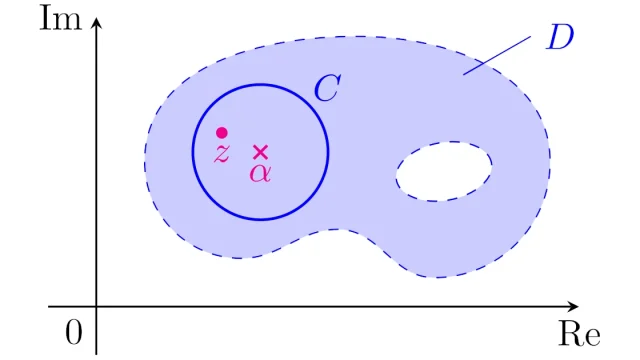 複素解析の基本
複素解析の基本 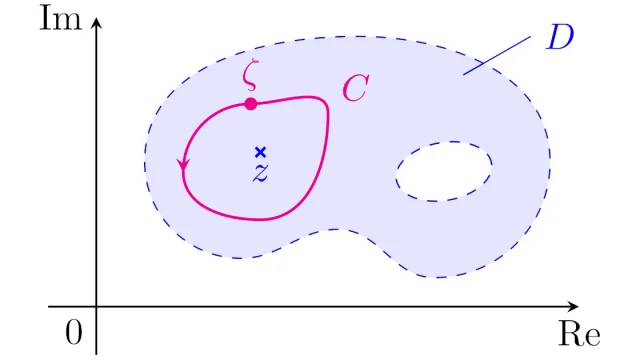 複素解析の基本
複素解析の基本 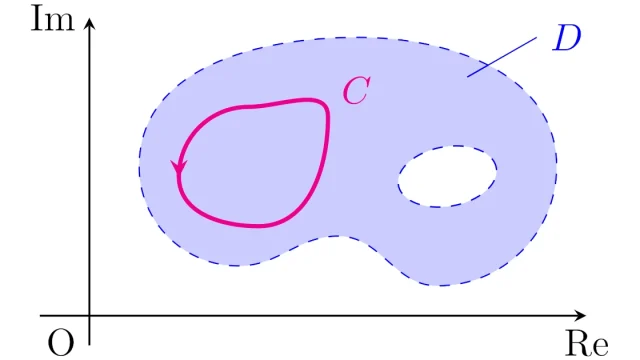 複素解析の基本
複素解析の基本 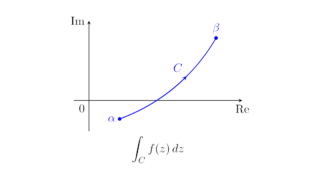 複素解析の基本
複素解析の基本  複素解析の基本
複素解析の基本  複素解析の基本
複素解析の基本