「ルベーグ積分の基本」の一連の記事
- ルベーグ積分入門
- ルベーグ測度
- ルベーグ可測関数とルベーグ積分
「ルベーグ積分の基本」の一連の記事
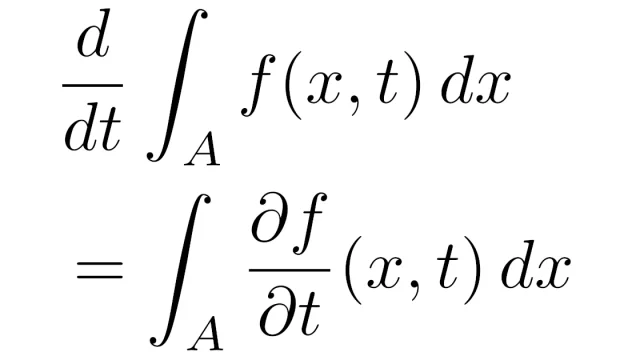 ルベーグ積分の基本
ルベーグ積分の基本 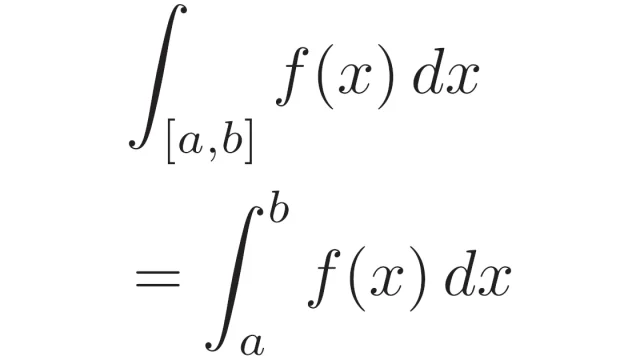 ルベーグ積分の基本
ルベーグ積分の基本 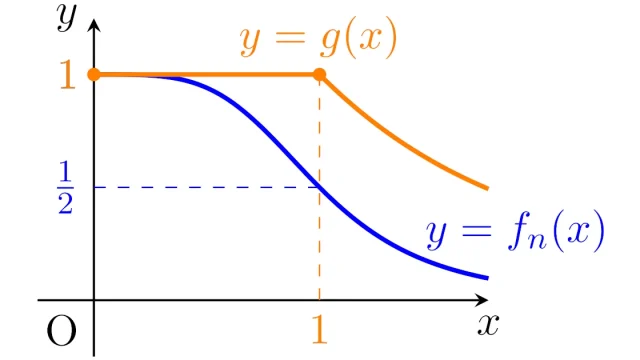 ルベーグ積分の基本
ルベーグ積分の基本 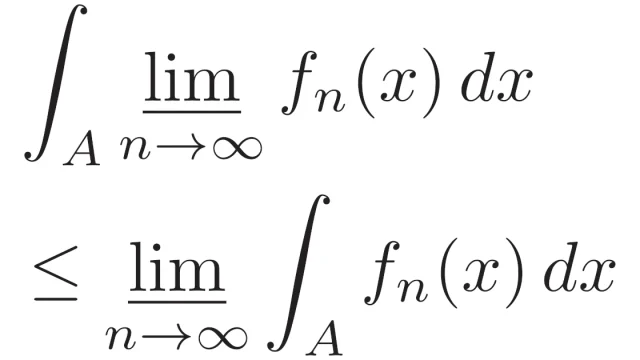 ルベーグ積分の基本
ルベーグ積分の基本 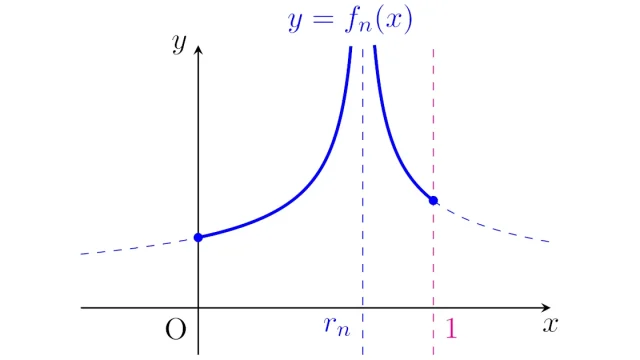 ルベーグ積分の基本
ルベーグ積分の基本 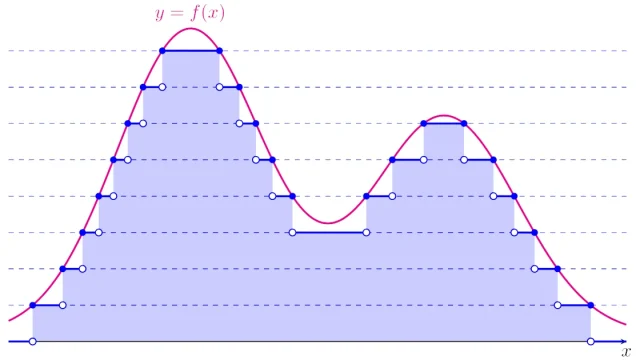 ルベーグ積分の基本
ルベーグ積分の基本 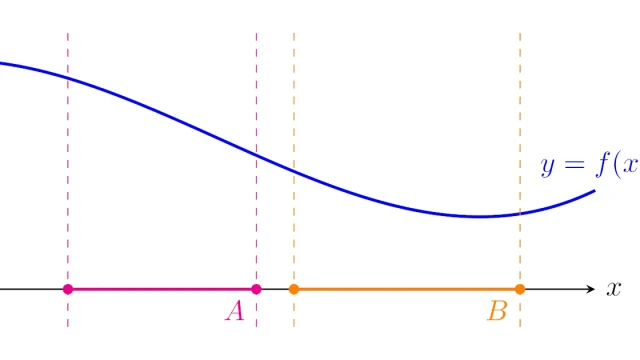 ルベーグ積分の基本
ルベーグ積分の基本 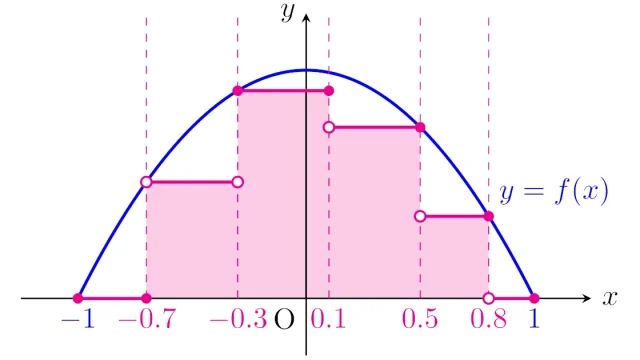 ルベーグ積分の基本
ルベーグ積分の基本 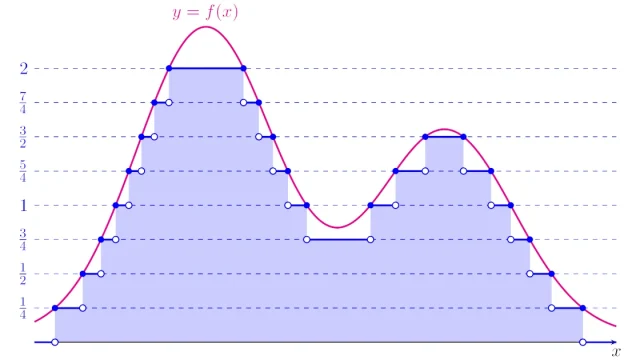 ルベーグ積分の基本
ルベーグ積分の基本 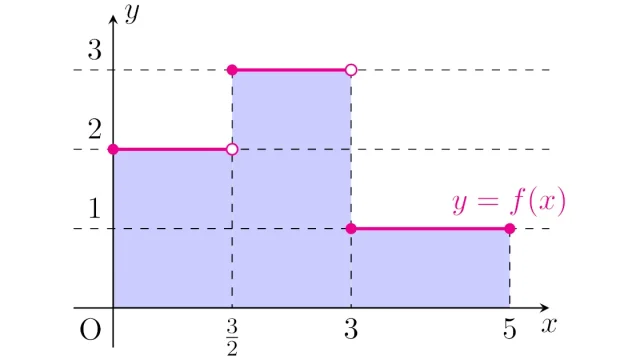 ルベーグ積分の基本
ルベーグ積分の基本