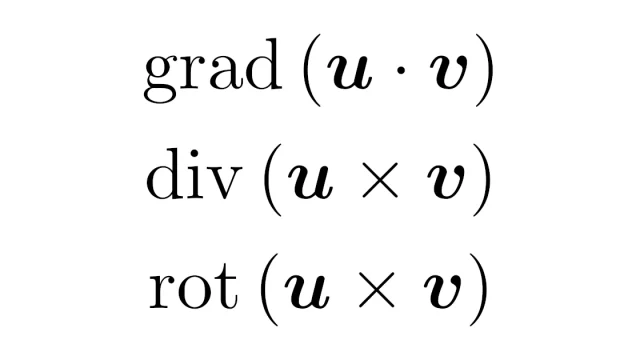ベクトル解析gradとdivとrot｜ベクトル解析の基本の微分公式のまとめ
ベクトル解析では３つの基本の微分作用素gradとdivとrotを計算できることは大切です．計算の中では[和の微分公式]，[積の微分公式]，[内積・外積の微分公式]を用いる機会が多くあります．この記事では，これらの微分公式をまとめます．
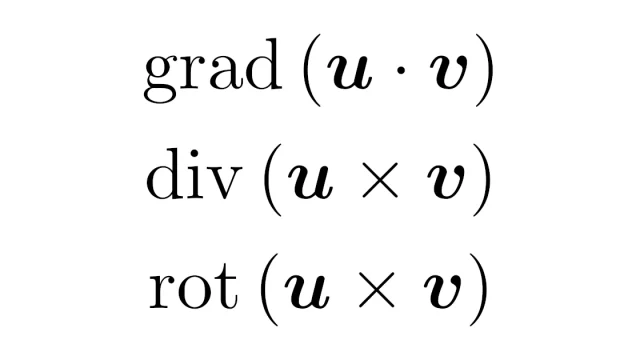ベクトル解析
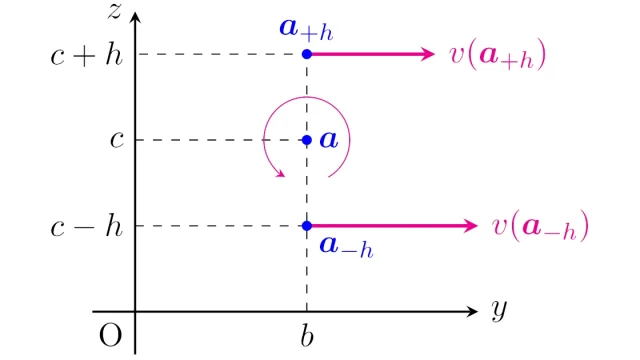ベクトル解析
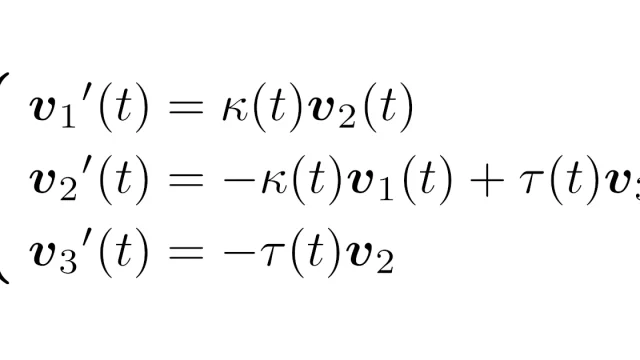ベクトル解析gradとdivとrotの定義と直感的な考え方｜ナブラ∇に関する微分作用素
ベクトル解析においては，勾配grad，発散div，回転rot(curl)の３つが重要な微分作用素で，数学のみならず物理でも広く現れます．この記事では，この３つの微分作用素の定義とイメージを説明し，これらのナブラ∇による表し方も説明します．
ベクトル解析フルネ-セレの公式の導出｜曲線の曲率と捩率の公式
[Frenet-Serretの公式]は３次元の曲線上に関する「接ベクトル」「主法線ベクトル」「従法線ベクトル」の関係式です．大学１年で学ぶ線形代数と微分積分の知識で導くことができる曲線曲面論の公式です．