 複素解析の基本
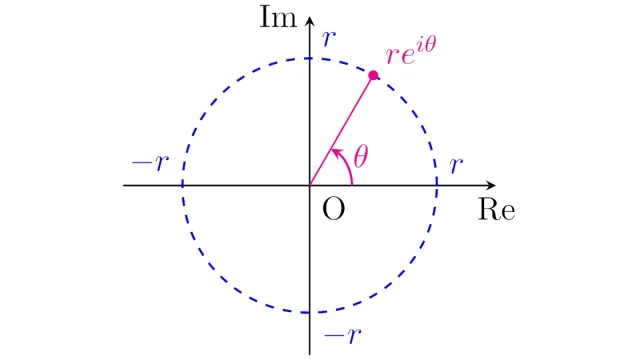
複素解析の基本 複素関数sin,cos,expの定義と諸性質|オイラーの公式と指数法則
複素関数の三角関数cos(z),sin(z)と指数関数eᶻは整級数(冪級数)を用いて定義するのが一般的です.また,この定義からオイラーの公式eᶻ=cos(z)+isin(z),指数法則eᶻ⁺ᵛ=eᶻeᵛを導くことができます.
 複素解析の基本
複素解析の基本  微分方程式
微分方程式 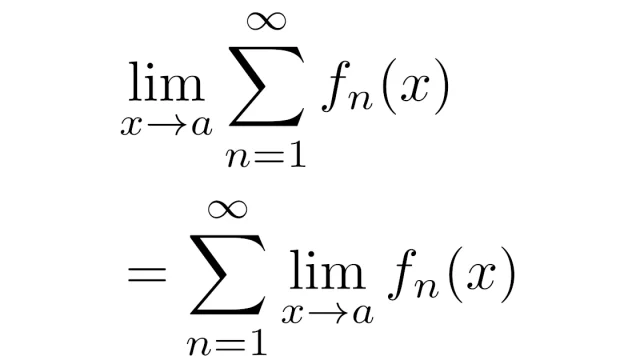 測度論
測度論 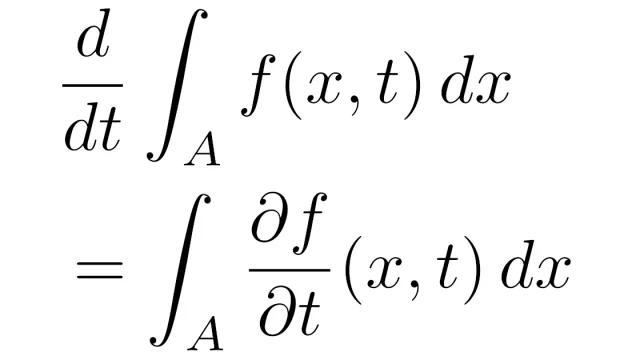 ルベーグ積分の基本
ルベーグ積分の基本  複素解析
複素解析 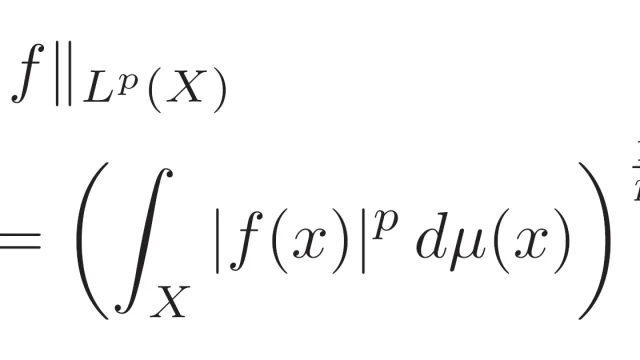 ルベーグ空間
ルベーグ空間 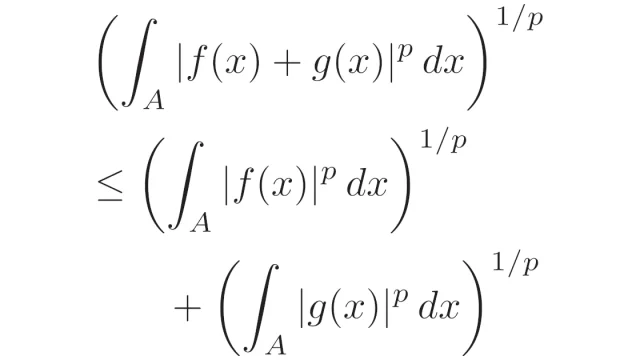 ルベーグ空間
ルベーグ空間 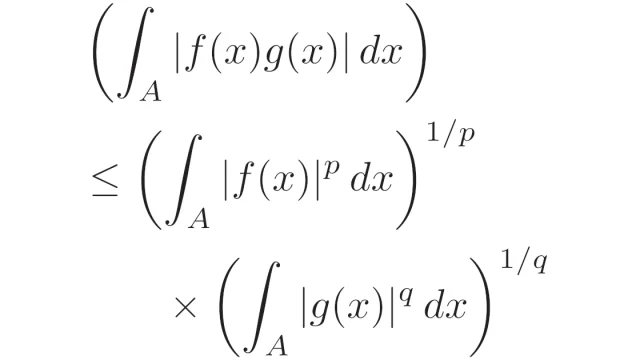 ルベーグ空間
ルベーグ空間 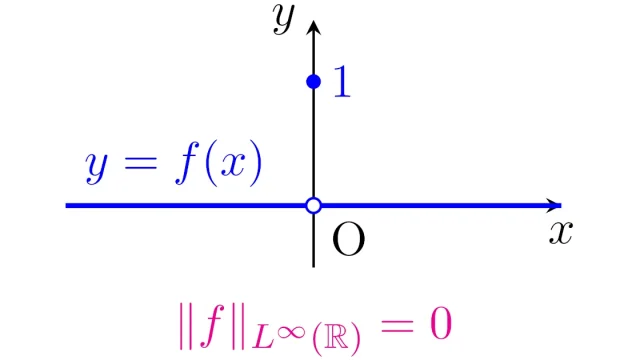 ルベーグ空間
ルベーグ空間 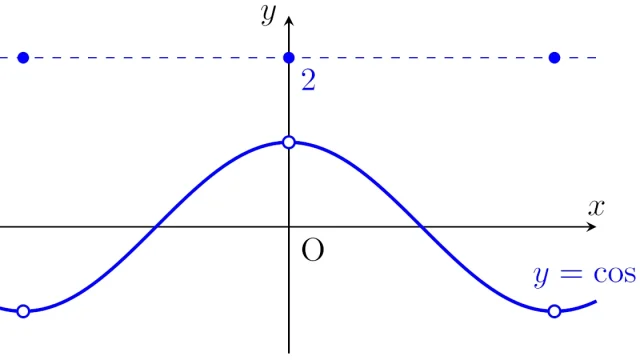 ルベーグ空間
ルベーグ空間