 線形空間の基本
線形空間の基本 線形空間の基底の定義・基本性質|証明のテンプレートも紹介
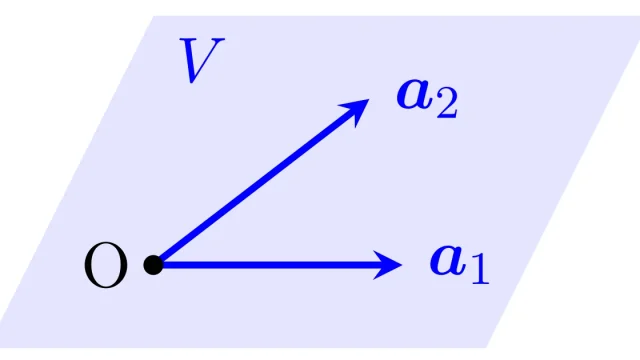
一般に,線型空間Vのベクトルv₁,v₂,……,vₙが(1)Vを生成し(2)全て線形独立であるとき,組(v₁,v₂,……,vₙ)をVの基底といいます.この記事では,基底であることの定義・具体例を説明し,基底による線形結合の一意性も証明します.
 線形空間の基本
線形空間の基本 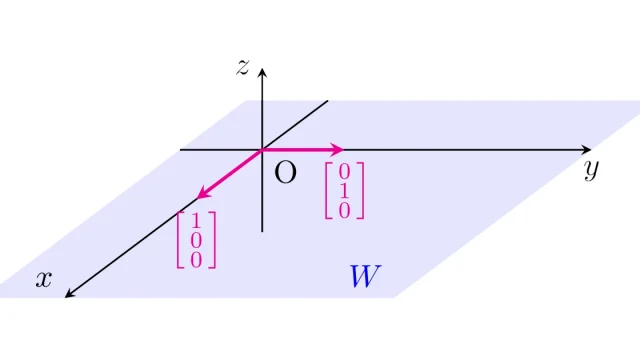 線形空間の基本
線形空間の基本 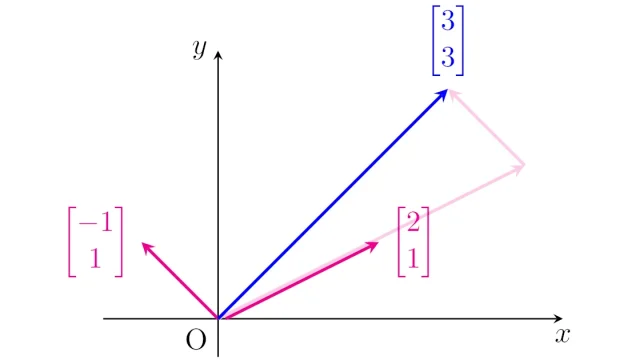 線形空間の基本
線形空間の基本 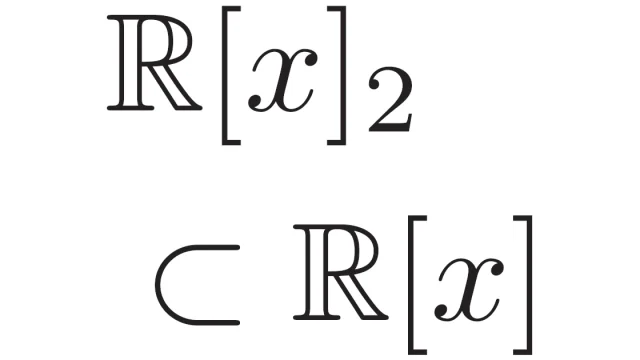 線形空間の基本
線形空間の基本  線形空間の基本
線形空間の基本