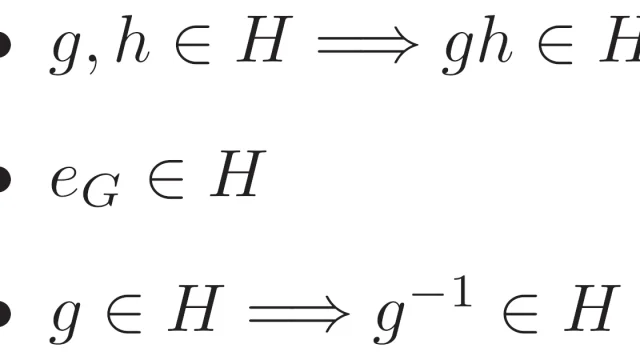 群論の基本
群論の基本 部分群の定義・具体例|部分群であることの証明テンプレも紹介
部分群とは,もとの群の集合の空でない部分集合で,もとの群と同じ演算で閉じていて,群となっているもののことを言います.この記事では部分群の定義・具体例・性質を解説し,部分群であることの証明のテンプレートも説明します.
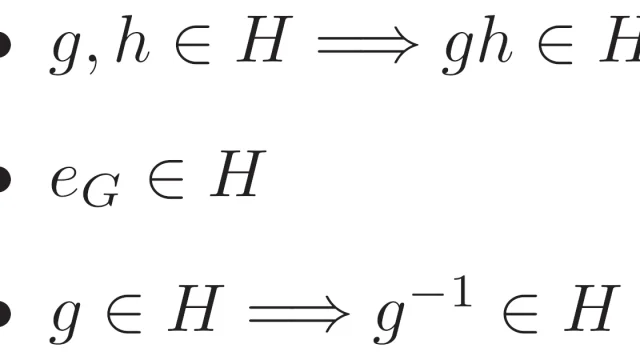 群論の基本
群論の基本 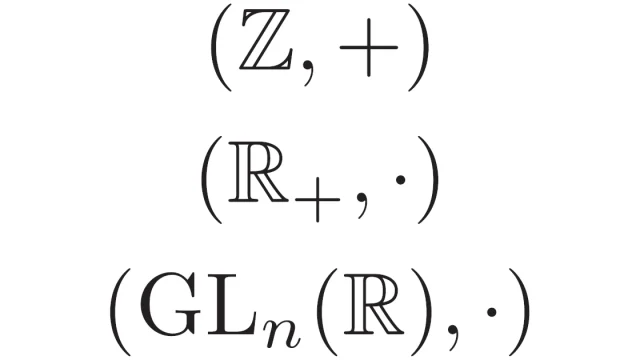 群論の基本
群論の基本 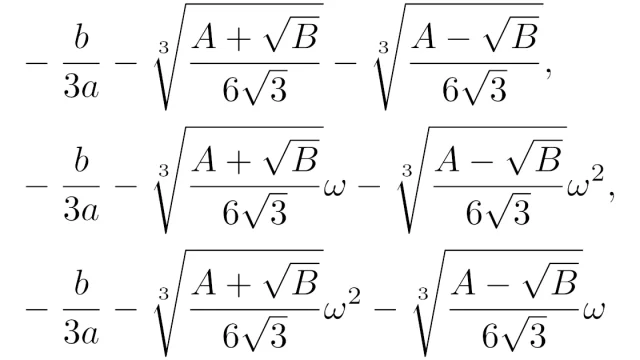 代数学
代数学 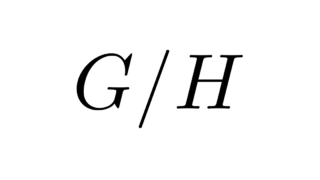 代数学
代数学 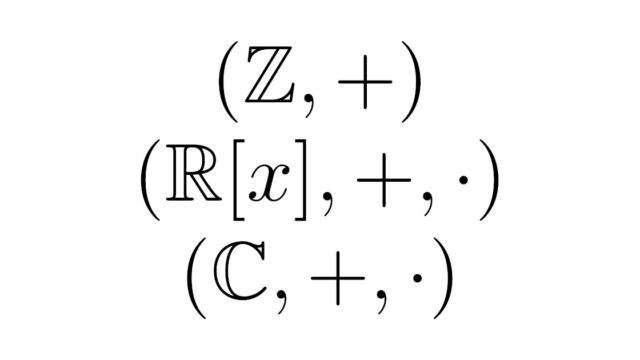 代数学
代数学