 重要な確率分布
重要な確率分布 ポアソン分布Po(λ)とは?定義と期待値・分散・母関数の計算
「事象が時間あたりに起こる回数」が従う確率分布をポアソン分布といいます.この記事では,ポアソン分布を定義して,具体例を紹介します.そのあと,定義から期待値E[X],分散V[X],母関数を求めます.
 重要な確率分布
重要な確率分布  確率分布の性質
確率分布の性質  重要な確率分布
重要な確率分布  重要な確率分布
重要な確率分布  重要な確率分布
重要な確率分布  重要な確率分布
重要な確率分布  重要な確率分布
重要な確率分布 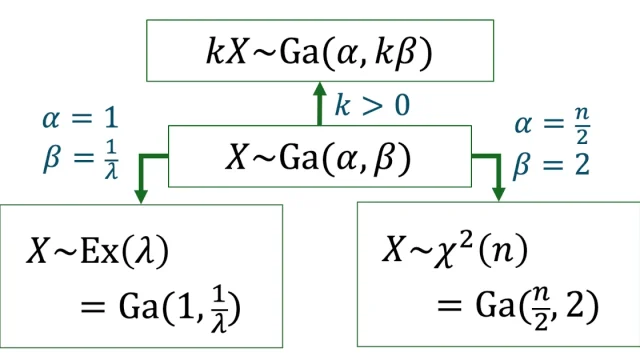 確率分布の性質
確率分布の性質 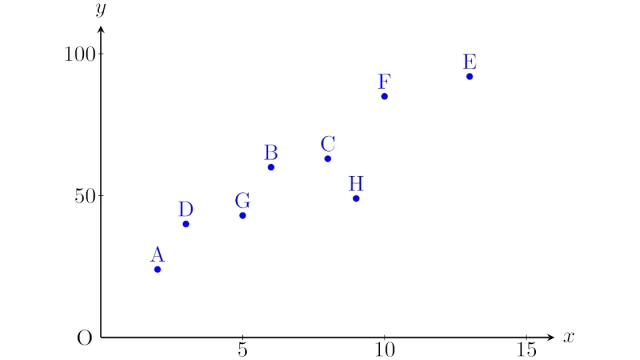 データの記述
データの記述 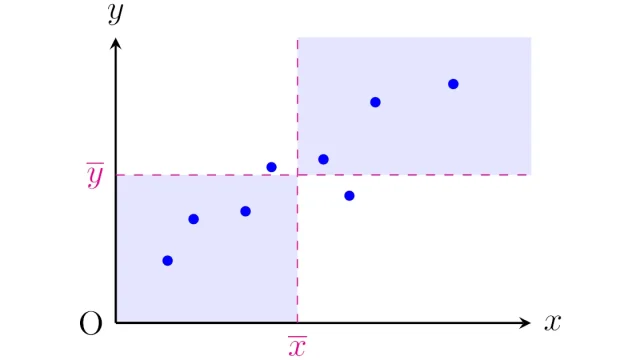 データの記述
データの記述