多くの理系大学生は1年次に線形代数学でベクトルを学び,微分積分学で偏微分を学びます.
数学や物理ではベクトルに関する微分を考えることがよくあり,このベクトルの微分を扱う分野としてベクトル解析があります.
その中でよく扱う微分作用素として,勾配$\operatorname{grad}$・発散$\operatorname{div}$・回転$\operatorname{rot}$($\operatorname{curl}$)があります.
また,これらはナブラ$\nabla$を用いることで便利に表すこともできます.
この記事では,
- 3つの微分作用素の定義とイメージ
- 3つの微分作用素のナブラ$\nabla$を用いた表し方
- 3つの微分作用素の合成の関係式
を順に説明します.
なお,3つの微分作用素の公式については以下の記事を参照してください.
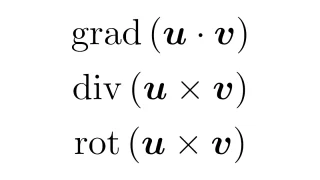
勾配gradの定義・具体例・図形的意味
まずは勾配$\operatorname{grad}$を定義します.
勾配gradの定義と図形的意味
変数は$\m{x}=(x_1,x_2,\dots,x_n)\in\R^n$とします.
各$x_i$について偏微分可能な関数$f:\R^n\to\R$に対して,
\begin{align*}\operatorname{grad}f(\m{x}):=\bmat{\pd{f}{x_1}(\m{x})\\\vdots\\\pd{f}{x_n}(\m{x})}\end{align*}
で$\operatorname{grad}f:\R^n\to\R^n$を定める.この$\operatorname{grad}f$を$f$の勾配(gradient)という.
第$i$変数$x_i$での偏微分は$x_i$軸方向の接線の傾きを表すのでしたから,$\operatorname{grad}f(\m{x})$は各軸方向の接線の傾きを書き並べたものということができます.
そのため,もし点$\m{a}$で$y=f(\m{x})$に接平面が存在すれば,$\operatorname{grad}f(\m{x})$は「接平面の最も急な傾きの方向」を表していることにもなります.
「点$\m{a}$で$y=f(\m{x})$に接平面が存在する」は「$f$が$\m{a}$で全微分可能である」ということもできますね.
勾配gradの具体例($f(x,y)=x^2+y^2$の勾配)
$n=2$のとき$f(x,y)=x^2+y^2$とすると,
\begin{align*}\operatorname{grad}f(x,y)
=\bmat{\pd{}{x}(x^2+y^2)\\\pd{}{y}(x^2+y^2)\\\pd{}{z}(x^2+y^2)}
=\bmat{2x\\2y}\end{align*}
となりますね.図示すると下図のようになります.
図のベクトルは見やすいように少し短く描いています.
確かに$z=f(x,y)=x^2+y^2$のグラフは$z$軸を軸とする放物面なので,各点での「接平面の最も急な傾きの方向」は原点と逆方向ですから,確かにその通りになっていますね.
発散divの定義・具体例・図形的意味
次に発散$\operatorname{div}$を定義します.
発散divの定義
変数は$\m{x}=(x_1,x_2,\dots,x_n)\in\R^n$とします.
各成分$x_i$について偏微分可能なベクトル値関数$\m{v}=\bmat{v_1\\\vdots\\v_n}:\R^n\to\R^n$に対して,
\begin{align*}\operatorname{div}\m{v}:=\pd{v_1}{x_1}+\dots+\pd{v_n}{x_n}\end{align*}
で$\operatorname{div}\m{v}:\R^n\to\R$を定め,これを$\m{v}$の発散(divergence)という.
つまり,ベクトル$\m{v}$の第$i$成分$v_i$を変数$x_i$で偏微分して足し合わせるわけですね.
発散divの具体例
$n=3$のとき$\m{v}(x,y,z)=\bmat{xy\\yz\\zx}$とすると,
\begin{align*}\operatorname{div}\m{v}(x,y,z)
&=\pd{}{x}(xy)+\pd{}{y}(yz)+\pd{}{z}(zx)
\\&=y+z+x\end{align*}
となりますね.
発散divの図形的意味
ベクトル値関数$\m{v}$は$\R^n$での(水や空気などの)「流れ」をイメージすると分かりやすいでしょう.
例えば,$n=2$のとき$\m{v}(x,y)=\bmat{v_1(x,y)\\v_2(x,y)}=\dfrac{1}{2}\bmat{x\\-y}$を考えると,例えば
- 点$(1,1)$での流れは$\m{v}(1,1)=\dfrac{1}{2}\bmat{1\\-1}$
- 点$(2,1)$での流れは$\m{v}(2,1)=\dfrac{1}{2}\bmat{2\\-1}$
- 点$(1,2)$での流れは$\m{v}(2,2)=\dfrac{1}{2}\bmat{2\\-2}$
- 点$(0,3)$での流れは$\m{v}(0,3)=\dfrac{1}{2}\bmat{0\\-3}$
ということになります.
このように点$(x,y)$での「流れ」を表しているのがベクトル値関数$\m{v}(x,y)$というわけですね.
$x$軸方向の流れの変化
さて,$\R^n$上のベクトル値関数$\m{v}$の第1成分$v_1$について,点$\m{a}=(a_1,a_2,\dots,a_n)$から点$\m{a}_h=(a_1+h,a_2,\dots,a_n)$に移動したときの変化の割合は
\begin{align*}\frac{v_1(\m{a}_h)-v_1(\m{a})}{h}\end{align*}
ですね.
ここで$h\to0$とすると点$\m{a}$での$x_1$軸方向の瞬間の増加が出てくるわけですが,これは
\begin{align*}\lim_{h\to0}\frac{v_1(\m{a}_h)-v_1(\m{a})}{h}=\pd{v_1}{x_1}(\m{a})\end{align*}
となりますね.
各軸方向の流れの変化の和
このように,ベクトル値関数$\m{v}$の$x_i$軸方向の増加を見たければ,$\displaystyle\pd{v_i}{x_i}$を考えればよいというわけですね.
つまり,「流れ」が点$\m{a}$を通過すると
- $x_1$方向に「流れ」が $\displaystyle\pd{v_1}{x_1}(\m{a})$増加
- $x_2$方向に「流れ」が $\displaystyle\pd{v_2}{x_2}(\m{a})$増加
- ……
- $x_n$方向に「流れ」が $\displaystyle\pd{v_n}{x_n}(\m{a})$増加
するというわけですね.よって,これらの和
\begin{align*}\operatorname{div}\m{v}(\m{a})=\pd{v_1}{x_1}(\m{a})+\pd{v_2}{x_2}(\m{a})+\dots+\pd{v_n}{x_n}(\m{a})\end{align*}
は点$\m{a}$での「増加する流れの量」を表していると言えますね.
よって,$\operatorname{div}\m{v}(\m{a})>0$なら点$\m{a}$で流れ量が多くなって(湧き出して)おり,$\operatorname{div}\m{v}(\m{a})>0$なら点$\m{a}$で流れの量が少なくなって(吸い込まれて)いるわけですね.
回転rotの定義・具体例・図形的意味
最後に回転$\operatorname{rot}$を定義します.
回転rotの定義
変数は$\m{x}=(x,y,z)\in\R^3$とします.
各成分$x$, $y$, $z$について偏微分可能なベクトル値関数$\m{v}=\bmat{u\\v\\w}:\R^3\to\R^3$に対して,
\begin{align*}\operatorname{rot}\m{v}:=\bmat{\pd{w}{y}-\pd{v}{z}\\\pd{u}{z}-\pd{w}{x}\\\pd{v}{x}-\pd{u}{y}}\end{align*}
で$\operatorname{rot}\m{v}:\R^3\to\R^3$を定め,これを$\m{v}$の回転(rotation, curl)という.$\operatorname{rot}\m{v}$は$\operatorname{curl}\m{v}$と表すこともある.
回転rotの具体例
$\m{v}(x,y,z)=\bmat{xy\\yz\\zx}$とすると,
\begin{align*}\operatorname{rot}\m{v}(x,y,z)
=\bmat{\pd{}{y}(zx)-\pd{}{z}(yz)\\\pd{}{z}(xy)-\pd{}{x}(zx)\\\pd{}{x}(yz)-\pd{}{y}(xy)}
=-\bmat{y\\z\\x}\end{align*}
となりますね.
回転rotの図形的意味
結論から言えば,この$\operatorname{rot}\m{v}$はベクトル値関数$\m{v}$が表す「流れ」の回転を表します.
このことについて,$\operatorname{rot}\m{v}$の第1成分
\begin{align*}\pd{w}{y}-\pd{v}{z}\end{align*}
がどういう意味で「流れ」の回転を表すのかを考えてみましょう.
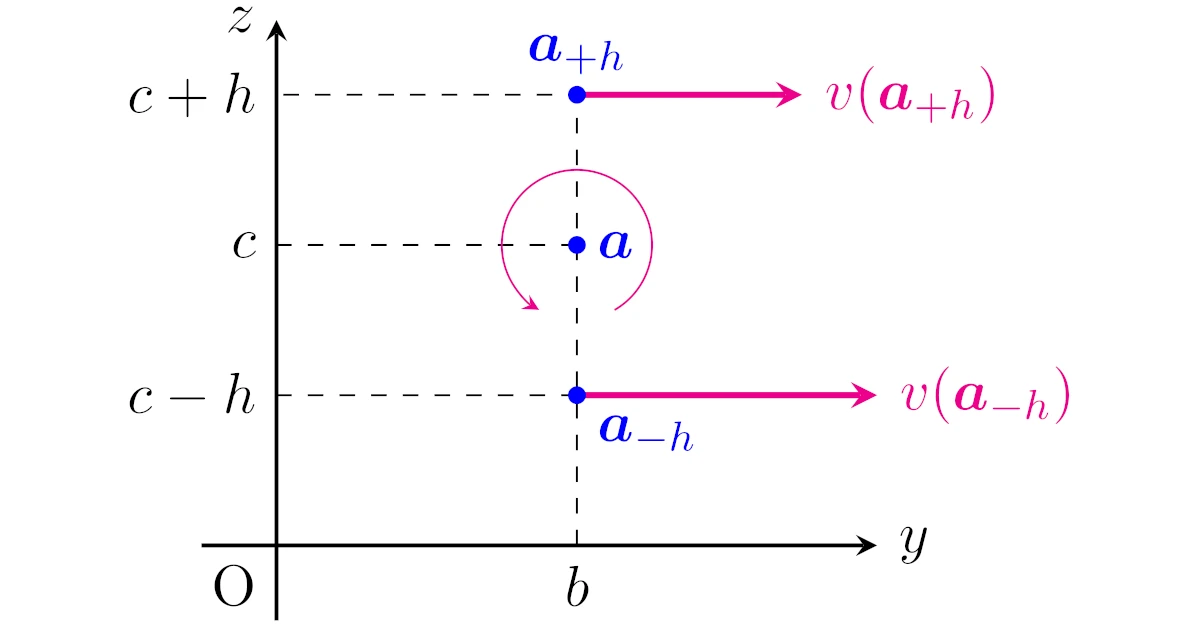
まずは点$\m{a}=(a,b,c)\in\R^3$を通る$x$軸に平行な直線の「上側」から$yz$平面を眺め,この直線の周りで$\m{v}$の「流れ」が正方向(反時計方向)にどれだけ回転しているかを考えます.
$y$軸方向の流れによる回転
2点
- $\m{a}_{+h}=(a,b,z+h)$
- $\m{a}_{-h}=(a,b,z-h)$
での$y$軸方向の「流れ」を比べると,$v(\m{a}_{-h})>v(\m{a}_{+h})$のときに正方向へ回転させるような「流れ」があると考えられますね.
よって,点$\m{a}_{+h}$から点$\m{a}_{-h}$へ移動したときの$y$軸方向の「流れ」の差の変化率は
\begin{align*}\frac{v(\m{a}_{-h})-v(\m{a}_{+h})}{2h}\end{align*}
ですね.
ここで$\operatorname{div}$と同じく$h\to0$とすると$y$軸方向の「流れ」による点$\m{a}$での瞬間の回転が出てくるわけですが,これは
\begin{align*}&\lim_{h\to0}\frac{v(\m{a}_{-h})-v(\m{a}_{+h})}{2h}
\\&=\lim_{h\to0}\brb{-\frac{1}{2}\bra{\frac{v(\m{a}_{+h})-v(\m{a})}{h}+\frac{v(\m{a}_{-h})-v(\m{a})}{-h}}}
\\&=-\frac{1}{2}\bra{\pd{v}{z}(\m{a})+\pd{v}{z}(\m{a})}
\\&=-\pd{v}{z}(\m{a})\end{align*}
となりますね.
$z$軸方向の流れによる回転
同様に,点$\m{a}’_{-h}:=(a,b-h,c)$と点$\m{a}’_{+h}:=(a,b+h,c)$の$y$軸方向の「流れ」を考えましょう.
このとき,$y$軸方向の「流れ」による点$\m{a}$での瞬間の回転は
\begin{align*}\lim_{h\to0}\frac{w(\m{a}’_{+h})-w(\m{a}’_{-h})}{2h}=\pd{w}{y}(\m{a})\end{align*}
となりますね.
rotのまとめ
以上より,
- $y$軸方向の流れにより生じる回転$-\displaystyle\pd{v}{z}(\m{a})$
- $z$軸方向の流れにより生じる回転$\displaystyle\pd{w}{y}(\m{a})$
の和$\displaystyle\pd{w}{y}(\m{a})-\displaystyle\pd{v}{z}(\m{a})$が点$\m{a}$での$x$軸に平行な回転軸周りの回転を表しているわけですね.
同じことを
- $y$軸に平行な回転軸周り
- $z$軸に平行な回転軸周り
でも考えて,
\begin{align*}\operatorname{rot}\m{v}:=\bmat{\pd{w}{y}-\pd{v}{z}\\\pd{u}{z}-\pd{w}{x}\\\pd{v}{x}-\pd{u}{y}}\end{align*}
の各成分が各軸に平行な回転軸周りの回転を表していることが分かりますね.
ナブラ∇を用いた表し方
ナブラ(nabla)$\nabla$を使うと,いまみた3つの微分作用素$\operatorname{grad}$, $\operatorname{div}$, $\operatorname{rot}$をスッキリ表すことができます.
変数$\m{x}=(x_1,\dots,x_n)$に関して,
\begin{align*}\nabla:=\bmat{\pd{}{x_1}\\\vdots\\\pd{}{x_n}}\end{align*}
と(形式的に)定める.
つまり,微分作用素$\pd{}{x_i}$を第$i$成分とする列ベクトルを$\nabla$と表すわけですね.
このとき,$\operatorname{grad}$, $\operatorname{div}$, $\operatorname{rot}$は形式的に
- $f:\R^n\to\R$に対して,
\begin{align*}\operatorname{grad}f
=\bmat{\pd{f}{x_1}\\\vdots\\\pd{f}{x_n}}
=\bmat{\pd{}{x_1}\\\vdots\\\pd{}{x_n}}f
=\nabla f.\end{align*} - $\m{v}:\R^n\to\R^n$に対して,
\begin{align*}\operatorname{div}\m{v}
=\pd{v_1}{x_1}+\dots+\pd{v_n}{x_n}
=\bmat{\pd{}{x_1}\\\vdots\\\pd{}{x_n}}\cdot\bmat{v_1\\\vdots\\v_n}
=\nabla\cdot\m{v}.\end{align*} - $\m{v}:\R^3\to\R^3$に対して,
\begin{align*}\operatorname{rot}\m{v}
=\bmat{\pd{w}{y}-\pd{v}{z}\\\pd{u}{z}-\pd{w}{x}\\\pd{v}{x}-\pd{u}{y}}
=\bmat{\pd{}{x}\\\pd{}{y}\\\pd{}{z}}\times\bmat{u\\v\\w}
=\nabla\times\m{v}.\end{align*}
となりますね.ここで,形式的に・は標準内積,$\times$は外積として考えています.
まとめると
- $\operatorname{grad}f=\nabla f$
- $\operatorname{div}\m{v}=\nabla\cdot\m{v}$
- $\operatorname{rot}\m{v}=\nabla\times\m{v}$
ですね.
$\operatorname{div}$の内積$\nabla\cdot\m{v}$はあくまで形式的なもので可換ではありません.$\m{v}\cdot\nabla$と書くと違う意味になってしまうので注意してください.
3つの微分作用素の合成
次に,いまみた3つの微分作用素を合成することを考えます.
ラプラシアン
ベクトル解析でよく現れる微分作用素にラプラシアンがあります.
同じ変数について2回偏微分可能な関数$f:\R^n\to\R$に対して
\begin{align*}\Delta f:=\operatorname{div}\operatorname{grad}f
\bra{=\ppd{f}{x_1}+\dots+\ppd{f}{x_n}}\end{align*}
と表し,この微分作用素$\Delta$をラプラシアン(Laplacian)という.
$\Delta f$は
\begin{align*}\Delta f=\nabla\cdot(\nabla f)\end{align*}
とも表せますね.
$C^2$級関数$f:\R^n\to\R$が
\begin{align*}\Delta f=0\end{align*}
を満たすとき,$f$を調和関数(harmonic function)という.
調和関数は性質の良い関数として,解析学でよく現れます.
3つの微分作用素の恒等式
いまみた3つの微分作用素の合成
- $\operatorname{rot}\operatorname{grad}$
- $\operatorname{div}\operatorname{rot}$
- $\operatorname{rot}\operatorname{rot}$
- $\operatorname{grad}\operatorname{div}$
について,以下が成り立ちます.
$C^2$級関数$f:\R^3\to\R$と$C^2$級ベクトル値関数$\m{v}=\bmat{u\\v\\w}:\R^3\to\R^3$に対して,以下が成り立つ.
- $\operatorname{rot}\operatorname{grad}f=\m{0}$
- $\operatorname{div}\operatorname{rot}\m{v}=0$
- $\operatorname{rot}\operatorname{rot}\m{v}=\operatorname{grad}\operatorname{div}\m{v}-\Delta\m{v}$
ただし,最後の等式の右辺の最後の項において$\Delta\m{v}:=\bmat{\Delta u\\\Delta v\\\Delta w}$である.
これらの等式は$\nabla$を使って以下のようにも表せますね.
- $\nabla\times(\nabla f)=\m{0}$
- $\nabla\cdot(\nabla\times\m{v})=0$
- $\nabla\times(\nabla\times\m{v})=\nabla(\nabla\cdot\m{v})-\Delta\m{v}$
$f$, $\m{v}$は$C^2$級だから2階までの偏微分は順序交換可能であることに注意すれば,以下のように計算により示すことができる.
$\operatorname{rot}\operatorname{grad}f=\m{0}$の証明
\begin{align*}\nabla\times(\nabla f)
=\nabla\times\bmat{\pd{f}{x}\\\pd{f}{y}\\\pd{f}{z}}
=\bmat{\ppdd{f}{y}{z}-\ppdd{f}{z}{y}\\\ppdd{f}{z}{x}-\ppdd{f}{x}{z}\\\ppdd{f}{x}{y}-\ppdd{f}{y}{x}}
=\m{0}\end{align*}
$\operatorname{div}\operatorname{rot}\m{v}=0$の証明
\begin{align*}&\nabla\cdot(\nabla\times\m{v})
=\nabla\cdot\bmat{\pd{w}{y}-\pd{v}{z}\\\pd{u}{z}-\pd{w}{x}\\\pd{v}{x}-\pd{u}{y}}
\\&=\pd{}{x}\bra{\pd{w}{y}-\pd{v}{z}}+\pd{}{y}\bra{\pd{u}{z}-\pd{w}{x}}+\pd{}{z}\bra{\pd{v}{x}-\pd{u}{y}}
\\&=\ppdd{w}{x}{y}-\ppdd{v}{x}{z}+\ppdd{u}{y}{z}-\ppdd{w}{y}{x}+\ppdd{v}{z}{x}-\ppdd{u}{z}{y}
\\&=\bra{\ppdd{u}{y}{z}-\ppdd{u}{z}{y}}+\bra{\ppdd{v}{z}{x}-\ppdd{v}{x}{z}}+\bra{\ppdd{w}{x}{y}-\ppdd{w}{y}{x}}=0\end{align*}
$\operatorname{rot}\operatorname{rot}\m{v}=\operatorname{grad}\operatorname{div}\m{v}-\Delta\m{v}$の証明
\begin{align*}&\nabla\times(\nabla\times\m{v})
=\nabla\times\bmat{\pd{w}{y}-\pd{v}{z}\\\pd{u}{z}-\pd{w}{x}\\\pd{v}{x}-\pd{u}{y}}
\\&=\bmat{\pd{}{y}\bigl(\pd{v}{x}-\pd{u}{y}\bigr)-\pd{}{z}\bigl(\pd{u}{z}-\pd{w}{x}\bigr)\\
\pd{}{z}\bigl(\pd{w}{y}-\pd{v}{z}\bigr)-\pd{}{x}\bigl(\pd{v}{x}-\pd{u}{y}\bigr)\\
\pd{}{x}\bigl(\pd{u}{z}-\pd{w}{x}\bigr)-\pd{}{y}\bigl(\pd{w}{y}-\pd{v}{z}\bigr)}
\\&=\bmat{\bigl(\ppdd{v}{y}{x}+\ppdd{w}{z}{x}\bigr)-\bigl(\ppd{u}{y}+\ppd{u}{z}\bigr)\\
\bigl(\ppdd{w}{z}{y}+\ppdd{u}{x}{y}\bigr)-\bigl(\ppd{v}{x}+\ppd{v}{z}\bigr)\\
\bigl(\ppdd{u}{x}{z}+\ppdd{v}{y}{z}\bigr)-\bigl(\ppd{w}{x}+\ppd{w}{y}\bigr)}
\\&=\bmat{\pd{}{x}\bigl(\pd{u}{x}+\pd{v}{y}+\pd{w}{z}\bigr)-\bigl(\ppd{u}{x}+\ppd{u}{y}+\ppd{u}{z}\bigr)\\
\pd{}{y}\bigl(\pd{u}{x}+\pd{v}{y}+\pd{w}{z}\bigr)-\bigl(\ppd{v}{x}+\ppd{v}{y}+\ppd{v}{z}\bigr)\\
\pd{}{z}\bigl(\pd{w}{x}+\pd{w}{y}+\pd{w}{z}\bigr)-\bigl(\ppd{w}{x}+\ppd{w}{y}+\ppd{w}{z}\bigr)}
\\&=\bmat{\pd{}{x}\bigl(\pd{u}{x}+\pd{v}{y}+\pd{w}{z}\bigr)\\
\pd{}{y}\bigl(\pd{u}{x}+\pd{v}{y}+\pd{w}{z}\bigr)\\
\pd{}{z}\bigl(\pd{u}{x}+\pd{v}{y}+\pd{w}{z}\bigr)}
-\bmat{\ppd{u}{x}+\ppd{u}{y}+\ppd{u}{z}\\\ppd{v}{x}+\ppd{v}{y}+\ppd{v}{z}\\\ppd{w}{x}+\ppd{w}{y}+\ppd{w}{z}}
\\&=\nabla\bra{\pd{u}{x}+\pd{v}{y}+\pd{w}{z}}-\bmat{\Delta u\\\Delta v\\\Delta w}
\\&=\nabla(\nabla\cdot\m{v})-\Delta\m{v}\end{align*}

コメント