 線形代数学
線形代数学 正方行列が正則であるための4つの必要十分条件を整理する
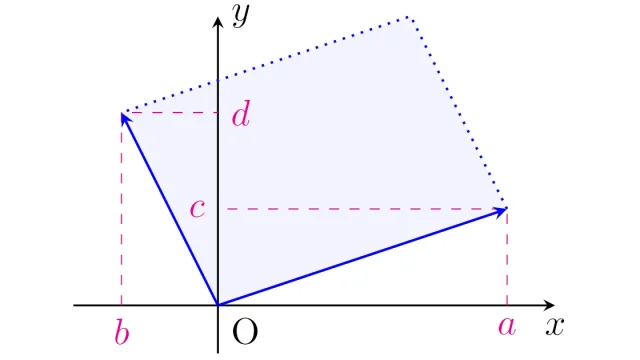
正則行列はさまざまな「よい性質」をもち頻繁に現れるため,正則性の判定ができることは大切です.この記事では,正方行列が正則であるための,ランク・連立1次方程式・線形独立性・行列式による必要十分条件を整理します.
 線形代数学
線形代数学 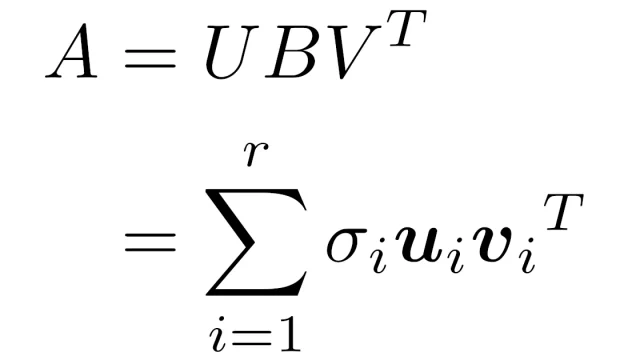 線形代数学
線形代数学 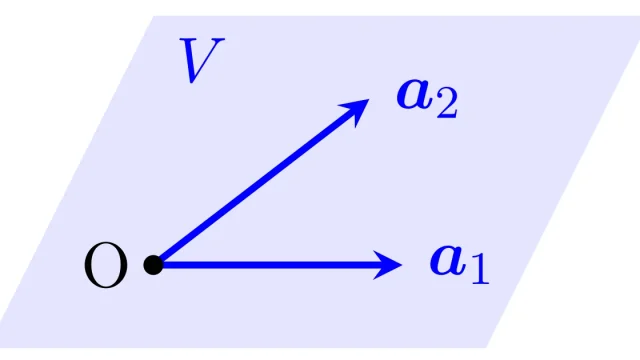 線形空間の基本
線形空間の基本 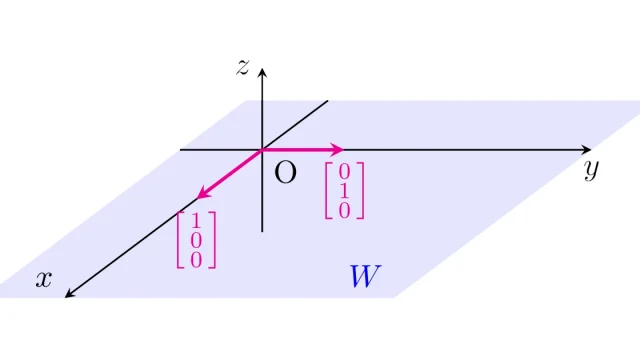 線形空間の基本
線形空間の基本 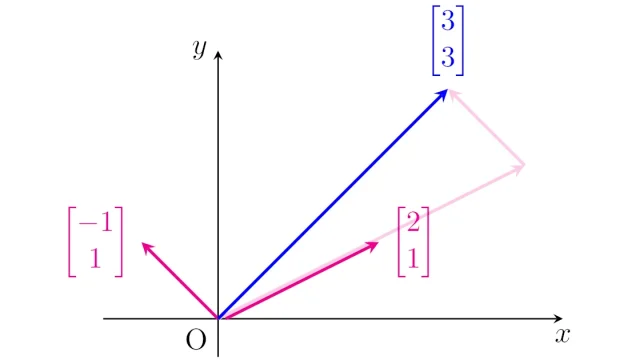 線形空間の基本
線形空間の基本 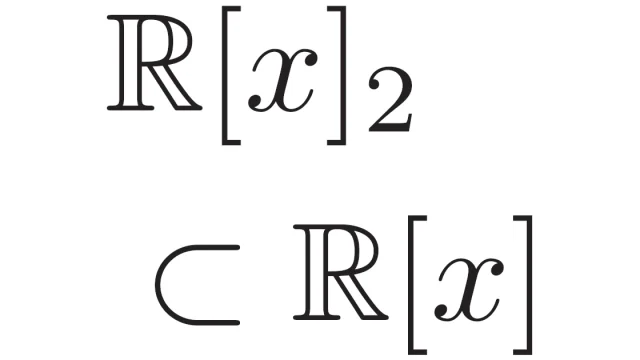 線形空間の基本
線形空間の基本 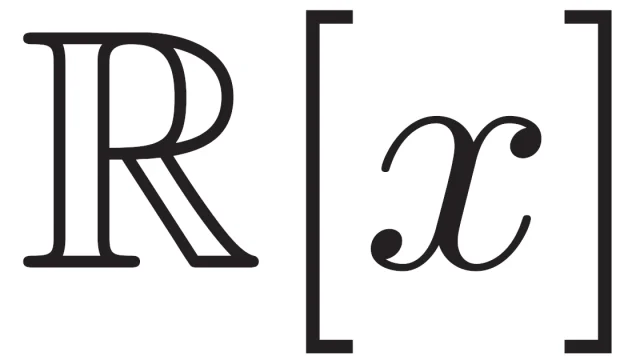 線形空間の基本
線形空間の基本 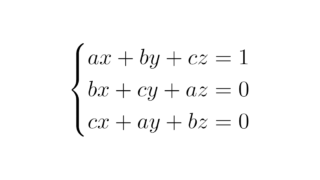 線形代数学
線形代数学 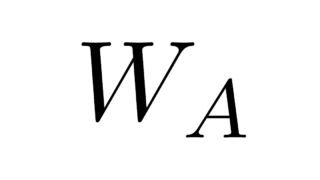 線形代数学の基本
線形代数学の基本 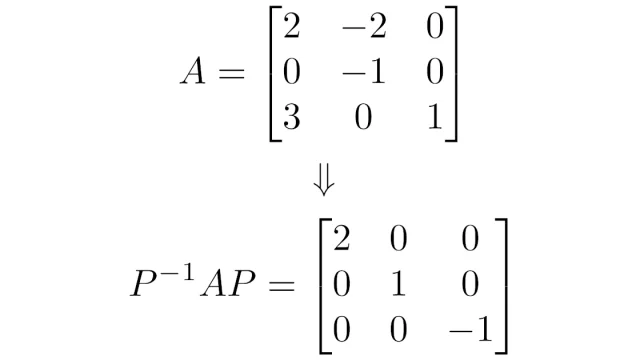 線形代数学の基本
線形代数学の基本