 常微分方程式
常微分方程式 解ける常微分方程式2|1階線形・ベルヌーイ型の解法と具体例
解ける常微分方程式の中でも「1階線形」は非常によく現れるもののひとつです.「ベルヌーイの微分方程式」は変形を施すことで1階線形に帰着する常微分方程式としてよく現れるので,ベルヌーイの微分方程式の解法も併せて理解しておきましょう.
 常微分方程式
常微分方程式 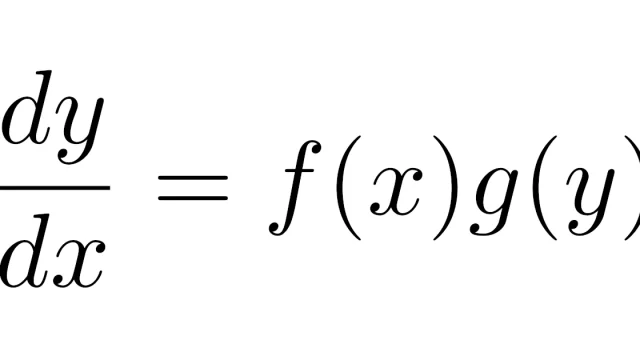 常微分方程式
常微分方程式 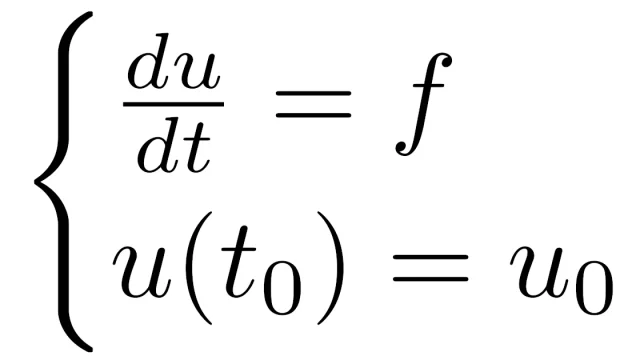 常微分方程式
常微分方程式 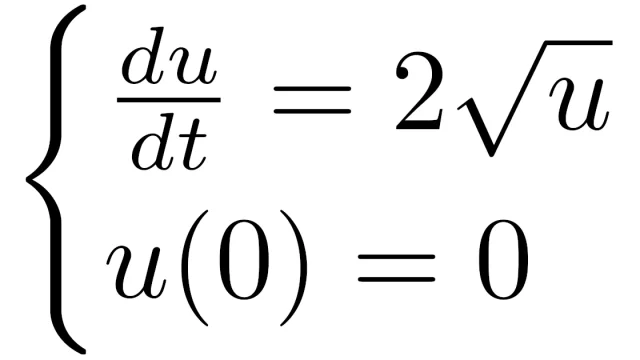 常微分方程式
常微分方程式 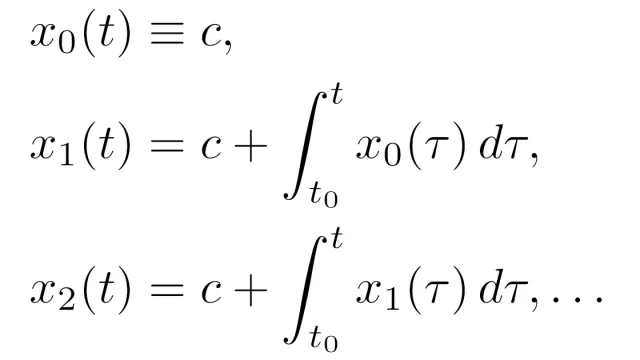 常微分方程式
常微分方程式