最尤推定法・尤度関数の直感的な考え方｜データから分布を推定

何らかの全国規模の調査を行いたいとき，対象者全員に調査することができれば最もよいですが，それは時間やコストなどの面から現実的ではありません．

そのため，実際には対象者の一部に調査を行い，そこで得られたデータから対象者全員の分布を推測することになります．

その推測の方法は色々ありますが，ひとつに最尤(さいゆう)推定法というものがあり，名前の通り「最もそれっぽい（尤(もっと)もらしい）分布を推定する方法」です．

「最尤推定法」という名前を聞くといかめしい印象を受けるかもしれませんが，考え方自体はシンプルでそれほど難しいものではありません．

この記事では

最尤推定法の考え方
最尤推定法の具体例
尤度関数と対数尤度関数

を順に説明します．

スクロールできます

最尤推定法の考え方
1. 分布を推定するとは？
2. 最尤推定法の考え方
正規分布の最尤推定法

最尤推定法の考え方

最尤推定法を使う際には，最初に

どのような分布に従うのか
実際に得られたデータ

の２つを用意します．例えば，「全国の成人男性の身長」を最尤推定法で考える際には

全国の成人男性の身長は「正規分布」に従う
1000人の成人男性の身長のデータ

などが既に分かっているものとします．この２つから「全国の成人男性の身長」がどのように分布しているかを推定するわけですね．

ここからしばらく次の問題を考えましょう．

ある正規分布から６個のデータ $4.4$ , $5.3$ , $5.2$ , $5.7$ , $4.7$ , $4.1$ が得られた．このときの正規分布を最尤推定法により推定せよ．

最尤推定法で考える分布は一般には正規分布とは限りませんが，正規分布でなくても考え方は同じなので，この記事では正規分布で考えます．

分布を推定するとは？

「正規分布を推定する」とはどういうことでしょうか？

正規分布は（確率密度関数が）下図のような山のような形をしたグラフで表される分布でした．

ただし，「正規分布」と一言で言っても，グラフの

裾の広がり方（分散）
真ん中の位置（平均）

に特徴が表れます．例えば，なだらかな（分散が大きい）正規分布のグラフ

になることもありますし，山の頂上の $x$ が $0$ でない（平均が $0$ でない）正規分布のグラフ

になることもあります．

よって，分布を推定するとは「このような色々な分布の中で，どれが最もそれっぽい正規分布なのかを推定しよう」ということなわけです．

正規分布の平均と分散のように，分布の特徴を示すものをパラメーターと言うことも多いですね．

最尤推定法の考え方

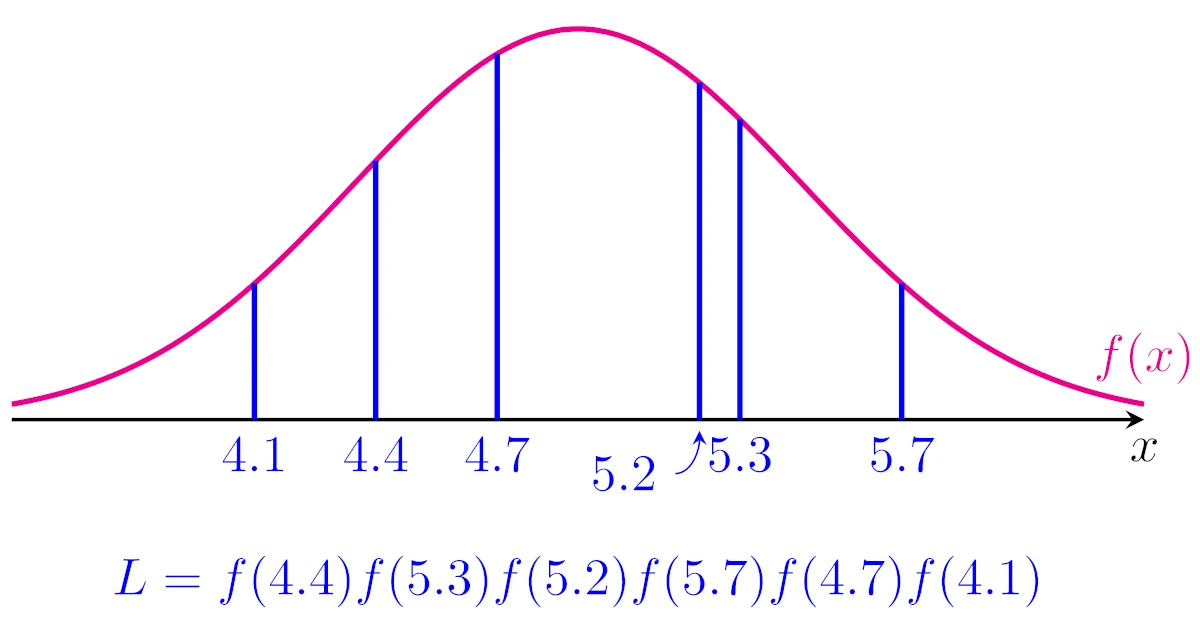
ここで，問題の６個のデータ $4.4$ , $5.3$ , $5.2$ , $5.7$ , $4.7$ , $4.1$ を数直線上に図示すると下図のようになります．

さらに，このデータが正規分布に従うことが分かっているとします．

このとき，「どんな正規分布だと思いますか？」と聞くと，多くの人は以下のようなグラフを描くのではないでしょうか？

一方，多くのデータが集まっているところからずれたグラフ

はなさそうですし，あまりに集中しすぎたグラフ

もなさそうです．つまり，「データがあるところの値が出来るだけ大きくなるような分布がそれっぽい」ということになります．

したがって，正規分布の確率密度関数を $f$ とし，６個のデータ $4.4$ , $5.3$ , $5.2$ , $5.7$ , $4.7$ , $4.1$ を $f$ に代入して掛け合わせた

$\begin{align*}L=f(4.4)f(5.3)f(5.2)f(5.7)f(4.7)f(4.1)\end{align*}$

が最大になるような確率密度関数 $f$ をもつ分布が，最もそれっぽい正規分布ということができますね．

いまは暗にデータが独立に正規分布に従うことを仮定しているので積になっていますが，独立とは限らない場合は同時確率密度関数となります．

要するに「下図の青線の長さの積が最大になる $f (x)$ が最もそれっぽい $f (x)$ である」という考え方ですね．

このような考え方に基づく分布の推定方法を最尤推定法といいます．

スクロールできます

正規分布の最尤推定法

以上が最尤推定法の考え方で，次はいま考えたことを一般化することを考えましょう．

最尤推定法の要は尤度関数

ある分布に独立に従う $n$ 個のデータ $x_{1}, x_{2}, \dots, x_{n}$ に対して，この分布の確率密度関数を $f$ とするとき，

$\begin{align*}L=\prod_{k=1}^{n}f(x_k)\end{align*}$

を尤度(ゆうど)関数（likelihood function）といい，尤度関数が最大となる $f$ を求めることにより分布を推定する方法を最尤推定法（method of maximum likelihood estimation）という．

上の尤度関数 $L$ の定義における $\prod_{k = 1}^{n}$ は $\sum_{k = 1}^{n}$ の掛け算バージョンです．つまり，

$\begin{align*}L=f(x_1)\times f(x_2)\times\dots\times f(x_n)\end{align*}$

です．なお， $Π$ はギリシャ文字 $π$ の大文字で「パイ」と読みます．

先ほども書きましたが，最尤推定法を考えるときには，もともと

データ $x_{1}, x_{2}, \dots, x_{n}$
分布の確率密度関数 $f$

が用意されていることが大切です．

具体的に正規分布で考えましょう．平均 $μ$ ，分散 $σ$ の正規分布の確率密度関数 $f_{μ, σ}$ は

$\begin{align*}f_{\mu,\sigma}(x)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\end{align*}$

と表されるのでしたから，この関数 $f_{μ, σ}$ に $n$ 個のデータ $x_{1}, x_{2}, \dots, x_{n}$ を代入して掛け合わせた

$\begin{align*}L(\mu,\sigma) &=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x_1-\mu)^2}{2\sigma^2}}\times\dots\times\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x_n-\mu)^2}{2\sigma^2}} \\&=\bra{\frac{1}{\sqrt{2\pi\sigma^2}}}^{n}e^{-\frac{(x_1-\mu)^2}{2\sigma^2}}e^{-\frac{(x_2-\mu)^2}{2\sigma^2}}\dots e^{-\frac{(x_n-\mu)^2}{2\sigma^2}} \\&=(2\pi\sigma^2)^{-\frac{n}{2}}e^{-\frac{1}{2\sigma^2}\brb{(x_1-\mu)^2+\dots+(x_n-\mu)^2}}\end{align*}$

を尤度関数と言うわけですね．

先ほど説明したように正規分布の「位置」と「形」はそれぞれ平均 $μ$ と分散 $σ$ によって決まります．

よって，正規分布の最尤推定法では尤度関数 $L (μ, σ)$ を最大にする $μ$ と $σ$ を求めることにより，最も尤もらしい正規分布を推定するということになります．

微分しやすい対数尤度関数

さて，それでは実際にどうすれば尤度関数 $L (μ, σ)$ が最大となるような $μ$ と $σ$ を求めることができるのでしょうか？

関数の最大，最小を求める問題では微分を用いるのがよくある方法ですが，尤度関数 $L (μ, σ)$ は積の形で表されているので微分すると式がやや煩雑になります．

そこで，尤度関数 $L$ に自然対数をとった対数尤度関数を用いるとスッキリすることがよくあります．

尤度関数 $L$ に自然対数をとってできた関数

$\begin{align*}\log{L}=\sum_{k=1}^{n}\log{f(x_k)}\end{align*}$

対数尤度関数 (log-likelihood function)という．

積に $\log$ をとると和に変わるのでした（ $\log a b = \log a + \log b$ ）から，尤度関数

$\begin{align*}L=f(x_1)\times f(x_2)\times\dots\times f(x_n)\end{align*}$

の両辺で自然対数 $\log$ をとれば

$\begin{align*}\log{L}=\log{f(x_1)}+\log{f(x_2)}+\dots+\log{f(x_n)}\end{align*}$

となるわけですね．これを $\sum$ を用いて表したものが上の定義式ですね．

$\log$ は単調増加関数なので，尤度関数 $L$ が最大になるとき対数尤度関数 $\log L$ も最大になります．

よって，平均 $μ$ ，分散 $σ$ の正規分布の尤度関数 $L (μ, σ)$ を最大にするような $μ$ と $σ$ を求めたければ，対数尤度関数 $\log L (μ, σ)$ を最大にするような $μ$ と $σ$ を求めればよいことになります．

積のまま微分すると式は煩雑になりますが，和の微分は各項で微分ができるので式はそれほど煩雑になりません．対数をとって和の形にしたのはこの理由からです．

平均 $μ$ ，分散 $σ$ の正規分布の対数尤度関数は

$\begin{align*}M(\mu,\sigma) &=\log{L}(\mu,\sigma) \\&=\log{\brc{(2\pi\sigma^2)^{-\frac{n}{2}}e^{-\frac{1}{2\sigma^2}\brb{(x_1-\mu)^2+\dots+(x_n-\mu)^2}}}} \\&=-\frac{n}{2}\log{2\pi}-n\log{\sigma}-\frac{(x_1-\mu)^2+\dots+(x_n-\mu)^2}{2\sigma^2}\end{align*}$

となりますね．

微分して極値を求める

上述したように，微分を用いることで対数尤度関数を $M (μ, σ) := \log L (μ, σ)$ とおき， $M$ の最大値を求めましょう．

一般に微分可能な２変数関数 $f$ に対して， $\frac{\partial f}{\partial x} (a, b) = \frac{\partial f}{\partial y} (a, b) = 0$ を満たす $(a, b)$ が $f (x, y)$ を最大（最小）にする $(x, y)$ の候補です．

実際，正規分布の対数尤度関数の場合には

$\begin{align*}\pd{M}{\mu}(\mu,\sigma)=\pd{M}{\sigma}(\mu,\sigma)=0\end{align*}$

を満たすような $(μ, σ)$ で $M (μ, σ)$ は最大となります．

$\begin{align*} & \pd{M}{\mu}(\mu,\sigma)=0 \\\iff& -\frac{2(\mu-x_1)+\dots+2(\mu-x_n)}{2\sigma^2}=0 \\\iff& (\mu-x_1)+\dots+(\mu-x_n)=0 \\\iff& \mu=\frac{x_1+\dots+x_n}{n}, \\& \pd{M}{\sigma}(\mu,\sigma)=0 \\\iff& -\frac{n}{\sigma}+\frac{(x_1-\mu)^2+\dots+(x_n-\mu)^2}{\sigma^3}=0 \\\iff& (x_1-\mu)^2+\dots+(x_n-\mu)^2=n\sigma^2 \\\iff& \sigma^2=\frac{(x_1-\mu)^2+\dots+(x_n-\mu)^2}{n} \end{align*}$

となるので，

$μ = \frac{x_{1} + \dots + x_{n}}{n}$
$σ^{2} = \frac{(x_{1} - μ)^{2} + \dots + (x_{n} - μ)^{2}}{n}$

のとき $M (μ, σ)$ が最大，すなわち， $L (μ, σ)$ が最大となります．

対数尤度関数を用いなくても，頑張って尤度関数を微分しても全く同じ結論が得られます．

結論

さて，ただ「正規分布に従う $n$ 個のデータを用意し，その尤度関数が最大になるような組 $(μ, σ)$ を求めよう」と求めたわけですが，今求まった $μ$ と $σ^{2}$ に見覚えはありませんか？

$μ = \frac{x_{1} + \dots + x_{n}}{n}$ はデータ $x_{1}, \dots, x_{n}$ の平均
$σ^{2} = \frac{(x_{1} - μ)^{2} + \dots + (x_{n} - μ)^{2}}{n}$ はデータ $x_{1}, \dots, x_{n}$ の分散