常微分方程式はいつでも解を明示的に求められるとは限りませんが,解けることがよく知られている常微分方程式もいくつかあり,そのような常微分方程式を解けるようになっておくことは大切です.
解ける常微分方程式の中でも変数分離形は最も基本的なもののひとつです.
また,変形を施すことで変数分離形に帰着する同次形の常微分方程式の解法も併せて解説します.
この記事では
- 変数分離形の常微分方程式とその解法
- 具体的に変数分離形の常微分方程式を解く
- 変数分離形に帰着させる同次形の常微分方程式
を順に解説します.
変数分離形の常微分方程式とその解法
未知関数$y$,変数$x$の
\begin{align*}y'(x)=(\text{$x$の式})\times(\text{$y(x)$の式})\end{align*}
の形をした常微分方程式を変数分離形といいます.
1変数関数の微分方程式は一般に常微分方程式と呼ばれますね.
$(\text{$x$の式})$の部分を$f(x)$と書き,$(\text{$y(x)$の式})$の部分を$g(y(x))$と書いて,
\begin{align*}y'(x)=f(x)g(y(x))\end{align*}
などと表すことも多いです.
変数分離形の常微分方程式の具体例
例えば,次の常微分方程式はいずれも変数分離形です.
- $y'(x)=2x+1$
- $y'(x)=y(x)^2$
- $y'(x)=\frac{x(y(x)-1)}{x^2+1}$
- $y'(x)=3x^2(y(x)^2-1)$
$f$, $g$は定数関数であってもよく,1つ目と2つ目の常微分方程式も変数分離形といえることに注意しましょう.
のちに実際にこれらの微分方程式を解きますが,まずは一般的な解法を見ておきましょう.
変数分離形の常微分方程式の解法
ここでは変数分離形の常微分方程式$y'(x)=f(x)g(y(x))$の解き方を解説します.ただし,関数$g$は局所リプシッツ連続かつ右辺は$(x,y)$に関して連続であるとします.
- 定数関数の解$y$を求める
- 定数関数でない解$y$を求める
の2パターンの解があるので,これらを順に求めます.
連続性の仮定により,常微分方程式の初期値問題の解が一意に存在します.理論にこだわらない場合は,この記事では特に気にする必要はありません.
ケース1:定数関数の解$y$を求める
$g(k)=0$を満たす実数$k$が存在するときには,恒等的に値$k$をとる定数関数$y(x)\equiv k$が1つの解です.
実際,$y(x)\equiv k$なら$y'(x)\equiv0$なので微分方程式の両辺とも恒等的に値0をとり,定数関数$y(x)\equiv k$は解であることが分かりますね.
一方,$g(k)\neq0$なる実数$k$に対して,定数関数$y(x)\equiv k$は解になりません.
ケース2:定数関数でない解$y$を求める
定数関数でない解$y(x)$は$g(y(x))\neq0$を満たすので,両辺を$g(y(x))$で割って
\begin{align*}\frac{1}{g(y(x))}y'(x)=f(x)
\iff\frac{1}{g(y(x))}\cdot\frac{dy}{dx}(x)=f(x)\end{align*}
となります.さらに両辺を$g(y(x))$で割り,$x$で積分すると
\begin{align*}\int\frac{1}{g(y(x))}\cdot\frac{dy}{dx}(x)\,dx=\int f(x)\,dx
\iff\int\frac{1}{g(y)}\,dy=\int f(x)\,dx\end{align*}
となります.左辺では(形式的には約分されたように見えますが,)$y(x)$が定数関数でないことより置換積分をしています.
最後の等式の両辺を計算すれば,導関数がなくなっており微分方程式が解けています.
実は最初の「定数関数でない解$y$は$g(y(x))\neq0$を満たす」のところで,次のように初期値問題の解の一意存在性を用いています:
もし2つの解$y_1$と$y_2$がある$x$で一致したとすると,$y_1$も$y_2$も同じ初期条件の解であることになり,初期値問題の解の一意性から$y_1$と$y_2$は等しい解であることが分かります.ケース1より$g(k)=0$を満たす実数$k$に対して定数関数$y(x)\equiv k$が解となるのでしたから,定数関数でない解$y(x)$は値$k$をとらないので$g(y(x))\neq0$が成り立つというわけですね.
具体的に変数分離形の常微分方程式を解く
ここで,上で挙げた4つの常微分方程式を解きましょう.
具体例1:$y'(x)=2x+1$を解く
常微分方程式$y'(x)=2x+1$を解け.
分類的には$f(x)=2x+1$, $g(y)\equiv1$の変数分離形ですが,$y'(x)$が明示的に得られているわけですから単に両辺を$x$で積分すればよいですね.
常微分方程式の両辺を$x$で積分して,
\begin{align*}y(x)=x^2+x+C\end{align*}
と解ける.ただし,$C$は任意定数である.
具体例2:$y'(x)=y(x)^2$を解く
常微分方程式$y'(x)=y(x)^2$を解け.
$f(x)\equiv1$, $g(y)=y^2$の変数分離形です.$k$の方程式$g(k)=0$は解をもつので,定数関数解が存在します.
$g(k)=k^2$とおくと,$k$の方程式$g(k)=0$は
\begin{align*}g(k)=0\iff k^2=0\iff k=0\end{align*}
と解けるから,定数関数$y(x)\equiv0$は解の1つである.
また,定数関数でない解$y(x)$は(初期値問題の一意性より)値0をとらないので,両辺を$y(x)^2$で割って$x$で積分すると
\begin{align*}&\int \frac{1}{y(x)^2}\frac{dy}{dx}(x)\,dx=\int\,dx
\\&\iff\int \frac{1}{y^2}\,dy=\int\,dx
\\&\iff-\frac{1}{y(x)}=x+C
\\&\iff y(x)=-\frac{1}{x+C}\end{align*}
と解ける.ただし,$C$は任意定数である.以上より,解は
\begin{align*}y(x)\equiv0,\quad
y(x)=-\frac{1}{x+C}\end{align*}
である.
解$y(x)=-\frac{1}{x+C}$は$x=-C$で発散する解です.このような,ある点で発散する解を爆発解(blow-up solution)といいます.
具体例3:$y'(x)=\frac{x(y(x)-1)}{x^2+1}$を解く
常微分方程式$y'(x)=\frac{x(y(x)-1)}{x^2+1}$を解け.
$f(x)=\frac{x}{x^2+1}$, $g(y)=y-1$の変数分離形です.具体例2と同じく定数関数解が存在しますが,一般解に含めることができます.
$g(k)=k-1$とおくと,$k$の方程式$g(k)=0$は
\begin{align*}g(k)=0\iff k-1=0\iff k=1\end{align*}
と解けるから,定数関数$y(x)\equiv1$は解の1つである.
また,定数関数でない解$y(x)$は(初期値問題の一意性より)値1をとらないので,両辺を$y(x)-1$で割って$x$で積分すると
\begin{align*}&\int \frac{1}{y(x)-1}\frac{dy}{dx}(x)\,dx=\int\frac{x}{x^2+1}\,dx
\\&\iff\int \frac{1}{y-1}\,dy=\frac{1}{2}\log{(x^2+1)}+C
\\&\iff\log{|y(x)-1|}=\log{(e^C\sqrt{x^2+1})}
\\&\iff y(x)=1\pm e^C\sqrt{x^2+1}\end{align*}
と解ける.ただし,$C$は任意定数である.
定数関数解$y(x)\equiv1$が$y(x)=1+0\sqrt{x^2+1}$とも表せることに注意すると,解は
\begin{align*}y(x)=1+D\sqrt{x^2+1}\end{align*}
である.ただし,$D$は任意定数である.
$C$は任意の実定数にとれるので,$e^C$は任意の正定数,$-e^C$は任意の負定数にとれます.さらに定数関数解$y(x)\equiv1$とも併せれば,ひとつの式にまとめられるわけですね.
具体例2と同様に$y(x)\equiv1$, $y(x)=1+D\sqrt{x^2+1}$($D$は0でない定数)と答えても間違いではありませんが,まとめられるときはまとめておくのがよいでしょう.
具体例4:$y'(x)=3x^2(y(x)^2-1)$を解く
常微分方程式$y'(x)=3x^2(y(x)^2-1)$を解け.
$f(x)=3x^2$, $g(y)=y^2-1$の変数分離形です.今回は定数関数解が2つ現れ,片方のみ一般解に含めることができます.
$g(k)=k^2-1$とおくと,$k$の方程式$g(k)=0$は
\begin{align*}g(k)=0\iff k^2-1=0\iff k=\pm1\end{align*}
と解けるから,2つの定数関数$y(x)\equiv\pm1$は解である.
また,定数関数でない解$y(x)$は(初期値問題の一意性より)値1と値−1をとらないので,両辺を$y(x)^2-1$で割って$x$で積分すると
\begin{align*}&\int \frac{1}{y(x)^2-1}\frac{dy}{dx}(x)\,dx=\int 3x^2\,dx
\\&\iff\frac{1}{2}\int\bra{\frac{1}{y-1}-\frac{1}{y+1}}\,dy=\int 3x^2\,dx
\\&\iff\frac{1}{2}\log{\abs{\frac{y(x)-1}{y(x)+1}}}=x^3+C
\\&\iff\abs{\frac{y(x)-1}{y(x)+1}}=e^{2x^3+2C}
\\&\iff\frac{y(x)-1}{y(x)+1}=\pm e^Ce^{2x^3}
\\&\iff y(x)=\frac{1\pm e^Ce^{2x^3}}{1-(\pm e^C)e^{2x^3}}\end{align*}
と解ける.ただし,$C$は任意定数で,最後の等式は複号同順である.
定数関数解$y(x)\equiv1$が$y(x)=\frac{1+0e^{2x^3}}{1-0e^{2x^3}}$とも表せることに注意すると,解は
\begin{align*}y(x)\equiv-1,\quad
y(x)=\frac{1+De^{2x^3}}{1-De^{2x^3}}\end{align*}
である.ただし,$D$は任意定数である.
定数関数解$y(x)\equiv1$は$y(x)=\frac{1+De^{2x^3}}{1-De^{2x^3}}$にまとめられますが,$y(x)\equiv-1$はまとめられないので分けて書くことになります.
変数分離形に帰着させる同次形の常微分方程式
未知関数$y$,変数$x$の
\begin{align*}y'(x)=f\bra{\frac{y(x)}{x}}\end{align*}
の形をした常微分方程式を同次形といい,$u(x)=\frac{y(x)}{x}$と新しい関数$u$をおくことで,未知関数$u$の変数分離形の常微分方程式に帰着させることができます.
具体例1:$y'(x)=\frac{y(x)^2-xy(x)}{x^2}-3$を解く
常微分方程式$y'(x)=\frac{y(x)^2-xy(x)}{x^2}-3$を解け.
問題の常微分方程式は$y'(x)=(\frac{y(x)}{x})^2-\frac{y(x)}{x}-3$と変形できる.未知関数$u$を$u(x)=\frac{y(x)}{x}$で定めると,$xu(x)=y(x)$なので両辺を$x$で微分して
\begin{align*}u(x)+xu'(x)=y'(x)\end{align*}
が成り立つ.よって,常微分方程式は
\begin{align*}&u(x)+xu'(x)=u(x)^2-u(x)-3
\\&\iff xu'(x)=u(x)^2-2u(x)-3
\\&\iff u'(x)=\frac{(u(x)-3)(u(x)+1)}{x}\end{align*}
と変形できる.定数関数$u(x)\equiv3,-1$はいずれも解で,他に定数関数解は存在しない.
また,定数関数でない解$u(x)$は(初期値問題の一意性より)値3と値−1をとらないので,両辺を$(u(x)-3)(u(x)+1)$で割って$x$で積分すると
\begin{align*}&\iff\frac{1}{4}\int\bra{\frac{1}{u-3}-\frac{1}{u+1}}\,du=\int \frac{1}{x}\,dx
\\&\iff\frac{1}{4}\log{\abs{\frac{u(x)-3}{u(x)+1}}}=\log{|x|}+C
\\&\iff\abs{\frac{u(x)-3}{u(x)+1}}=e^{4C}x^4
\\&\iff u(x)=\frac{3\pm e^{4C}x^4}{1-(\pm e^{4C})x^4}\end{align*}
と解ける.ただし,$C$は任意定数で,最後の等式は複号同順である.
定数関数解$u(x)\equiv3$が$u(x)=\frac{3+0x^4}{1-0x^4}$とも表せることに注意すると,解$u(x)$は
\begin{align*}u(x)\equiv-1,\quad
u(x)=\frac{3+Dx^4}{1-Dx^4}\end{align*}
である.ただし,$D$は任意定数である.$xu(x)=y(x)$より,解$y(x)$は
\begin{align*}y(x)=-x,\quad
y(x)=\frac{(3+Dx^4)x}{1-Dx^4}\end{align*}
である.
$u$の常微分方程式に書き換えた$u'(x)=\frac{u(x)^2-2u(x)-3}{x}$が変数分離形になっている点がポイントです.
具体例2:$y'(x)=\frac{3x+5y(x)}{x-y(x)}$を解く
未知関数$y$,変数$x$の
\begin{align*}y'(x)=\frac{ax+by(x)}{Ax+By(x)}\quad(aB-Ab\neq0)\end{align*}
の形をした常微分方程式は,分母・分子を$x$で割ることで同次形になりますね.
常微分方程式$y'(x)=\frac{3x+5y(x)}{x-y(x)}$を解け.
問題の常微分方程式は$y'(x)=\frac{3+5\frac{y(x)}{x}}{1-\frac{y(x)}{x}}$と変形できる.未知関数$u$を$u(x)=\frac{y(x)}{x}$で定めると,$xu(x)=y(x)$なので両辺を$x$で微分して
\begin{align*}u(x)+xu'(x)=y'(x)\end{align*}
が成り立つ.よって,常微分方程式は
\begin{align*}&u(x)+xu'(x)=\frac{3+5u(x)}{1-u(x)}
\\&\iff u'(x)=\frac{3+4u(x)+u(x)^2}{x(1-u(x))}
\\&\iff u'(x)=\frac{(u(x)+1)(u(x)+3)}{x(1-u(x))}\end{align*}
と変形できる.定数関数$u(x)\equiv-1,-3$はいずれも解で,他に定数関数解は存在しない.
また,定数関数でない解$u(x)$は(初期値問題の一意性より)値−1と値−3をとらないので,両辺を$\frac{(u(x)+1)(u(x)+3)}{1-u(x)}$で割って$x$で積分すると
\begin{align*}&\int\frac{1-u}{(u+1)(u+3)}\,du=\int\frac{1}{x}\,dx
\\&\iff\int\bra{\frac{1}{u+1}-\frac{2}{u+3}}\,du=\int\frac{1}{x}\,dx
\\&\iff\log{\frac{|u(x)+1|}{(u(x)+3)^2}}=\log|x|+C
\\&\iff\frac{u(x)+1}{(u(x)+3)^2}=\pm e^C x\end{align*}
と解ける.ただし,$C$は任意定数で,最後の等式は複号同順である.この解は定数関数解$u(x)\equiv-1$と併せて,任意定数$D$を用いて$\frac{u(x)+1}{(u(x)+3)^2}=Dx$と表せる.分母を払うと$u(x)$の2次方程式となるから,これを解いて
\begin{align*}u(x)=\frac{1-6Dx\pm\sqrt{1-8Dx}}{2Dx}\end{align*}
を得る.$u(x)=\frac{y(x)}{x}$より,解$y(x)$は
\begin{align*}y(x)=-3x,\quad
y(x)=\frac{1-6Dx\pm\sqrt{1-8Dx}}{2D}\end{align*}
である.

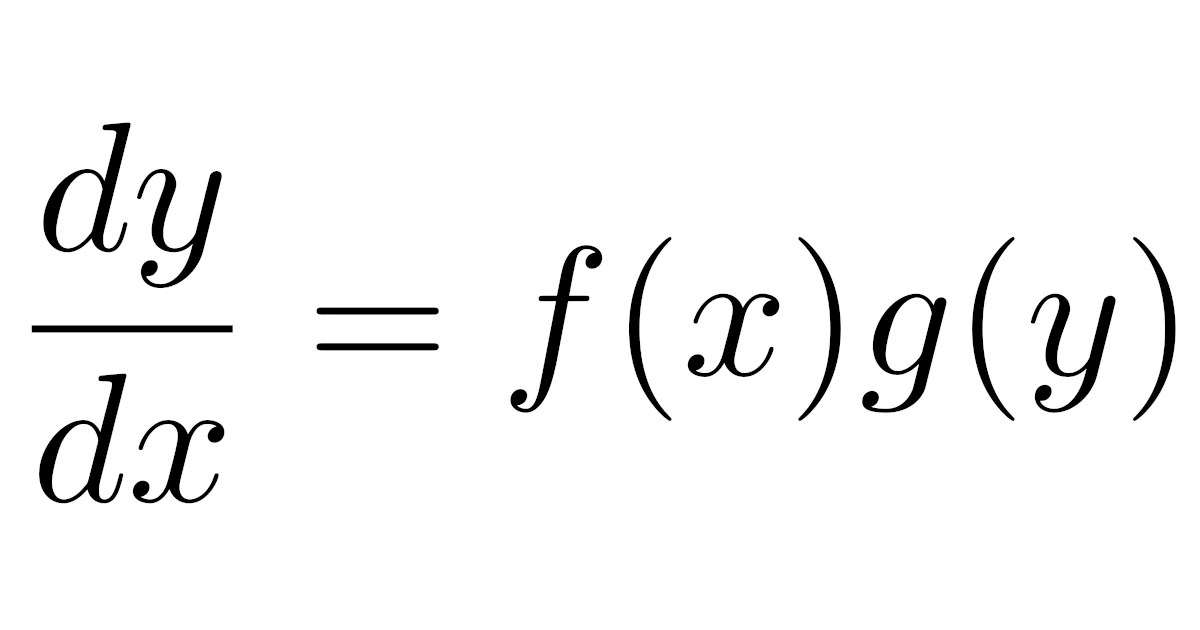
コメント