 東京大学|大学院入試
東京大学|大学院入試 2024大学院入試|東京大学 数理科学専攻|専門科目B
2024年度の京都大学 理学研究科 数理科学専攻の大学院入試問題の専門科目Bの解答例です.18題出題され,3題を選択して解答します.試験時間は4時間です.
 東京大学|大学院入試
東京大学|大学院入試 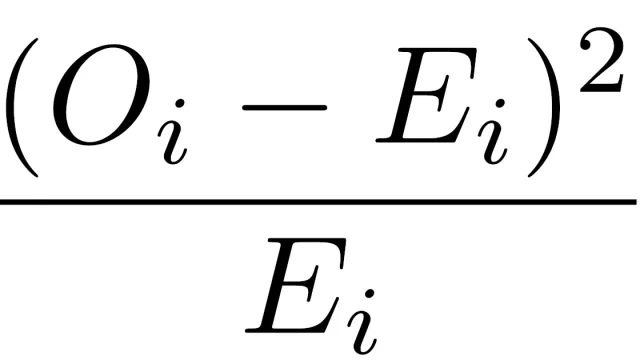 仮説検定
仮説検定 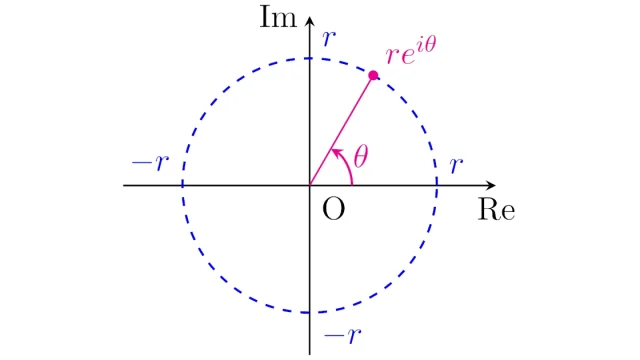 複素解析の基本
複素解析の基本 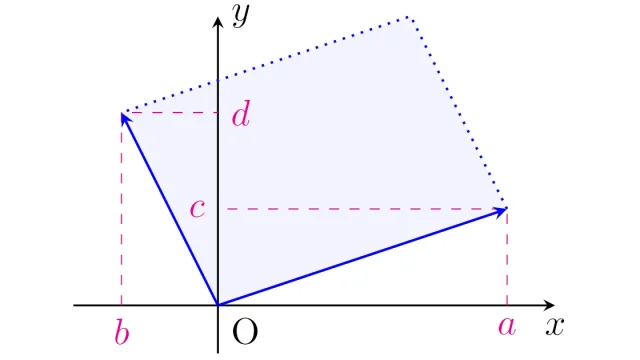 線形代数学
線形代数学 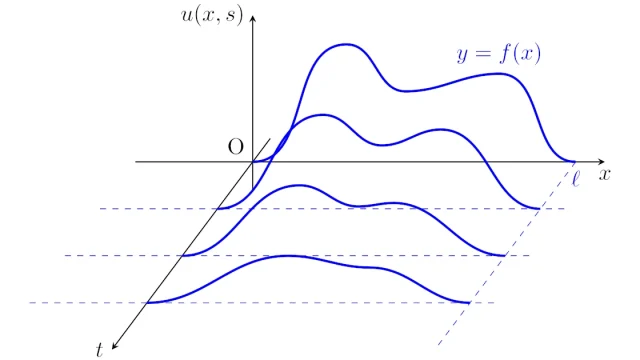 微分方程式
微分方程式 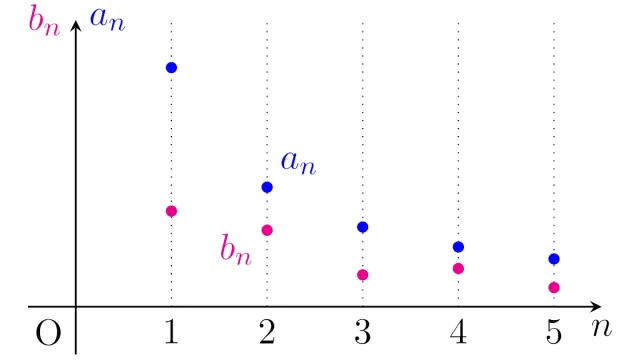 微分積分学の基本
微分積分学の基本 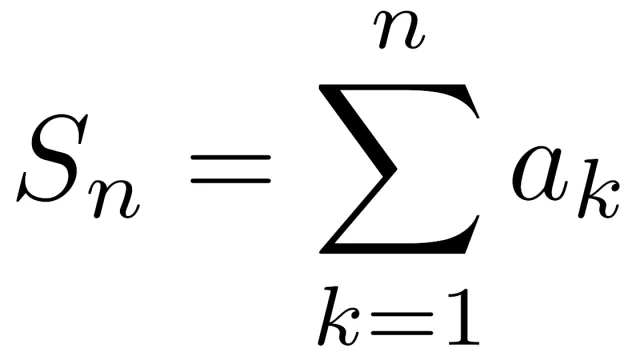 微分積分学の基本
微分積分学の基本 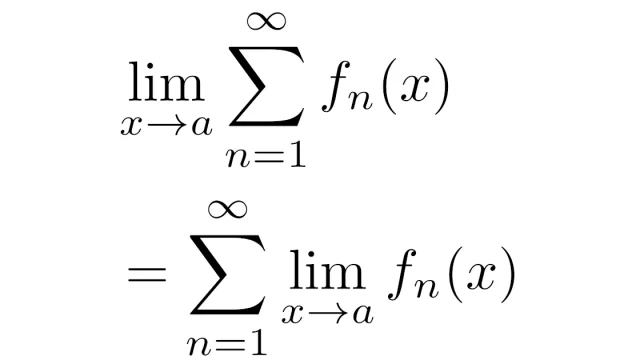 測度論
測度論 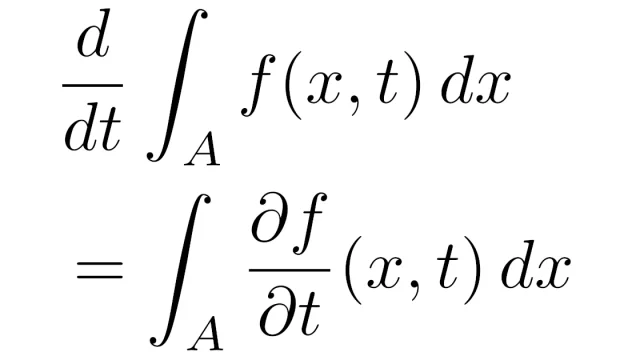 ルベーグ積分の基本
ルベーグ積分の基本 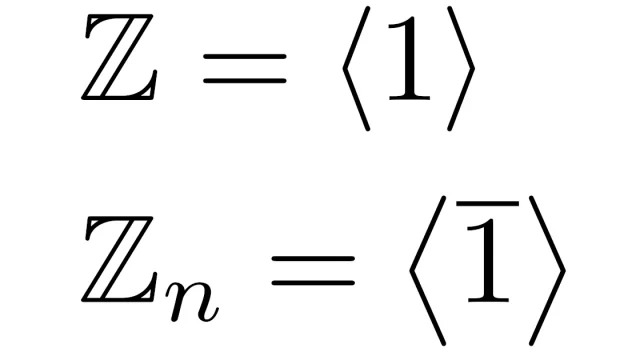 群論の基本
群論の基本