偏微分方程式において,
- 解が存在するか
- 解が存在するなら一意か
ということは当たり前でないことも多く,最先端の研究でも広く研究されています.
そこで「正当な」解について考察する前に,解を少し弱めた弱解の存在と一意性を議論することがよくあります.
この偏微分方程式の弱解の存在と一意性を示すために有用な定理としてラックス-ミルグラムの定理があります.
実はラックス-ミルグラムの定理は「ヒルベルト空間上の有界線形汎関数は内積で表せる」というリースの表現定理の拡張となっています.
この記事ではいくつかの予備知識を確認し,ラックス-ミルグラムの定理の主張を述べ証明をします.
準備
ラックス-ミルグラムの定理を理解するために必要な幾つかの概念を準備しておきます.
双線形形式
ラックス-ミルグラムの定理の主張の中に有界かつ強圧的な双線形形式が登場するので,まずはこの定義をしておきましょう.
実線形空間$V$に対して,写像$B:V\times V\to\R$が次のいずれも満たすとき,$B$を$V$上の双線形形式(bilinear form)または双線形写像(bilinear map)という.
- 任意の$u,v,w\in V$に対して,\begin{align*}&B(u+v,w)=B(u,w)+B(v,w),\\&B(u,v+w)=B(u,v)+B(u,w)\end{align*}
- 任意の$u,v\in V$と$k\in\R$に対して,\begin{align*}B(ku,v)=B(u,kv)=kB(u,v)\end{align*}
すなわち,線形空間の2元からスカラーを返す写像で,各変数について線形となっている写像のことを双線形形式というわけですね.
双線形形式を定義するだけなら$V$は線形空間でよいですが,有界性と強圧性は$V$がノルムが定まっていないと定義されないことに注意してください.
実ノルム空間$(V,\|\cdot\|)$上の双線形形式$B:V\times V\to\R$に対して,次のように定義する
- $B$が有界(bounded)であるとは,ある$C>0$が存在して,任意の$u,v\in V$に対して$|B(u,v)|\le C\|u\|\|v\|$が成り立つことをいう.
- $B$が強圧的(coercive)であるとは,ある$D>0$が存在して,任意の$u\in V$に対して$D\|u\|^2\le B(u,u)$が成り立つことをいう.
例えば,$V$が内積空間なら$V$の内積$\anb{\cdot,\cdot}$は有界で強圧的な双線形形式です.
- コーシー-シュワルツの不等式より,任意の$u,v\in V$に対して$|\anb{u,v}|\le\|u\|\|v\|$
- 内積とノルムの関係(ノルムの定義)より,任意の$u\in V$に対して$\|u\|^2=|\anb{u,u}|$
を満たすことから,上の定義で$C=D=1$と取れますね.
有界線形汎関数
ラックス-ミルグラムの定理の主張のなかに,有界な線形汎函数も登場するので,次はこれらを定義しましょう.
まずは線形汎函数の定義です.
実線形空間$V$に対して,写像$f:V\to\R$を$V$上の汎関数(functional)という.
さらに,$V$上の線形な汎関数を線形汎函数(linear functional)という.
すなわち,実線形空間$V$から実線形空間$\R$への線形写像を$V$上の線形汎関数というわけですね.
双線形形式と同じく,有界性は$V$がノルム空間の場合に定義されます.
実ノルム空間$(V,\|\cdot\|)$上の線形汎関数$f:V\to\R$を考える.ある$C>0$が存在して,任意の$u\in V$に対して\begin{align*}|f(u)|\le C\|u\|\end{align*}が成り立つとき,$f$は有界(bounded)であるという.
リースの定理
実線形空間$V$上の有界線形汎関数$f:V\to\R$全部の集合を$V^*$と表し,$V^*$に
- 和:$f,g\in V^*$の和$f+g$を$(f+g)(u)=f(u)+g(u)$
- スカラー倍:$f\in V^*$の$\alpha\in\R$倍$\alpha f$を$(\alpha f)(u)=\alpha f(u)$
を定めると,$V^*$は線形空間となるのでした.この空間$V^*$を$V$の双対空間(dual space)または共役空間(conjugate space)といいますね.
リース(Riesz)の表現定理または単にリースの定理は,Hilbert空間$H$の双対空間の任意の元が内積を用いて表せるという定理です.
[リースの表現定理]Hilbert空間$(H,\anb{\cdot,\cdot})$を考える.任意の有界線形汎関数$f$(すなわち$f\in H^{*}$)に対して,ある$u\in H$が一意に存在して,任意の$v\in H$に対して$f(v)=\anb{v,u}$が成り立つ.
リースの定理には$\|f\|_{V^*}=\|v\|_V$を含めることもよくあります.
ラックス-ミルグラムの定理とその証明
それではラックス-ミルグラム(Lax-Milgram)の定理の紹介と証明に移ります.
ラックス-ミルグラムの定理
[ラックス-ミルグラムの定理]実ヒルベルト空間$(H,\anb{\cdot,\cdot})$上の有界かつ強圧的な双線形形式$B:H\times H\to\R$を考える.任意の有界線形汎関数$f$(すなわち$f\in H^{*}$)に対して,ある$u\in H$が一意に存在して,任意の$v\in H$に対して$f(v)=B(u,v)$が成り立つ.
簡単に言えば,ラックス-ミルグラムの定理は「有界かつ強圧的な双線形形式$B$を用いて,有界線形汎関数$f$が一意に$f=B(u,\cdot)$と表せる」ということですね.
例えば内積は有界かつ強圧的な双線形形式だったので,ラックス-ミルグラムの定理で$B$を内積ととることができ,これはリースの定理になっていますね.
そのため,ラックス-ミルグラムの定理はこのリースの定理の拡張と呼べるわけですね.
ラックス-ミルグラムの定理の証明
$B$は有界かつ強圧的だから
- ある$C>0$が存在して,任意の$u,v\in V$に対して$|B(u,v)|\le C\|u\|\|v\|$
- ある$D>0$が存在して,任意の$u\in V$に対して$D\|u\|^2\le B(u,u)$
が成り立つ.
一意性の証明
まず存在すれば一意であることを示す.
$u,u’\in H$が任意の$v\in H$に対して$B(u,v)=f(v)$, $B(u’,v)=f(v)$を満たすとする.
このとき,$v=u-u’$とおいて,辺々引けば$B$の線形性より
\begin{align*}0=B(u-u’,v)=B(u-u’,u-u’)\le D\|u-u’\|\end{align*}
となるから$u=u’$を得る.
存在の証明
任意の$u\in H$に対して,$H$上の汎関数
\begin{align*}g:H\to\R; v\mapsto B(u,v)\end{align*}
は$B$が有界な双線形形式だから有界線形汎関数である.よって,リースの表現定理より$g=\anb{\cdot,w_g}_H$なる$w_g\in H$が一意に存在する.
いま$u\mapsto g\mapsto w_g$と定まったから,この$u\in H$から$w_g\in H$への作用素を$T$とする.このとき
\begin{align*}B(u,v)=g(v)=\anb{v,w_g}=\anb{v,Tu}=\anb{Tu,v}\end{align*}
が成り立つ.また,仮定より$f$は有界線形汎関数だから,リースの表現定理より,ある$w\in H$が存在して$f=\anb{\cdot,w}$が成り立つ.
ここで$T$の値域$R(T)$が$H$であれば,ある$u\in H$が存在して$Tu=w$を満たすから
\begin{align*}B(u,v)=\anb{Tu,v}=\anb{w,v}=\anb{v,w}=f(v)\end{align*}
が成り立つ.したがって,あとは$R(T)=H$を示せばよく,これを4ステップに分けて示す.
[ステップ1]$T$は$H$上の有界線形作用素であることを示す.
任意に$v\in V$をとる.$B$は双線形形式だから,任意の$u,u’\in H$と$\alpha\in\R$に対して
\begin{align*}\anb{T(\alpha u+u’),v}&=B(\alpha u+u’,v)=\alpha B(u,v)+B(u’,v)
\\&=\alpha \anb{Tu,v}+\anb{Tu’,v}=\anb{\alpha Tu+Tu’,v}\end{align*}
が成り立つ.第2成分の$v$は任意だったから,$T(\alpha u+u’)=\alpha Tu+Tu’$が成り立つ.
また,$B$は有界だから,任意の$u\in H$に対して
\begin{align*}\|Tu\|^2=\anb{Tu,Tu}=B(u,Tu)\le C\|u\|\|Tu\|\end{align*}
なので,これより$\|Tu\|\le C\|u\|$だから有界である.
[ステップ2]$T$は単射で逆作用素$T^{-1}$は有界作用素であることを示す.
$u\neq 0$なる$u\in H$に対して ,$B$が強圧的であることとCauchy-Schwarzの不等式から
\begin{align*}0<D\|u\|\le\frac{B(u,u)}{\|u\|}=\frac{\anb{Tu,u}}{\|u\|}\le\|Tu\|\end{align*}
なので,$\|Tu\|\neq0$だから$T$は単射である.
よって,逆作用素$T^{-1}$が存在し,$D\|u\|\le\|Tu\|$が成り立っているので$T^{-1}$は有界である.
[ステップ3]$T$の値域$R(T)$は閉であることを示す.
$R(T)$上の点列$\{u_n\}_{n\in\N}$が$u\in H$に収束するとする.このとき,任意の$n\in\N$に対して$u_n=Tu’_n$なる$u’_n\in H$が存在する.ステップ2で得られた不等式から
\begin{align*}D\|u’_n-u’_m\|\le\|T(u’_n-u’_m)\|=\|Tu’_n-Tu’_m\|=\|u_n-u_m\|\end{align*}
が成り立ち,$\{u_n\}$は収束列だからコーシー列なので$\{u’_n\}$もCauchy列である.
よって,$H$の完備性より極限$u’:=\lim\limits_{n\to\infty}u’_n$が存在するから,$u_n=Tu’_n$の両辺で$n\to\infty$をとって$u=Tu’\in R(T)$を得る.ただし,$T$は有界線形なので連続であることを用いた.
したがって,$R(T)$は閉である.
[ステップ4]$T$の値域$R(T)$が$H$であることを背理法により示す.
もし$R(T)\subsetneq H$と仮定すると,任意の$H\setminus R(T)$の元は$w_1+w_2$($w_1\in R(T)$, $w_2\in R(T)^{\perp}$)と表せて$w_2\neq0$である.一方,
\begin{align*}D\|w_2\|\le B(w_2,w_2)=\anb{Tw_2,w_2}=0\end{align*}
となって$w_2=0$だから,これは矛盾で$R(T)=H$を得る.
ステップ4では,一般にHilbert空間$H$は閉部分空間$M$によって$H=M\oplus M^{\perp}$と直交補空間を用いて分解できることを用いました.

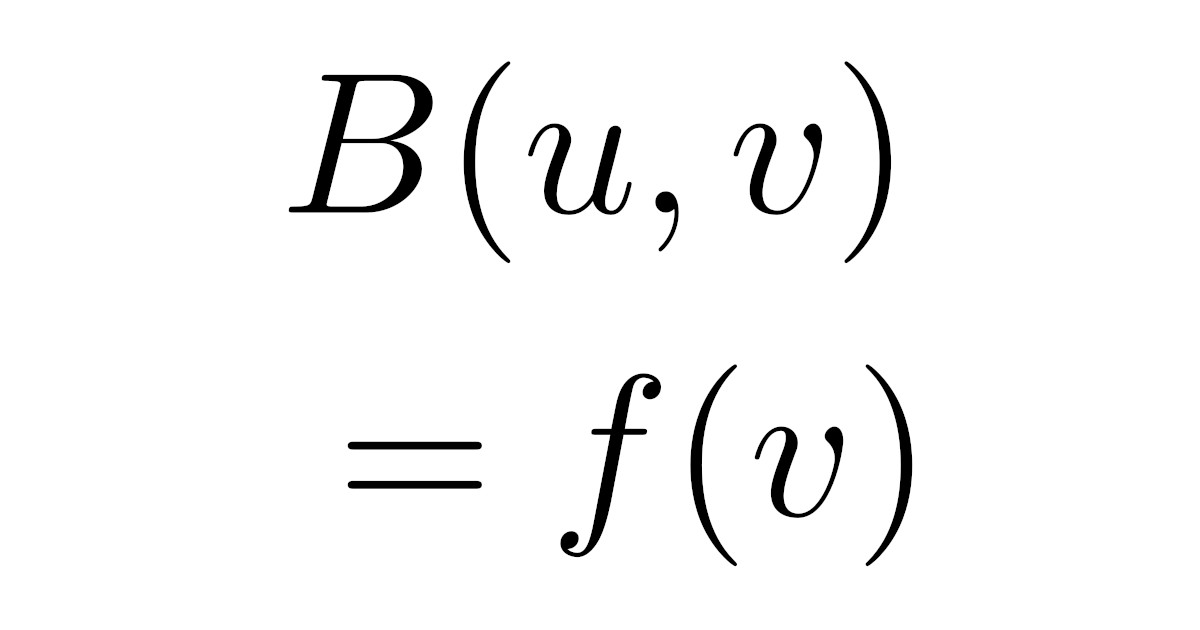
コメント