2次方程式$ax^2+bx+c=0$の解が
\begin{align*}x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\end{align*}
であることはよく知られており,これを2次方程式の解の公式といいますね.
そこで2次方程式の解の公式があるなら3次方程式の解の公式はどうなのか,つまり次の問題を考えることは自然なことでしょう.
3次方程式$ax^3+bx^2+cx+d=0$はいつでも係数$a,b,c,d$を用いて解けるのか?
ここでの「係数$a,b,c,d$を用いて解く」とは,正確には「係数$a,b,c,d$の有限回の四則演算と冪根をとる操作で解を表す」という意味です.
歴史的には2次方程式の解の公式は紀元前より知られていたものの,3次方程式の解の公式が発見されるには16世紀まで待たなくてはなりません.
この記事では
- 3次方程式の解の公式(カルダノの公式)の導出
- 3次方程式の解の公式の具体例
- 3次方程式の解の公式が広まった歴史的経緯
- 参考文献
を順に解説します.
3次方程式の解の公式(カルダノの公式)の導出
さっそく3次方程式$ax^3+bx^2+cx+d=0$の解の公式を導きましょう.ただし,以下では$a,b,c,d$は複素数とします.
導出は大雑把には
- 3次方程式を$X^3+pX+q=0$の形に変形する
- $X^3+y^3+z^3-3Xyz$の因数分解を用いる
の2ステップに分けられます.
ステップ1:方程式の変形
3次方程式$ax^3+bx^2+cx+d=0$は$x=X-\frac{b}{3a}$とおくことで
\begin{align*}X^3+pX+q=0\end{align*}
の形となる.
3次方程式としているので$a\neq0$ですから,$x=X-\frac{b}{3a}$の第2項で$a$で割っているのは問題ありませんね.
$x=X-\frac{b}{3a}$をもとの3次方程式$ax^3+bx^2+cx+d=0$に代入して
\begin{align*}&a\bra{X-\frac{b}{3a}}^3+b\bra{X-\frac{b}{3a}}^2+c\bra{X-\frac{b}{3a}}+d=0
\\\iff&a\bra{X^3-\frac{b}{a}X^2+\frac{b^2}{3a^2}X-\frac{b^3}{27a^3}}
\\&+b\bra{X^2-\frac{2b}{3a}X+\frac{b^2}{9a^2}}+c\bra{X-\frac{b}{3a}}+d=0
\\\iff&aX^3+\frac{-b^2+3ac}{3a}X+\frac{2b^3-9abc+27a^2d}{27a^2}=0
\\\iff&X^3+\frac{-b^2+3ac}{3a^2}X+\frac{2b^3-9abc+27a^2d}{27a^3}=0\end{align*}
となります.よって,
\begin{align*}p=\frac{-b^2+3ac}{3a^2},\quad
q=\frac{2b^3-9abc+27a^2d}{27a^3}\end{align*}
とすれば,3次方程式$ax^3+bx^2+cx+d=0$は$X^3+pX+q=0$となりますね.
ステップ2:3次式の因数分解公式と解
3次方程式$X^3+pX+q=0$は因数分解
\begin{align*}&X^3+y^3+z^3-3Xyz\\&=(X+y+z)(X+\omega y+\omega^2z)(X+\omega^2 y+\omega z)\end{align*}
を用いることで解ける.ただし,$\omega$は1の原始3乗根の1つである.
1の原始3乗根とは「3乗して初めて1になる複素数」のことで,$x^3=1$の1でない2つの虚数解はどちらも1の原始3乗根です.そのため,$\omega$は
\begin{align*}1-\omega^3=0
\iff& (1-\omega)(1+\omega+\omega^2)=0
\\\iff& 1+\omega+\omega^2=0\end{align*}
を満たしますね.
この因数分解はこのあとの補足で証明しています.
因数分解
\begin{align*}&X^3+y^3+z^3-3Xyz
\\&=(X+y+z)(X+\omega y+\omega^2z)(X+\omega^2 y+\omega z)\end{align*}
が成り立つので,3次方程式$X^3+pX+q=0$の左辺と比較して
\begin{align*}\begin{cases}-3yz=p\\ y^3+z^3=q\end{cases}\end{align*}
を満たす$y$, $z$を$p$, $q$で表すことができれば,方程式$X^3+pX+q=0$の解
\begin{align*}X=-y-z,-y\omega-z\omega^2,-y\omega^2-z\omega\end{align*}
を$p$, $q$で表すことができますね.
さて,先ほどの連立方程式より
\begin{align*}\begin{cases}y^3z^3=-\frac{p^3}{27}\\ y^3+z^3=q\end{cases}\end{align*}
となるので,2次方程式の解と係数の関係より$t$の2次方程式
\begin{align*}t^2-qt-\frac{p^3}{27}=0\end{align*}
は$y^3$, $z^3$を解にもちます.一方,2次方程式の解の公式より,この方程式の解は
\begin{align*}t=&\frac{q\pm\sqrt{q^2+\frac{4p^3}{27}}}{2}
\\=&\frac{3\sqrt{3}q\pm\sqrt{27q^2+4p^3}}{6\sqrt{3}}\end{align*}
となります.$y$, $z$は対称なので
\begin{align*}&y=\sqrt[3]{\frac{3\sqrt{3}q+\sqrt{27q^2+4p^3}}{6\sqrt{3}}},
\\&z=\sqrt[3]{\frac{3\sqrt{3}q-\sqrt{27q^2+4p^3}}{6\sqrt{3}}}\end{align*}
として良く,これで3次方程式$X^3+pX+q=0$が解けました.
カルダノの公式(3次方程式の解の公式)
以上より,3次方程式の解の公式は以下のようになります.
[カルダノの公式(3次方程式の解の公式)]複素数$a,b,c,d$に対し,3次方程式$ax^3+bx^2+cx+d=0$の解は
\begin{align*}
x=&-\frac{b}{3a}-\sqrt[3]{\frac{3\sqrt{3}q+\sqrt{27q^2+4p^3}}{6\sqrt{3}}}-\sqrt[3]{\frac{3\sqrt{3}q-\sqrt{27q^2+4p^3}}{6\sqrt{3}}},
\\&-\frac{b}{3a}-\sqrt[3]{\frac{3\sqrt{3}q+\sqrt{27q^2+4p^3}}{6\sqrt{3}}}\omega-\sqrt[3]{\frac{3\sqrt{3}q-\sqrt{27q^2+4p^3}}{6\sqrt{3}}}\omega^2,
\\&-\frac{b}{3a}-\sqrt[3]{\frac{3\sqrt{3}q+\sqrt{27q^2+4p^3}}{6\sqrt{3}}}\omega^2-\sqrt[3]{\frac{3\sqrt{3}q-\sqrt{27q^2+4p^3}}{6\sqrt{3}}}\omega
\end{align*}
である.ただし,
- $p=\dfrac{-b^2+3ac}{3a^2}$
- $q=\dfrac{2b^3-9abc+27a^2d}{27a^3}$
- $\omega$は$1$の原始$3$乗根
である.
$p$, $q$を実際に代入すると,解は$a,b,c,d$の有限回の四則演算と冪根を用いて解けることが分かりますね.
補足($X^3+y^3+z^3-3Xyz$の因数分解)
念のため,途中で用いた因数分解を証明しておきましょう.
因数分解
\begin{align*}&X^3+y^3+z^3-3Xyz\\&=(X+y+z)(X+\omega y+\omega^2z)(X+\omega^2 y+\omega z)\end{align*}
が成り立つ.
因数分解
\begin{align*}X^3+y^3+z^3-3Xyz=(X+y+z)(X^2+y^2+z^2-Xy-yz-zX)\end{align*}
が成り立ちます.さらに,1の原始3乗根の性質$\omega^3=1$, $\omega^2+\omega=-1$より
\begin{align*}&(X+\omega y+\omega^2z)(X+\omega^2 y+\omega z)
\\&=X^2+\omega^3y^2+\omega^3z^2+(\omega+\omega^2)Xy+(\omega+\omega^2)yz+(\omega+\omega^2)zX
\\&=X^2+y^2+z^2-Xy-yz-zX\end{align*}
なので,示されました.
3次方程式の解の公式の具体例
解の公式と言ってはいるものの,上の公式に直接代入して解を求めるのは大変で現実的ではありません.
解の公式の導出の手順を当てはめて解くのが良いでしょう.
$x$の方程式$x^3-3x^2-3x-4=0$を解け.
単純に$(x-4)(x^2+x+1)=0$と左辺が因数分解できることから,解は
\begin{align*}x=4,\frac{-1\pm\sqrt{3}i}{2}\end{align*}
と得られますが,カルダノの公式を使っても同じ解が得られることを確かめましょう.
$x=X+1$とおくと,方程式$x^3-3x^2-3x-4=0$は
\begin{align*}&(X+1)^3-3(X+1)^2-3(X+1)-4=0
\\\iff&(X^3+3x^2+3x+1)-3(X^2+2X+1)-3(X+1)-4=0
\\\iff&X^3-6X-9=0\end{align*}
となる.因数分解
\begin{align*}&X^3-3yzX+(y^3+z^3)
\\=&(X+y+z)(X+\omega y+\omega^2z)(X+\omega^2 y+\omega z)\end{align*}
と比較して,
\begin{align*}\begin{cases}-3yz=-6\\ y^3+z^3=-9\end{cases}\end{align*}
なる$y$, $z$を見つけることができれば,解は
\begin{align*}X=-y-z,-\omega y-\omega^2z,-\omega^2 y-\omega z\end{align*}
となる.$y^3z^3=8$と$y^3+z^3=-9$だから,2次方程式の解と係数の関係より,$t$の2次方程式
\begin{align*}t^2+9t+8=0\end{align*}
は解$y^3$, $z^3$をもつ.この$t$の2次方程式は左辺を因数分解して
\begin{align*}(t+1)(t+8)=0\iff
t=-1,-8\end{align*}
と解けるから,$y$, $z$の対称性より$(y^3,z^3)=(-1,-8)$としてよく,さらに$yz=2$に注意して$(y,z)=(-1,-2)$としてよい.
以上より,求める解は
\begin{align*}x&=X+1
\\&=-(-1)-(-2)+1,-(-1)\omega-(-2)\omega^2+1,-(-1)\omega^2-(-2)\omega+1
\\&=4,\omega+2\omega^2+1,\omega^2+2\omega+1
\\&=4,\omega^2,\omega
\\&=4,\frac{-1\pm\sqrt{3}i}{2}\end{align*}
である.
確かに因数分解して得られた解と一致しましたね.
$(y,z)=(-2,-1)$や$(y,z)=(-\omega,-2\omega^2)$などとしても,最終的に
\begin{align*}-y-z,\quad
-y\omega-z\omega^2,\quad
-y\omega^2-z\omega\end{align*}
たちがうまく入れ替わって,全体として同じ解が得られます.
3次方程式の解の公式が広まった歴史的経緯
おまけとして最後に3次方程式の解の公式が知られるようになった経緯を説明しておきます.
ジェロラモ・カルダノ
かつてイタリアでは数学の問題を出し合って勝負する公開討論会が行われていた時代がありました.
公開討論会では3次方程式は難問とされており,多くの人によって3次方程式の解の公式の導出が試みられました.
そんな中,16世紀の半ばにジェロラモ・カルダノ(Gerolamo Cardano)により著書「アルス・マグナ(Ars Magna)」が執筆され,その中で3次方程式の解の公式が示されました.
アルス・マグナの意味は「偉大な術」であり,副題は「代数学の諸法則」でした.
このようにカルダノによって3次方程式の解の公式は世の中の知るところとなったわけですが,この3次方程式の解の公式について
- シピオーネ・デル・フェロ(Scipione del Ferro)
- ニコロ・フォンタナ(Niccolò Fontana)
が重要な人物なので紹介します.
デル・フェロとフォンタナ
15世紀後半の数学者であるデル・フェロが3次方程式の解の公式を最初に導出したとされています.
デル・フェロは自身の研究をあまり公表しなかったため,彼の導出した3次方程式の解の公式が日の目を見ることはありませんでした.
しかし,デル・フェロは自身の研究成果を弟子に託しており,弟子の一人であるアントニオ・マリア・デル・フィオール (Antonio Maria del Fiore)はこの結果をもとに討論会で勝ち続けていたそうです.
そんな折,デル・フェロと同じく数学者のフォンタナは3次方程式の解の公式があるとの噂を聞き,フォンタナは独自に3次方程式の解の公式を導出しました.
実はデル・フェロ(フィオール)の公式は全ての3次方程式に対して適用することができなかった一方で,フォンタナの公式は全ての3時方程式に対して解を求めることができるものでした.
そのため,フォンタナは討論会でフィオールが解けないパターンの問題を出題することで勝利し,3次方程式の解の公式を導いたらしいとフォンタナの名前が広まることとなりました.
カルダノとフォンタナ
後にアルス・マグナを発刊するカルダノもフォンタナの噂を聞きつけ,フォンタナのもとを訪れます.
カルダノは「公式を発表しない」という約束のもとに,フォンタナから3次方程式の解の公式を聞き出すことに成功します.
しかし,しばらくしてカルダノは上で紹介したデル・フェロの公式を導出した原稿を発見し,フォンタナの前にデル・フェロが公式を得ていたことを知ります.
そこでカルダノは「公式はフォンタナによる発見ではなくデル・フェロによる発見であり約束を守る必要はない」と考え,アルス・マグナの中でデル・フェロの解法と名付けて3次方程式の解の公式を紹介しました.
同時にカルダノは最初に自身はフォンタナから教わったことも記していますが,約束を反故にされたフォンタナは当然激怒しました.
その後,フォンタナはカルダノに勝負を申し込みましたが,カルダノは受けなかったと言われています.
以上のように,現在ではこの記事で説明する3次方程式の解の公式はカルダノの公式と呼ばれていますが,カルダノによって発見されたわけではなく,デル・フェロとフォンタナによって別々に発見されたわけですね.
参考文献
以下は参考文献です.
数学の真理をつかんだ25人の天才たち
[イアン・スチュアート 著/水谷淳 訳/ダイヤモンド社]
アルキメデス,オイラー,ガウス,ガロア,ラマヌジャンといった数学上の25人の偉人が,時系列順にざっくりとまとめられた伝記です.
カルダノもこの本の中で紹介されています.
しかし,上述したようにカルダノ自身が重要な発見をしたわけではないので,カルダノがなぜ「数学の真理をつかんだ天才」とされているのか,個人的には正直なところ疑問ではあるのですが……
とはいえ,ほとんどが数学界を大きく発展させるような発見をした人物が数多く取り上げられています.
「こんな偉大な人物が実はそんな人間だったのか」と意外な一面を知ることができる一冊です.

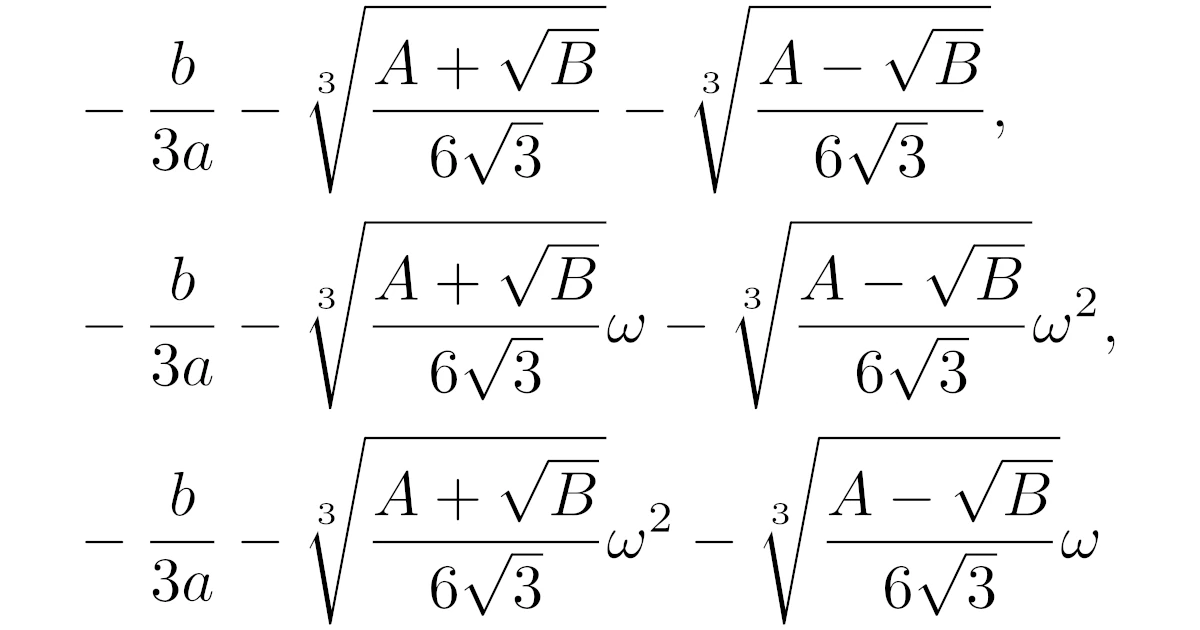

コメント