 偏微分方程式
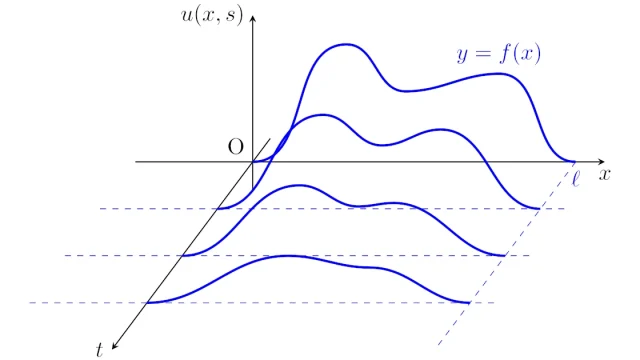
偏微分方程式 1次元線形熱方程式の変数分離解をフーリエ級数を用いて導出
線形熱方程式の初期値・境界値問題では,解がフーリエ級数展開を用いて表せる場合が多くあります.この記事では,形式的に解の形を導出したのち,その形式的な解が厳密解であることを証明します.
 偏微分方程式
偏微分方程式  偏微分方程式
偏微分方程式  偏微分方程式
偏微分方程式  偏微分方程式
偏微分方程式  偏微分方程式
偏微分方程式  偏微分方程式
偏微分方程式  偏微分方程式
偏微分方程式