3次元ユークリッド空間$\R^3$上の滑らかな曲線$C:\m{r}=\m{r}(t)$に対して
- 「進む向き」を表す単位接ベクトル$\m{v}_1$
- 「曲がる向き」を表す主法線ベクトル$\m{v}_2$
- 「ねじれる向き」を表す従法線ベクトル$\m{v}_3$
を考えることができます.
これらのベクトルは正規直交基底をなしており,${\m{v}_1}’$, ${\m{v}_2}’$, ${\m{v}_3}’$を$\m{v}_1$, $\m{v}_2$, $\m{v}_3$の線形結合で表す公式をフルネ-セレ(Frenet-Serret)の公式(フレネ-セレの公式)といいます.
この記事では
- 空間曲線の基礎知識
- フルネ-セレの公式と曲率・捩率
- フルネ-セレの公式の証明
を順に解説します.
空間曲線の基礎知識
以下,$\alpha<\beta$とします.
基本的に閉区間$[\alpha,\beta]$上で定義された連続関数を考えますが,導関数が関わる場合は開区間$(\alpha,\beta)$上で考えます.
空間曲線の考え方と定義
曲線とは直観的には「ちぎれていない曲線」のことですが,もう少しきちんと定義しましょう.
時刻$t=\alpha$から時刻$t=\beta$まで連続的に点が動く状況を考え,時刻$t$での点の位置を$\m{r}(t)$と表すことにすると,この$\m{r}$は閉区間$[\alpha,\beta]$で定義された連続写像と考えることができますね.
このことを踏まえて,次のように空間曲線を定義します.
1変数ベクトル値関数$\m{r}:[\alpha,\beta]\to\R^3$を空間曲線という.
位相空間をあまり知らない方はあまり気にしなくても良いですが,この定義で$[\alpha,\beta]$は1次元ユークリッド空間$\R$の部分位相空間,$\R^3$は3次元ユークリッド空間です.
空間曲線の導関数
空間曲線$\m{r}:(\alpha,\beta)\to\R^3$の各成分が微分可能であるとき,$\m{r}$は微分可能であるといいます.
空間曲線$\m{r}:[\alpha,\beta]\to\R^3$を
\begin{align*}\m{r}=\bmat{r_1\\r_2\\r_3},\quad
r_i:[\alpha,\beta]\to\R\quad(i=1,2,3)\end{align*}
と表すとき,$\m{r}$が(開区間$(\alpha,\beta)$上)微分可能であるとは,$r_1,r_2,r_3$がいずれも(開区間$(\alpha,\beta)$上)微分可能であることをいう.また,このとき$\m{r}$の導関数$\m{r}’$を
\begin{align*}\m{r}’=\bmat{r’_1\\r’_2\\r’_3}\end{align*}
で定める.
空間曲線の内積の微分公式
[内積の微分公式]微分可能な空間曲線$\m{r},\m{s}:[\alpha,\beta]\to\R^3$を考える.任意の$t\in(\alpha,\beta)$に対して,
\begin{align*}&\frac{d\anb{\m{r},\m{s}}}{dt}(t)=\anb{\m{r}'(t),\m{s}(t)}+\anb{\m{r}(t),\m{s}'(t)}\end{align*}
が成り立つ.ただし,$\anb{\cdot,\cdot}$は通常の内積(標準内積)である.
通常の関数の積の微分公式$(fg)’=f’g+fg’$と同様の形をしているので覚えやすいですね.
$\m{r}=\bmat{r_1\\r_2\\r_3}$, $\m{s}=\bmat{s_1\\s_2\\s_3}$とすると,内積の定義より
\begin{align*}\anb{\m{r},\m{s}}=r_1s_1+r_2s_2+r_3s_3=\sum_{i=1}^{3}r_is_i\end{align*}
なので,積の微分公式を用いて
\begin{align*}\od{\anb{\m{r},\m{s}}}{t}
&=\sum_{i=1}^{3}\bra{r’_is_i+r_is’_i}
\\&=\sum_{i=1}^{3}r’_is_i+\sum_{i=1}^{3}r_is’_i
\\&=\anb{\m{r}’,\m{s}}+\anb{\m{r},\m{s}’}\end{align*}
が成り立つ.
空間曲線の外積の微分公式
[外積の微分公式]微分可能な空間曲線$\m{r},\m{s}:[\alpha,\beta]\to\R^3$を考える.任意の$t\in(\alpha,\beta)$に対して,
\begin{align*}\frac{d(\m{r}\times \m{s})}{dt}(t)=\m{r}'(t)\times \m{s}(t)+\m{r}(t)\times \m{s}'(t)\end{align*}
が成り立つ.ただし,$\times$は$\R^3$上の外積である.
内積のときと同じく,外積でも通常の関数の積の微分公式$(fg)’=f’g+fg’$と同様の形をしているので覚えやすいですね.
$\m{r}=\bmat{r_1\\r_2\\r_3}$, $\m{s}=\bmat{s_1\\s_2\\s_3}$とすると,外積の定義より
\begin{align*}\m{r}\times \m{s}=\bmat{r_2s_3-r_3s_2\\r_3s_1-r_1s_3\\r_1s_2-r_2s_1}\end{align*}
なので,各成分で積の微分公式を用いて
\begin{align*}\od{(\m{r}\times \m{s})}{t}
&=\bmat{(r’_2s_3+r_2s’_3)-(r’_3s_2+r_3s’_2)\\(r’_3s_1+r_3s’_1)-(r’_1s_3+r_1s’_3)\\(r’_1s_2+r_1s’_2)-(r’_2s_1+r_2s’_1)}
\\&=\bmat{r’_2s_3-r’_3s_2\\r’_3s_1-r’_1s_3\\r’_1s_2-r’_2s_1}+\bmat{r_2s’_3-r_3s’_2\\r_3s’_1-r_1s’_3\\r_1s’_2-r_2s’_1}
\\&=\m{r}’\times \m{s}+\m{r}\times \m{s}’\end{align*}
が従う.
補題(ノルムが一定のベクトル)
次の補題はベクトル解析・曲線曲面論ではよく用いられるので,ここで準備しておきます.
微分可能な空間曲線$\m{r}:[\alpha,\beta]\to\R^3$のノルム$\|\m{r}\|$が一定なら,任意の$t\in(\alpha,\beta)$に対して
\begin{align*}\anb{\m{r}(t),\m{r}'(t)}=0\end{align*}
が成り立つ.
$\|\m{r}\|$が一定なら,内積の微分公式と実内積の対称性より
\begin{align*}0&\equiv(\|\m{r}\|^2)’=\anb{\m{r},\m{r}}’
\\&=\anb{\m{r}’,\m{r}}+\anb{\m{r},\m{r}’}=2\anb{\m{r},\m{r}’}\end{align*}
が分かる.よって,両辺を2で割って$0\equiv\anb{\m{r},\m{r}’}$が従う.
フルネ-セレの公式と曲率・捩率
以下,空間曲線$\m{r}:[\alpha,\beta]\to\R^3$は
- $\m{r}$は$C^\infty$級($\m{r}$は何回でも微分可能)
- $\m{r}’\neq\m{0}$($\m{r}$が動く速さは0にならない)
- $\m{r}^{\prime\prime}\times \m{r}’\neq\m{0}$(曲線の軌跡は曲がっている)
を満たすとします.
単位接ベクトル$\m{v}_1$・主法線ベクトル$\m{v}_2$・従法線ベクトル$\m{v}_3$の定義
空間曲線$C:\m{r}=\m{r}(t)$に対し,
- 単位接ベクトル$\m{v}_1$:曲線$C$の「進む向き」
- 主法線ベクトル$\m{v}_2$:曲線$C$の「曲がる向き」
- 従法線ベクトル$\m{v}_3$:曲線$C$の「ねじれる向き」
を次で定義します.
空間曲線$C:\m{r}=\m{r}(t)$に対し,$\m{v}_1,\m{v}_2,\m{v}_3:(\alpha,\beta)\to\R^3$を
\begin{align*}\m{v}_1:=\frac{\m{r}’}{\|\m{r}’\|},\quad
\m{v}_2:=\frac{{\m{v}_1}’}{\|{\m{v}_1}’\|},\quad
\m{v}_3:=\m{v}_1\times \m{v}_2\end{align*}
で定義し,$\m{v}_1$を$C$の単位接ベクトル,$\m{v}_2$を$C$の主法線ベクトル,$\m{v}_3$を$C$の従法線ベクトルという.
$\m{v}_1$, $\m{v}_2$, $\m{v}_3$の正規直交性
これらのベクトル$\m{v}_1,\m{v}_2,\m{v}_3$については,次を当たり前にしておきましょう.
空間曲線$C:\m{r}=\m{r}(t)$の単位接ベクトル$\m{v}_1$,主法線ベクトル$\m{v}_2$,従法線ベクトル$\m{v}_3$は$\R^3$の正規直交基底をなす.
$\m{v}_1$, $\m{v}_2$の定義より,
\begin{align*}&\|\m{v}_1\|=\nor{\frac{\m{r}’}{\|\m{r}’\|}}=\frac{1}{\|\m{r}’\|}\|\m{r}’\|=1
\\&\|\m{v}_2\|=\nor{\frac{\m{v}’_1}{\|\m{v}’_1\|}}=\frac{1}{\|\m{v}’_1\|}\|\m{v}’_1\|=1\end{align*}
である.また,$\|\m{v}_1\|=1$だから,補題より
\begin{align*}\anb{\m{v}_1,\m{v}_2}=\anb{\m{v}_1,\frac{\m{v}’_1}{\|\m{v}’_1\|}}=\frac{1}{\|\m{v}’_1\|}\anb{\m{v}_1,\m{v}’_1}=0\end{align*}
である.さらに,外積の性質より$\m{v}_3=\m{v}_1\times \m{v}_2$は$\m{v}_1$, $\m{v}_2$と直交し,
\begin{align*}\|\m{v}_3\|=\abs{\|\m{v}_1\|\|\m{v}_2\|\sin{\bra{\pm\frac{\pi}{2}}}}=1\end{align*}
である.
フルネ-セレの公式
単位接ベクトル$\m{v}_1$,主法線ベクトル$\m{v}_2$,従法線ベクトル$\m{v}_3$が$\R^3$の(正規直交)基底をなすことから,これら3本のベクトル値関数の導関数$\m{v}’_1$, $\m{v}’_2$, $\m{v}’_3$を$\m{v}_1$, $\m{v}_2$, $\m{v}_3$の線形結合で一意に表すことができます.
この公式は
- 1847年にジャン・フレデリック・フルネ(Jean Frédéric Frenet)
- 1851年にジョセフ・アルフレッド・セレ(Joseph Alfred Serret)
によって独立に発見されましたのでフルネ-セレの公式といいます.
[フルネ-セレの公式]空間曲線$C:\m{r}=\m{r}(t)$は$\|\m{r}'(t)\|\equiv1$を満たすとする.このとき,ある非負値関数$\kappa:(\alpha,\beta)\to\R_{\ge0}$と実数値関数$\tau:(\alpha,\beta)\to\R$が存在して,任意の$t\in(\alpha,\beta)$に対して
\begin{align*}\begin{cases}\m{v}’_1(t)=\kappa(t)\m{v}_2(t)\\\m{v}’_2(t)=-\kappa(t)\m{v}_1(t)+\tau(t)\m{v}_3(t)\\\m{v}’_3(t)=-\tau(t)\m{v}_2(t)\end{cases}\end{align*}
が成り立つ.
$\|\m{r}'(t)\|\equiv1$を満たすとき,曲線上を点が進む速さが1ということなので,パラメータ$t$は弧長パラメータであるといいます.
フルネ-セレの公式は
\begin{align*}[\m{v}’_1(t),\m{v}’_2(t),\m{v}’_3(t)]=[\m{v}_1(t),\m{v}_2(t),\m{v}_3(t)]\bmat{0&\kappa(t)&0\\-\kappa(t)&0&\tau(t)\\0&-\tau(t)&0}\end{align*}
と表すこともできますね.
曲率・捩率の定義
上のフルネ-セレの公式の
- 非負値関数$\kappa:(\alpha,\beta)\to[0,\infty)$を空間曲線$C:\m{r}=\m{r}(t)$の曲率
- 実数値関数$\tau:(\alpha,\beta)\to\R$を空間曲線$C:\m{r}=\m{r}(t)$の捩率
という.
第1式の両辺でノルムをとれば
\begin{align*}\|\m{v}’_1\|=|\kappa|\|\m{v}_2\|=\kappa\end{align*}
となるので,曲率は単位接ベクトルの導関数$\m{v}’_1$のノルムとして定義することもできます.
フルネ-セレの公式の証明
それでは,フルネ-セレの公式を証明しましょう.
[フルネ-セレの公式(再掲)]空間曲線$C:\m{r}=\m{r}(t)$は$\|\m{r}'(t)\|\equiv1$を満たすとする.このとき,ある非負値関数$\kappa:(\alpha,\beta)\to\R_{\ge0}$と実数値関数$\tau:(\alpha,\beta)\to\R$が存在して,任意の$t\in(\alpha,\beta)$に対して
\begin{align*}\begin{cases}\m{v}’_1(t)=\kappa(t)\m{v}_2(t)\\\m{v}’_2(t)=-\kappa(t)\m{v}_1(t)+\tau(t)\m{v}_3(t)\\\m{v}’_3(t)=-\tau(t)\m{v}_2(t)\end{cases}\end{align*}
が成り立つ.
任意の$t\in(\alpha,\beta)$に対して$\m{v}_1(t)$, $\m{v}_2(t)$, $\m{v}_3(t)$は$\R^3$の基底をなすことに注意する.
第1式$\m{v}’_1=\kappa\m{v}_2$の証明
$\m{v}_2$の定義の両辺に$\|\m{v}’_1\|$をかけて
\begin{align*}\m{v}_2=\frac{\m{v}’_1}{\|\m{v}’_1\|}\iff \m{v}’_1=\|\m{v}’_1\|\m{v}_2\end{align*}
が成り立つので,$\kappa=\|\m{v}’_1\|$とおけば$\kappa$は非負値で第1式が成り立つ.
第3式$\m{v}’_3=-\tau\m{v}_2$の証明
$\m{v}_1$, $\m{v}_2$, $\m{v}_3$は$\R^3$の基底をなすから,
\begin{align*}\m{v}’_3=a_{1}\m{v}_1+a_{2}\m{v}_2+a_{3}\m{v}_3\end{align*}
で$a_{i}:(\alpha,\beta)\to\R$($i=1,2,3$)を定めることができる.$a_{1}=a_{3}\equiv0$を示せばよい.
$\|\m{v}_3\|\equiv1$だから,補題より$\anb{\m{v}_3,\m{v}’_3}\equiv0$が成り立つので
\begin{align*}0\equiv\anb{\m{v}_3,a_{1}\m{v}_1+a_{2}\m{v}_2+a_{3}\m{v}_3}=a_{3}\end{align*}
が成り立つ.また,内積の微分公式と,上で示した第1式を併せて
\begin{align*}a_{1}&=\anb{a_{1}\m{v}_1+a_{2}\m{v}_2,\m{v}_1}=\anb{\m{v}’_3,\m{v}_1}
\\&=\anb{\m{v}_3,\m{v}_1}’-\anb{\m{v}_3,\m{v}’_1}
\\&=0′-\anb{\m{v}_3,\kappa\m{v}_2}=-\kappa\anb{\m{v}_3,\m{v}_2}=0\end{align*}
が成り立つ.よって,$\tau=-a_2$とおけば第3式が成り立つ.
第2式$\m{v}’_2=-\kappa\m{v}_1+\tau\m{v}_3$の証明
$\m{v}_1$, $\m{v}_2$, $\m{v}_3$は$\R^3$の基底をなすから,
\begin{align*}\m{v}’_2=b_{1}\m{v}_1+b_{2}\m{v}_2+b_{3}\m{v}_3\end{align*}
で$b_{i}:(\alpha,\beta)\to\R$($i=1,2,3$)を定めることができる.$b_{2}\equiv0$, $b_{1}=-\kappa$, $b_{3}=\tau$を示せばよい.
$\|\m{v}_2\|=1$だから,補題より$\anb{\m{v}_2,\m{v}’_2}\equiv0$が成り立つので
\begin{align*}0\equiv\anb{\m{v}_2,b_{1}\m{v}_1+b_{2}\m{v}_2+b_{3}\m{v}_3}=b_{2}\end{align*}
が成り立つ.また,内積の微分公式と,上で示した第1式を併せて
\begin{align*}\kappa&=\kappa\anb{\m{v}_2,\m{v}_2}=\anb{\m{v}_2,\kappa\m{v}_2}=\anb{\m{v}_2,\m{v}’_1}
\\&=\anb{\m{v}_2,\m{v}_1}’-\anb{\m{v}’_2,\m{v}_1}
\\&=0′-\anb{b_{1}\m{v}_1+b_{3}\m{v}_3,\m{v}_1}=-b_{1}\end{align*}
だから$b_{1}=-\kappa$が成り立つ.さらに,内積の微分公式と,上で示した第3式を併せて
\begin{align*}\tau&=\tau\anb{\m{v}_2,\m{v}_2}=\anb{\m{v}_2,\tau\m{v}_2}=-\anb{\m{v}_2,\m{v}’_3}
\\&=-\{\anb{\m{v}_2,\m{v}_3}’-\anb{\m{v}’_2,\m{v}_3}\}
\\&=0′-\anb{-\kappa\m{v}_1+b_{3}\m{v}_3,\m{v}_3}=b_{3}\end{align*}
だから$b_{3}=\tau$が成り立つ.よって,第2式が成り立つ.

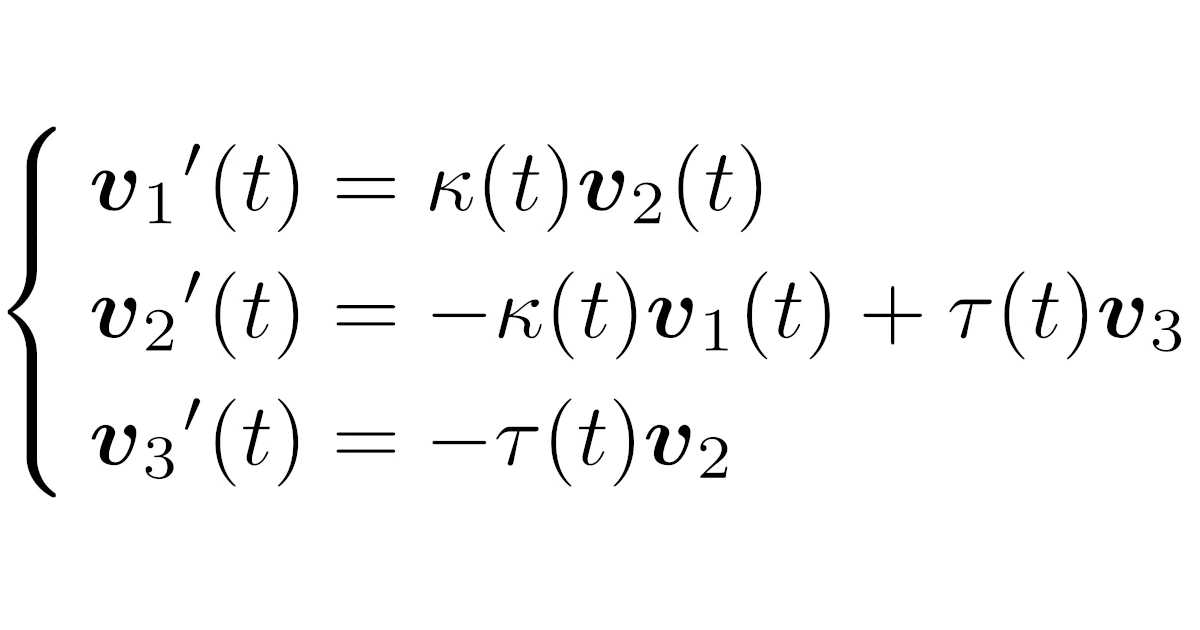
コメント