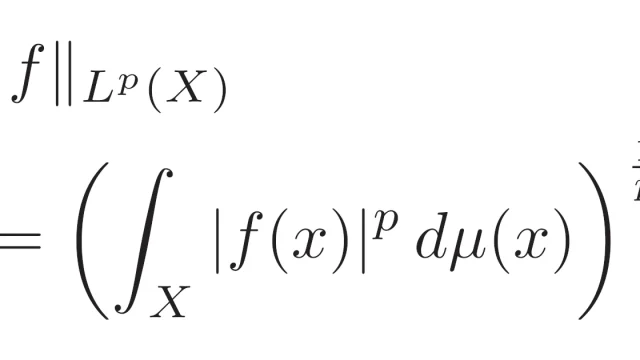 ルベーグ空間
ルベーグ空間 ルベーグ空間(Lᵖ空間)|ルベーグ積分に関するノルム・内積
測度空間Xに対して,Xでp乗可積分な関数の(商)空間をLᵖ(X)と表します.この記事ではLᵖ(X)の正確な定義を説明し,LᵖノルムによってLᵖ(X)がノルム空間・内積空間となることを解説します.
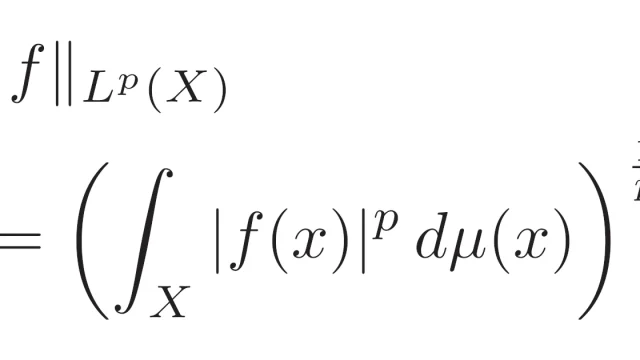 ルベーグ空間
ルベーグ空間 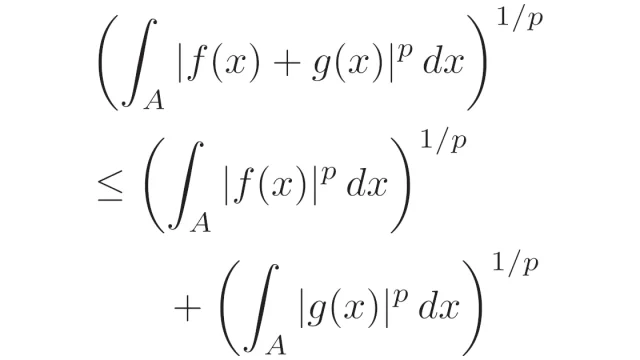 ルベーグ空間
ルベーグ空間 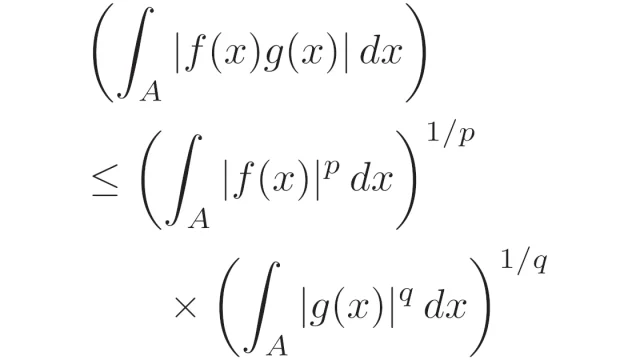 ルベーグ空間
ルベーグ空間 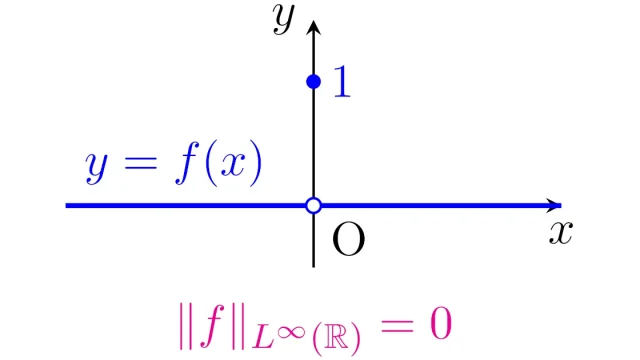 ルベーグ空間
ルベーグ空間 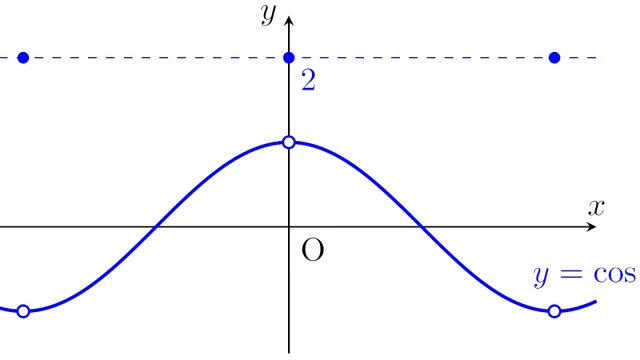 ルベーグ空間
ルベーグ空間 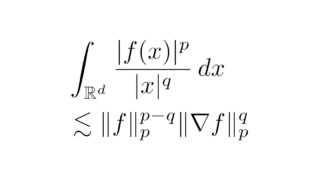 関数空間
関数空間 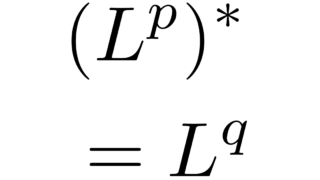 関数空間
関数空間  関数空間
関数空間