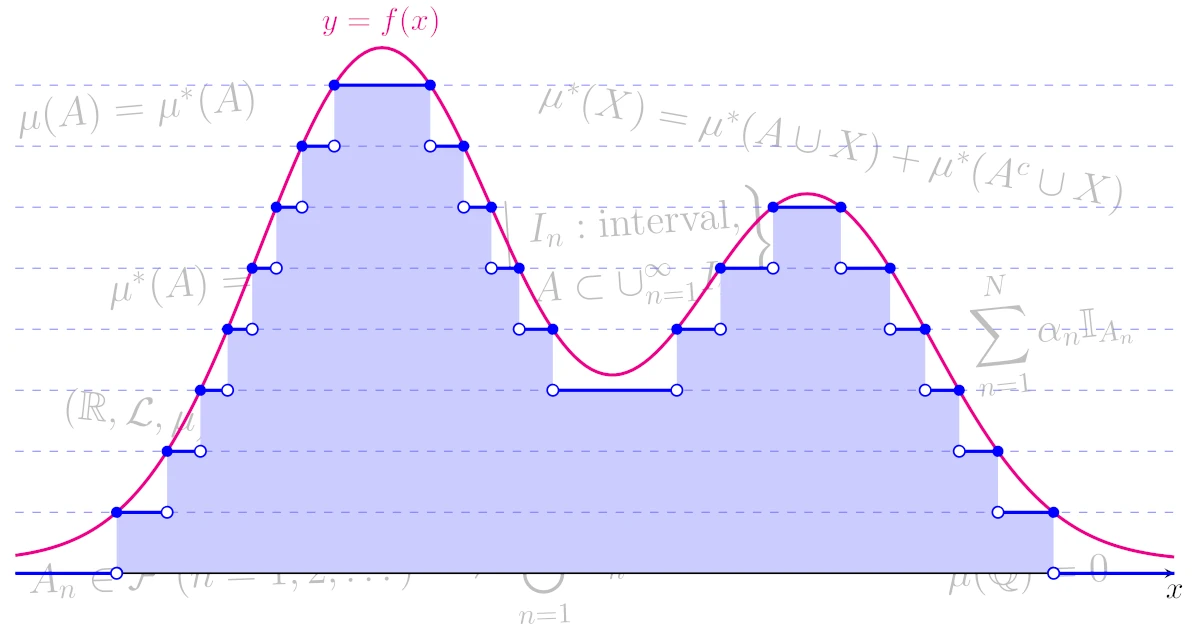
高校数学で積分を学んで「こんな曲がった境界の図形の面積が求められるのか！」と驚いた経験をもつ方は多いのではないでしょうか．
さらに，大学に進んで微分積分学を学ばれた方は厳密にリーマン積分と呼ばれる積分を学びます．多くの人はリーマン積分で十分ですが，実はその先にルベーグ積分と呼ばれる積分があります．
ルベーグ積分は単に面積を求めるための道具に留まらず，確率論や統計学の基礎となっている測度論と本質的に関わる重要な積分となっています．
オンラインセミナー【ゼロから始める確率論・統計学とルベーグ積分】では
- ルベーグ積分がどのような積分か学びたい！
- ルベーグ積分が確率論や統計学とどのように関係しているのか学びたい！
- 測度論の確率論や統計学への応用を具体的に知りたい！
という方向けにルベーグ積分と測度論の基礎を解説します．
Zoomを用いたオンラインセミナーなので，Zoomが使える端末をお持ちであれば受講することができます．
また，録画と板書を共有フォルダにアップロードするので，リアルタイムでなくても自分の時間が合う時に受講することができます．
講師紹介
数学講師の山本拓人と申します．これまで私は
- 社会人向けの数学教室の講師
- 予備校講師・塾講師・家庭教師
- 映像授業による指導
- 高校数学・大学数学の教材作成
- 大手出版社での教科書系動画教材の校正
など，主に動画コンテンツやリアルタイム教育に様々な角度から１０年以上数学の指導を行ってきました．
この経験から「受講生の側に立ち状況ごとに適切な内容を選択する柔軟なスタイルの授業運営」のスキルはかなりものもだと自負しています．
現在の教育活動
- オンライン家庭教師
- 社会人向け数学教室講師
- 数学系ブロガー（閲覧数月１０万以上）
- 大学数学系YouTuber（チャンネル登録７０００人以上）
実績
- 元予備校講師．現在はオンライン家庭教師を行なっている他，社会人向け数学教室「すうがくぶんか」で集団授業の講師を務める．個別の体験授業を受講した方の９０%以上が入会しており，これまでリアルタイムの（集団・個別）授業で指導してきた受講生は１０００人以上．
- 予備校講師初年度から予備校の生徒アンケートで抜群の成績を残し通常の８倍の報酬アップを提示されるなど，早い段階から数学講師として頭角を表す．
- 大学受験解説ブログ・大学数学解説ブログにて解説記事を執筆しており，検索上位の記事も多数．
- YouTube全動画の再生回数は１６３万回以上（２０２４年９月現在）．
- 大学院修士課程に飛び級で首席合格・首席修了するなど，数学に対する知識・理解も深い．専門は非線形偏微分方程式論．
- 趣味はダーツ・麻雀・甘いもの食べ歩き．
セミナー内容
「確率論や統計学をきちんと学ぼうとしたが，「確率空間」「確率変数」といった用語を理解できなかった」
「教科書では定義や定理は載っていても直感的な考え方にまでは触れておらず，「結局何がやりたいの？」と困惑してしまう」
「丁寧にルベーグ積分から学ぼうとすると，果てしない道のりに絶望……」
こんな苦い経験をした方は少なくないでしょう．実際，私が指導してきた生徒さんの中にもそのような方々は多くいらっしゃいました．
そこで，今回のセミナーでは丁寧に進めることを重視して
- 第１回：ルベーグ積分の考え方の基礎を学ぶ
- 第２回：ルベーグ積分をもとにして測度論の考え方を学ぶ
- 第３回：確率論・統計学の確率変数を測度論の枠組みで扱う
の全３回で，ルベーグ積分をもとにして確率論・統計学を解説します．
第１回：ルベーグ積分の基礎を学ぶ
ルベーグ積分では「集合の長さ」が重要な役割を果たします．例えば，以下の階段状のグラフ$y=f(x)$に対して，水色部分の面積はどのように考えますか？
これは
- ２×（$f(x)=2$となる$x$の集合の長さ）
- ３×（$f(x)=3$となる$x$の集合の長さ）
- １×（$f(x)=1$となる$x$の集合の長さ）
の和と考えて，
と求められますね．
これは関数$f$のとる値１，２，３に注目した面積の考え方で，「集合の長さ」が面積を求める上でキーとなる量になっていますね．この考え方を階段状でない関数に対して考える積分がまさにルベーグ積分の基礎になっています．
第１回目の授業では
- 集合の長さ（外測度）の考え方
- ルベーグ測度の考え方と定義
- ルベーグ積分の定義と基本性質
を解説します．
第２回：ルベーグ積分をもとにして測度論の考え方を学ぶ
ルベーグ積分でキーとなる「集合の長さ」は「集合の要素の多さ」と考えることができます．
このルベーグ積分の考え方をより広く捉え直すことで，面積に留まらない様々な「量」を考えられるようになります．こうしてできる分野が測度論です．
例えば，確率論・統計学では何らかの事象が起こる割合を「量」と捉えることで，測度論の枠組みで確率論・統計学を運用することができます．
第２回目の授業では
- 可測空間の定義・直感的な捉え方・具体例
- 測度空間の定義・直感的な捉え方・具体例
- 測度空間上の可測関数
を解説します．
第３回：確率論・統計学の確率変数を測度論の枠組みで扱う
確率論・統計学では確率変数が中心的な概念として扱われますが，確率変数がどういったものか最初はなかなか捉えづらく，実際多くの方が確率変数でつまずいてしまいます．
これは多くの教科書で，いくつかの有名な確率変数に限った説明のみに偏ってしまっていることが原因であることが多いです．
しかし，もっと簡単な例から確率変数の学び始めることで，ずっとラクに確率変数の考え方を理解できるようになります．
第３回目の授業では
- 簡単な例から確率変数の考え方を理解する
- 確率変数を測度論の枠組みで捉える
- 確率変数の期待値とルベーグ積分
を解説します．
こんな方にオススメ！
本講座は次のような人にオススメです！
- ルベーグ積分の考え方を知りたい人
- ルベーグ積分と測度論の関係を知りたい人
- 理論から確率論・統計学を学びたい人
- 確率論・統計学で使われる測度論の具体例を知りたい人
ルベーグ積分について詳しくは後続の別講座で解説するので，本講座ではルベーグ積分の理論にそこまで深くは立ち入りません．
ルベーグ積分の理論を詳しく知りたい方は開講予定の後続の講座をご受講ください．
前提知識
集合の書き方や和集合・共通部分などの基本的な集合の扱いを何となく知っておけば十分理解できるように説明します．
ルベーグ積分とリーマン積分は大きく異なる定義がされるので，微分積分学やリーマン積分を理解している必要はありません．
受講にあたって
以下の要領でセミナーを行います．
日時
以下の日時で開講します（いずれも１７：３０から１２０分）．
- １０月１２日（土）１７：３０〜１９：３０
- １０月１３日（日）１７：３０〜１９：３０
- １０月１４日（月祝）１７：３０〜１９：３０
場所と持ち物
Zoomを用いたオンラインセミナーです．そのためリアルタイムで参加される場合はZoomを使用できる機器をご準備ください．
必要なものは
- 筆記用具
- 板書（スライド）のメモをとるノート
です．
授業録画・板書の共有
授業の録画と板書を共有フォルダにアップロードします．
そのため，復習がしやすく，またリアルタイムで出席できない方も都合に合わせて受講することができます．
この録画と板書は半年間視聴できます．
※板書はダウンロード可能ですが，授業動画はダウンロード不可能です．
授業料
全３回で１６，５００円（税込）です．お支払いは銀行振込にてお願いします（手数料はご負担をお願い致します）．
振込先の銀行は
- 三井住友銀行
- 三菱URJ銀行
- みずほ銀行
から振込手数料などご都合の良い銀行をご指定ください．振込先の口座はお申し込み後にご連絡します．また，着金が確認できましたら領収書をお送りします．
お申し込み
受講を希望される方は以下の応募フォームから必要事項を送信してください．
ご案内を入力して頂いたアドレスにお送りします．