例えば,ある6面サイコロを振っていたところ出目が偏る気がしたので,本当に均等に目が出るサイコロなのかどうかを確かめたいとしましょう.通常のサイコロは
「全ての目が確率1/6で出る」
と想定されますが,この想定が誤りであることを確かめたいわけですね.
このことを確認する方法として,ピアソンのカイ二乗検定統計量を用いる仮説検定があります.
もう少し詳しく書けば,想定(帰無仮説)のもとで試行回数を大きくしていくとピアソンのカイ二乗検定統計量は漸近的にカイ二乗分布に従うことが証明でき,このことを用いた仮説検定をカイ二乗適合度検定(ピアソンのカイ二乗検定)といいます.
この記事では
- カイ二乗適合度検定の流れ
- ピアソンのカイ二乗検定統計量
を順に解説します.
カイ二乗適合度検定の流れ
正当化は後回しにして,まずはカイ二乗適合度検定の流れを解説します.
ここでは,冒頭の「ある6面サイコロを振っていたところ出目が偏る気がしたので,本当に均等に目が出るサイコロなのかどうかを確かめたい」という問題を考えましょう.
これを仮説検定の枠組みで書き直せば,帰無仮説$H_0$と対立仮説$H_1$を
- $H_0$:全ての目が確率1/6で出る
- $H_1$:いずれかの目が確率1/6で出ない
として,カイ二乗適合度検定を行いましょう.
ステップ1(それぞれのカテゴリーが生じた回数をカウントする)
まずは繰り返しサイコロを振って,6つの目がそれぞれ何回起こったかをカウントします.ここでは,200回サイコロを振って
- 1の目が49回
- 2の目が32回
- 3の目が22回
- 4の目が35回
- 5の目が29回
- 6の目が33回
出たとしましょう.
確かに1の目が多く出ているように思えますが,これがただの偏りなのか実際に1の目が出やすいのかを検定しようというのがここでの目標です.
経験的に(試行回数)×(帰無仮説での各カテゴリーの確率)が5以下の場合は,カイ二乗適合度検定で適切に検定できないとされています.いまは$200\times\frac{1}{6}>5$なので問題ありません.
ステップ2(ピアソンのカイ二乗検定統計量Qを計算する)
ピアソンのカイ二乗検定統計量$Q$は
- 観測度数(実際に観測した回数)を$O_i$
- 期待度数($H_0$が正しいとしたときの理論値)を$E_i$
を用いて,$Q=\sum\limits_{i=1}^{k}\dfrac{(O_i-E_i)^2}{E_i}$と定義されます($k$はカテゴリーの数).
いまカテゴリー数$k$は出目の個数の$k=6$で,$O_i$はステップ1で観測した回数,試行回数は200,$H_0$では全ての出目が確率1/6で出るので全ての$E_i$が$200\cdot\frac{1}{6}$です.よって,
\begin{align*}Q&=\frac{(49-200\cdot\frac{1}{6})^2}{200\cdot\frac{1}{6}}+\frac{(32-200\cdot\frac{1}{6})^2}{200\cdot\frac{1}{6}}+\frac{(22-200\cdot\frac{1}{6})^2}{200\cdot\frac{1}{6}}
\\&+\frac{(35-200\cdot\frac{1}{6})^2}{200\cdot\frac{1}{6}}+\frac{(29-200\cdot\frac{1}{6})^2}{200\cdot\frac{1}{6}}+\frac{(33-200\cdot\frac{1}{6})^2}{200\cdot\frac{1}{6}}
\\&=\frac{298}{25}=11.92\end{align*}
となります.
観測値と帰無仮説の当てはまりが良いほど$Q$は小さくなるのですが,今回は1の目が明確に多く出ていて帰無仮説$H_0$と大きくズレているので$Q$は大きめの値になっています.
ステップ3(Qがカイ二乗分布に従うとして検定を行う)
$k$カテゴリーある試行を十分多く繰り返したとき,ピアソンのカイ二乗検定統計量$Q$は帰無仮説のもとで$\chi^2(k-1)$(自由度が「カテゴリー数−1」のカイ二乗分布)に漸近的に従うことが証明されます.
今回のカテゴリー数は6なので,ピアソンのカイ二乗検定統計量$Q$は自由度5のカイ二乗分布$\chi^2(5)$に漸近的に従います.
自由度5のカイ二乗分布$\chi^2(5)$の有意水準0.05での臨界値は11.07なので,ステップ2で求めた$Q=11.92$がこれを超えているため帰無仮説$H_0$は棄却されます($p$値は0.036).
すなわち,サイコロの出目の偏りはたまたまではなく,実際に出目が均等でないサイコロだったと判断できます.
以上の検定方式をカイ二乗適合度検定といいます.
ピアソンのカイ二乗検定統計量
ピアソンのカイ二乗検定統計量$Q$の定義をして,$Q$が漸近的にカイ二乗分布に従うことを証明しましょう.
ピアソンのカイ二乗検定統計量の定義
起こる確率が$p_1,p_2,\dots,p_k$の$k$個のカテゴリーをもつ試行を$n$回行う多項分布を$\mrm{Mult}(n;p_1,p_2,\dots,p_k)$と表します.
$r_1,r_2,\dots,r_k$は和が1の正数とする($k\ge2$).$(X_1,X_2,\dots,X_k)\sim\mrm{Mult}(n;p_1,p_2,\dots,p_k)$に対して,
\begin{align*}Q(n;X_1,X_2,\dots,X_k)=\sum_{i=1}^{k}\frac{(X_i-nr_i)^2}{nr_i}\end{align*}
を,帰無仮説$H_0:p_1=r_1,p_2=r_2,\dots, p_k=r_k$のもとでのピアソンのカイ二乗検定統計量という.
もちろんカイ二乗適合度検定の流れで説明した$Q=\frac{(O_i-E_i)^2}{E_i}$と本質的に同じものです.$X_i$が観測度数$O_i$に対応し,$nq_i$が期待度数$E_i$に対応しています.
先ほどのカイ二乗適合度検定の流れの中で扱った例では,$k=6$で帰無仮説が
\begin{align*}H_0:p_1=\frac{1}{6},\dots,p_6=\frac{1}{6}\end{align*}
だったので,これは$r_1=\dots=r_6=\frac{1}{6}$ということですね.また,$n=200$なので
\begin{align*}Q(n;X_1,\dots,X_6)=\sum_{i=1}^{6}\frac{(X_i-200\cdot\frac{1}{6})^2}{200\cdot\frac{1}{6}}\end{align*}
となります.最後に,観測度数$X_i$を代入したものが$Q$だったわけですね.
カイ二乗検定統計量は漸近的にカイ二乗分布に従う
カイ二乗適合度検定ができるためのキーとなる定理が次の定理です.
帰無仮説$H_0:p_1=r_1,p_2=r_2,\dots, p_k=r_k$のもとでピアソンのカイ二乗検定統計量は,
\begin{align*}Q(n;X_1,X_2,\dots,X_k)\xrightarrow[]{n\to\infty}_{d}\chi^2(k-1)\end{align*}
と分布収束する.
この定理によって,十分な試行回数のもとピアソンのカイ二乗検定統計量$Q$をカイ二乗分布で検定できるわけですね.
経験的には,全ての$k$に対して$nr_k>5$であれば,カイ二乗適合度検定は十分機能するようです.
カイ二乗検定統計量がカイ二乗分布に漸近的に従うことの証明の準備
定理の証明のためにいくつか補題を用意しておきましょう.
補題1(多項分布の書き換え)
二項分布$\mrm{Bin}(n,p)$に従う確率変数$X$が,試行回数1回の二項分布$\mrm{Bin}(1,p)$(ベルヌーイ分布$\mrm{Ber}(p)$)に独立に従う確率変数$X_1,X_2,\dots,X_n$で
\begin{align*}X=X_1+X_2+\dots+X_n\end{align*}
と表すことができるのでした.

これと同様に多項分布に従う確率変数ベクトルも,試行回数1回の多項分布に独立に従う確率変数ベクトルの和で表すことができます.
$\m{X}\sim\mrm{Mult}(n;p_1,p_2,\dots,p_k)$と,独立な$\m{Y}_1,\m{Y}_2,\dots,\m{Y}_n\sim\mrm{Mult}(1;p_1,p_2,\dots,p_k)$に対して,
\begin{align*}\m{X}=\m{Y}_1+\m{Y}_2+\dots+\m{Y}_n\end{align*}
が成り立つ.
補題2(多変量の中心極限定理)
1次元の確率変数の中心極限定理と同様に,確率変数ベクトルに対しても中心極限定理が成り立ちます.
$m$次元確率変数ベクトル$\m{Y}_1,\m{Y}_2,\dots,\m{Y}_n$は独立同分布(平均$\m{\mu}$,分散共分散行列$\Sigma$)に従うとし,$\m{Y}_1,\m{Y}_2,\dots,\m{Y}_n$の標本平均を$\overline{\m{Y}}_n$とする:
\begin{align*}\overline{\m{Y}}_n=\frac{\m{Y}_1+\m{Y}_2+\dots+\m{Y}_n}{n}.\end{align*}
このとき,$\sqrt{n}\bra{\overline{\m{Y}}_n-\m{\mu}}$は$n\to\infty$のとき漸近的に$N_{m}(\m{0},\Sigma)$に従う(分布収束).
補題3(カイ二乗分布に従う2次形式)
多変量正規分布に従う確率変数$\m{X}$について,うまく2次形式を考えるとカイ二乗分布に従う確率変数となります.
$\m{Z}\sim N_{m}(\m{\mu},\Sigma)$に対して
\begin{align*}(\m{Z}-\m{\mu})^T\Sigma^{-1}(\m{Z}-\m{\mu})\sim\chi^2(m)\end{align*}
が成り立つ.
$Q(n;X_1,X_2,\dots,X_k)$の収束の証明では$\mu=\m{0}$の場合を用います.すなわち,$\m{Z}\sim N_{m}(\m{0},\Sigma)$に対して
\begin{align*}\m{Z}^T\Sigma^{-1}\m{Z}\sim\chi^2(m)\end{align*}
が成り立つことを用います.
一般に,$\m{x}\in\R^m$と$m$次正方行列$A$に対して,$\m{x}^TA\m{x}$はスカラーとなり,この形の式を2次形式といいますね.
カイ二乗検定統計量がカイ二乗分布に漸近的に従うことの証明
それでは目標の定理を証明しましょう.
(再掲)帰無仮説$H_0:p_1=r_1,p_2=r_2,\dots, p_k=r_k$のもとでピアソンのカイ二乗検定統計量は,
\begin{align*}Q(n;X_1,X_2,\dots,X_k)\xrightarrow[]{n\to\infty}_{d}\chi^2(k-1)\end{align*}
と分布収束する.
確率変数ベクトル$\m{Z}$と行列$A$の定義
証明の中で重要となる$\m{Z}$と$A$を次のように定める.$\ell\in\{1,2,\dots,k-1\}$に対して
\begin{align*}Z_\ell=\sqrt{n}\bra{\frac{X_\ell}{n}-r_\ell}\end{align*}
とおき,$i,j\in\{1,2,\dots,k-1\}$に対して
\begin{align*}a_{i,j}=\begin{cases}\frac{1}{r_k}+\frac{1}{r_i}&(i=j)\\\frac{1}{r_k}&(i\neq j)\end{cases}\end{align*}
とおいて,
- $(k-1)$次確率変数ベクトル$\m{Z}$を$\m{Z}=\sbmat{Z_1\\\vdots\\Z_{k-1}}$
- $(k-1)$次正方行列$A$を$A=(a_{i,j})$
で定める.
$Q(X_1,X_2,\dots,X_k)=\m{Z}^{T}A\m{Z}$の証明
$X_1+X_2+\dots+X_k=n$, $r_1+r_2+\dots+r_k=1$だから,ピアソンのカイ二乗検定統計量
\begin{align*}Q(n;X_1,X_2,\dots,X_k)=\sum\limits_{i=1}^{k}\frac{(X_i-nr_i)^2}{nr_i}\end{align*}
の最後の第$k$項は
\begin{align*}\frac{(X_k-nr_k)^2}{nr_k}
&=\frac{\{(n-X_1-\dots-X_{k-1})-n(1-r_1-\dots-r_{k-1})\}^2}{nr_k}
\\&=\frac{\{(X_1-nr_1)+\dots+(X_{k-1}-nr_{k-1})\}^2}{nr_k}
\\&=\sum_{i=1}^{k-1}\frac{(X_i-nr_i)^2}{nr_k}+\sum_{\substack{i,j=1\\i\neq j}}^{k-1}\frac{(X_i-nr_i)(X_j-nr_j)}{nr_k}\end{align*}
となる.よって,
\begin{align*}&Q(n;X_1,X_2,\dots,X_k)
\\&=\frac{(X_k-nr_k)^2}{nr_k}+\sum_{i=1}^{k-1}\frac{(X_i-nr_i)^2}{nr_i}
\\&=\sum_{i=1}^{k-1}\bra{\frac{1}{nr_k}+\frac{1}{nr_i}}(X_i-nr_i)^2+\sum_{\substack{i,j=1\\i\neq j}}^{k-1}\frac{(X_i-nr_i)(X_j-nr_j)}{nr_k}
\\&=n\sum_{i=1}^{k-1}\bra{\frac{1}{r_k}+\frac{1}{r_i}}\bra{\frac{X_i}{n}-r_i}^2+n\sum_{\substack{i,j=1\\i\neq j}}^{k-1}\frac{1}{r_k}\bra{\frac{X_i}{n}-r_i}\bra{\frac{X_j}{n}-r_j}
\\&=\sum_{i=1}^{k-1}a_{i,i}Z_i^2+\sum_{\substack{i,j=1\\i\neq j}}^{k-1}a_{i,j}Z_iZ_j
=\sum_{i,j=1}^{k-1}a_{i,j}Z_iZ_j
=\m{Z}^TA\m{Z}\end{align*}
が成り立つ.
$\m{Z}$が$n\to\infty$で漸近的に正規分布に従うことの証明
補題1より,独立な$\m{Y}_1,\m{Y}_2,\dots,\m{Y}_n\sim\mrm{Mult}(1;p_1,p_2,\dots,p_k)$により
\begin{align*}\sbmat{X_1\\\vdots\\X_k}=\m{Y}_1+\m{Y}_2+\dots+\m{Y}_n\end{align*}
が成り立つ.多項分布の性質から,各$\ell\in\{1,2,\dots,k-1\}$に対して,$E[\m{Y}_\ell]=\m{r}$であり,
\begin{align*}\sigma_{i,j}=\begin{cases}r_{i}(1-r_{i})&(i=j)\\-r_{i}r_{j}&(i\neq j)\end{cases}\end{align*}
とおくと$\Sigma:=V[\m{Y}_\ell]=(\sigma_{i,j})$である.
ここで,$\m{Y}_1,\m{Y}_2,\dots,\m{Y}_n$の標本平均を$\overline{\m{Y}}_n$とすると
\begin{align*}\overline{\m{Y}}_n=\frac{\m{Y}_1+\m{Y}_2+\dots+\m{Y}_n}{n}=\sbmat{X_1/n\\\vdots\\X_k/n}\end{align*}
となり,さらに$\m{r}=\sbmat{r_1\\\vdots\\r_{k-1}}$とおくと
\begin{align*}\m{Z}=\sqrt{n}(\overline{\m{Y}}_n-\m{r})\end{align*}
である.よって,多変量の中心極限定理(補題2)より$\m{Z}$は漸近的に$(k-1)$次元正規分布$N_{k-1}(0,\Sigma)$に従う(分布収束).
$A=\Sigma^{-1}$の証明
$r_1+r_2+\dots+r_k=1$に注意する.任意の$i\in\{1,2,\dots,k-1\}$に対して,$A\Sigma$の第$(i,i)$成分は
\begin{align*}&\sum_{m=1}^{k-1}a_{i,m}\sigma_{m,i}=a_{i,i}\sigma_{i,i}+\sum_{\substack{m=1\\m\neq i}}^{k-1}a_{i,m}\sigma_{m,i}
\\&=\bra{\frac{1}{r_k}+\frac{1}{r_i}}\cdot r_i(1-r_i)+\sum_{\substack{m=1\\m\neq i}}^{k-1}\frac{-r_mr_i}{r_k}
\\&=\frac{r_i(1-r_i)}{r_k}+(1-r_i)-\frac{r_i}{r_k}\sum_{\substack{m=1\\m\neq i}}^{k-1}r_m
\\&=\frac{r_i(1-r_i)}{r_k}+(1-r_i)-\frac{r_i}{r_k}(1-r_i-r_k)=1\end{align*}
である.また,任意の異なる$i,j\in\{1,2,\dots,k-1\}$に対して,$A\Sigma$の第$(i,j)$成分は
\begin{align*}&\sum_{m=1}^{k-1}a_{i,m}\sigma_{m,j}=a_{i,i}\sigma_{i,j}+a_{i,j}\sigma_{j,j}+\sum_{\substack{m=1\\m\neq i,j}}^{k-1}a_{i,m}\sigma_{m,j}
\\&=\bra{\frac{1}{r_k}+\frac{1}{r_i}}(-r_ir_j)+\frac{r_j(1-r_j)}{r_k}+\sum_{\substack{m=1\\m\neq i}}^{k-1}\frac{-r_mr_j}{r_k}
\\&=-\frac{r_ir_j}{r_k}-r_j+\frac{r_j(1-r_j)}{r_k}-\frac{r_j}{r_k}\sum_{\substack{m=1\\m\neq i,j}}^{k-1}r_m
\\&=-\frac{r_ir_j}{r_k}-r_j+\frac{r_j(1-r_j)}{r_k}-\frac{r_j}{r_k}(1-r_i-r_j-r_k)=0\end{align*}
である.よって,$A\Sigma=I_{k-1}$が従う.
一般に,$n$次正方行列$A,B$が$AB=I_n$を満たせば,$A$(と$B$)は正則行列で$A=B^{-1}$を満たすので,$A=\Sigma^{-1}$が成り立つ.
$Q(X_1,X_2,\dots,X_k)\xrightarrow[]{n\to\infty}_{d}\chi^2(k-1)$の証明
$Q(n;X_1,X_2,\dots,X_k)=\m{Z}^TA\m{Z}$と$A=\Sigma^{-1}$より
\begin{align*}Q(n;X_1,X_2,\dots,X_k)=\m{Z}^T\Sigma^{-1}\m{Z}\end{align*}
である.$\m{Z}$は漸近的に$(k-1)$次元正規分布$N_{k-1}(0,\Sigma)$に従う(分布収束)から,連続写像定理と補題3を併せて,
\begin{align*}Q(X_1,X_2,\dots,X_k)\xrightarrow[]{n\to\infty}_{d}\chi^2(k-1)\end{align*}が成り立つ.

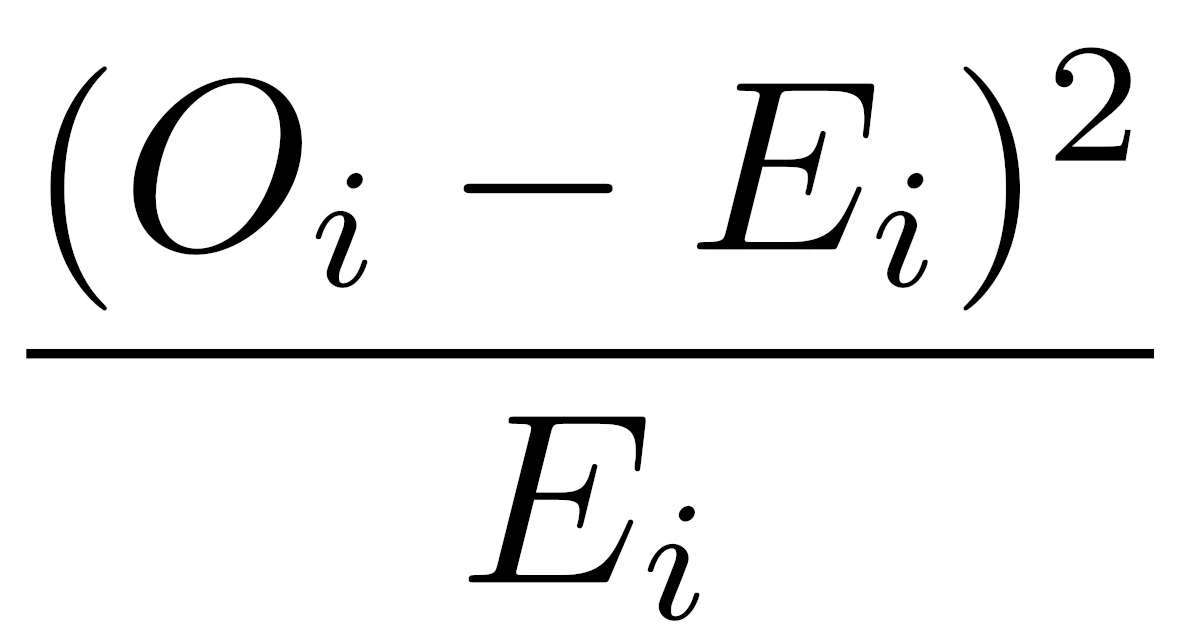
コメント