例えば,
- 任意の整数$n$に対して,$2n$は偶数である
- ある実数$x$が存在して,$x^2+x-1=0$が成り立つ
など,数学(数理論理学)には「任意の〜に対して」「ある〜が存在して」という言い回しがよく用いられます.
そこで,これらを表す記号として
- 全称記号∀
- 存在記号∃
があり,これらを用いることで数学の主張をシンプルに表すことができます.これらは慣れてしまえばとても便利なので,ぜひ使えるようになっておきたい記号たちです.
この記事では
- ∀,∃の意味と読み方
- ∀,∃の使い方の具体例
- ∀,∃の順番の注意点
を順に解説します.
∀,∃の意味と読み方
この記事のタイトルにもあるように
- ∀には全称記号
- ∃には存在記号
という名前がついています.
$\sqrt{\quad}$に根号という名前がついているようなものですね.
全称記号∀は「どんな〜に対しても」
全称記号∀は全ての対象を指す記号で「どんな〜に対しても」「全ての〜に対して」「任意の〜に対して」という意味を持っています.
例えば
\begin{align*}\forall x>0\quad -x<0\end{align*}
と書くと,これは
- 任意の正の数$x$に対して,$-x$は負の数である
- 0より大きい任意の実数$x$に対して,$-x$は0より小さい
などと読むことになります.
英語では“For all x>0, it holds that $-x<0$.”などとなります.
全称記号∀はアルファベットのAを180°回転させたもので,ここでのAは
- 「どんな」という意味の英単語“any”
- 「全ての」という意味の英単語“all”
- 「任意の」という意味の英単語“arbitrary”
の頭文字に由来しています.
存在記号∃は「ある〜が存在する」
存在記号∃は存在を表す記号で「ある〜が存在する」という意味を持っており,何らかの条件をつか加えることが多く”s.t.”とともに用いられます.
例えば
\begin{align*}\exists x>0\quad \text{s.t.}\quad x>10000\end{align*}
と書くと,これは
- ある正の数$x$が存在して,$x>10000$が成り立つ
- $x>10000$を満たす正の数$x$が存在する
などと読むことになります.
英語では“There exists x>0 such that it holds that $x>10000$.”などとなります.“s.t.”は英語の“〜such that …”(…を満たす〜)の略です.
もしかすると,多くの人にとっては「ある〜が存在して……が成り立つ」よりも「……を満たす〜が存在する」の方が読みやすいかも知れません.
しかし,この記事の最後の注意2で説明するように,「……を満たす〜が存在する」という表現は誤解を生むことがあるので,「ある〜が存在して……が成り立つ」という表現に慣れておきたいところです.
存在記号∃はアルファベットのEを180°回転させたもので,ここでのEは「存在する」という意味の英単語“exist”に由来しています.また,
- 一意に存在する場合は$\exists!$や$\exists1$
- 存在しない場合は$\not\exists$
などと表します.
∀,∃の使い方の具体例
具体的に全称記号∀と存在記号∃の使い方を見てみましょう.
例1(全称記号∀)
命題「任意の実数$x$に対して,$x^2+2x+1\ge0$が成り立つ」を全称記号∀,存在記号∃を用いて表せ.
一般に実数全部の集合(数直線)は$\R$を用いて表すので,「実数$x$」は$x\in\R$と表せる.
また,「任意の〜に対して」は全称記号∀を用いて表せるので
\begin{align*}\forall x\in\R\quad x^2+2x+1\ge0\end{align*}
である.
例2(存在記号∃)
命題「ある実数$x$が存在して,$x^2=3$が成り立つ」を全称記号∀,存在記号∃を用いて表せ.
この命題の$x$は$\pm\sqrt{3}$のことですね.
一般に実数全部の集合(数直線)は$\R$を用いて表すので,「実数$x$」は$x\in\R$と表せる.
「ある〜が存在して……が成り立つ」は存在記号∃と s.t. を用いて表せるので,
\begin{align*}\forall x\in\R\quad\text{s.t.}\quad x^2=3\end{align*}
である.
例3(全称記号∀と存在記号∃)
命題「任意の$x\in\R$に対して,ある$y\in\R$が存在して,$x+y=0$が成り立つ」を全称記号∀,存在記号∃を用いて表せ.
この命題の$y$は$x$の逆数のことですね.
「任意の〜に対して」は全称記号を用いて表せ,「ある〜が存在して……が成り立つ」は存在記号∃とs.t.を用いて表せるので,
\begin{align*}\forall x\in\R\quad[\exists y\in\R\quad\text{s.t.}\quad x+y=0]\end{align*}
である.
全称記号∀,存在記号∃は前から読む決まりなので,かっこ[ ]はなくても構いません.つまり,
\begin{align*}\forall x\in\R\quad\exists y\in\R\quad\text{s.t.}\quad x+y=0\end{align*}
と書いても構いません.
例4(存在記号∃と全称記号∀)
命題「ある$x\in\R$が存在して,任意の$y\in\R$が存在して,$x\cdot y=y$が成り立つ」を全称記号∀,存在記号∃を用いて表せ.
この命題の$x$は1のことですね.
「ある〜が存在して……が成り立つ」は存在記号∃とs.t.を用いて表せ,「任意の〜に対して」は全称記号を用いて表せるので,
\begin{align*}\exists x\in\R\quad\text{s.t.}\quad[\forall y\in\R\quad x\cdot y=y]\end{align*}
である.
全称記号∀,存在記号∃は前から読む決まりなので,かっこ[ ]はなくても構いません.つまり,
\begin{align*}\exists x\in\R\quad\text{s.t.}\quad\forall y\in\R\quad x\cdot y=y\end{align*}
と書いても構いません.
例5(ε-N論法)
数列の収束のε-N論法による定義は全称記号∀,存在記号∃を用いて表すことも多いですね.
$\{a_n\}$を実数列とし,$\alpha\in\R$とする.
命題「任意の$\epsilon>0$に対して,ある$N\in\N$が存在して,$n>N$なら$|a_n-\alpha|<\epsilon$が成り立つ」を全称記号∀,存在記号∃を用いて表せ.
$\N$は正の整数全部の集合ですね.
「任意の〜に対して」は全称記号を用いて表せ,「ある〜が存在して……が成り立つ」は存在記号∃とs.t.を用いて表せるので,
\begin{align*}\forall \epsilon>0\quad\exists N\in\N\quad\text{s.t.}\quad n>N\Ra|a_n-\alpha|<\epsilon\end{align*}
である.
個人的な見解ですが,微分積分学で$\epsilon\text{-}N$論法を学ぶのは,全称と存在の扱いに慣れるためだと思っています.
∀,∃の順番の注意点
2つ注意点があります.
注意1(∀,∃の順番の入れ替え)
全称記号∀,存在記号∃は順番を入れ替えると違う意味になってしまうことが多いです.
例えば,上の例3で扱った命題
\begin{align*}\forall x\in\R\quad[\exists y\in\R\quad\text{s.t.}\quad x+y=0]\quad\dots(*)\end{align*}
と,$\forall x\in\R$と$\exists y\in\R$を入れ替えてできる命題
\begin{align*}\exists y\in\R\quad\text{s.t.}\quad[\forall x\in\R\quad x+y=0]\quad\dots(**)\end{align*}
を比べてみましょう.
まず,命題$(*)$の$y$は$x$の後にあるため「$x$を見てから,$x+y=0$を満たす$y$をとれる」という主張になっています.
一方,命題$(**)$の$y$は$x$の前にあるため「$x$によらない万能な$y$がとれて,どんな$x$に対しても$x+y=0$が成り立つ」という主張になっており,確かに違う意味になっていますね.
なお,命題$(*)$は真で,命題$(**)$は偽なので,真偽も異なっていますね.
注意2(存在記号∃の読み方)
先ほど存在記号∃は
- 「ある〜が存在して……が成り立つ」
- 「……を満たす〜が存在する」
の読み方ができることを説明した際に,(2)では誤解が生じるため(1)の方が好ましいことに触れました.
例えば,上の例3で扱った命題
\begin{align*}\forall x\in\R\quad\exists y\in\R\quad\text{s.t.}\quad x+y=0\end{align*}
の$y$の存在を「……を満たす〜が存在する」で表現すると
「任意の$x\in\R$に対して$x+y=0$を満たす$y\in\R$が存在する」
となります.しかし,この表現では
- 『任意の$x\in\R$に対して$x+y=0$』を満たす$y\in\R$が存在する
- 任意の$x\in\R$に対して『$x+y=0$を満たす$y\in\R$が存在する』
のどちらなのか区別がつかず,
- 前者は$\exists y\in\R\quad\text{s.t.}\quad\forall x\in\R\quad x+y=0$
- 後者は$\forall x\in\R\quad\exists y\in\R\quad\text{s.t.}\quad x+y=0$
ですから,上の注意1で見たように意味が違ってきますね.
このように「……を満たす〜が存在する」の書き方は全称と併せたときに複数の解釈ができてしまうため,避けるのが無難だというわけですね.
一方,「ある〜が存在して……が成り立つ」は文字の登場順に読んでいるので,誤解のおそれがないわけですね.

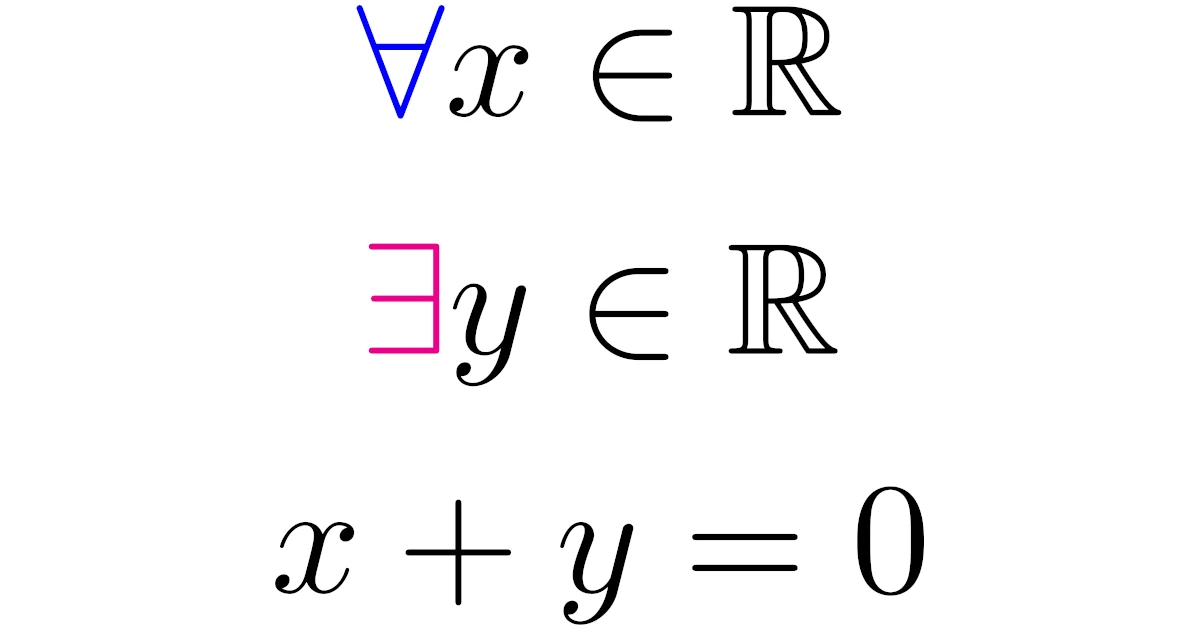
コメント