高校数学では，実数$x$を超えない最大の整数を$[x]$で表し，この$[\cdot]$をガウス記号と呼びました．
実はその実数を超えない最大の整数を返す関数は床関数と呼ばれており，$\lfloor{\cdot}\rfloor$で表すこともよくあります．
また，実数$x$以上の最小の整数を$\lceil{x}\rceil$で表し，この$\lceil{\cdot}\rceil$を天井関数と呼びます．
この記事では
- 床関数の定義と具体例と性質
- 天井関数の定義と具体例と性質
を順に解説します．
床関数（ガウス記号）
まずは床関数から解説します．
床関数の定義
実数$x$に対して，$x$以下の最大の整数を返す関数
を床関数（floor function）という．
$\R$は実数全部の集合，$\Z$は整数全部の集合なのでした．
高校数学では「$x$を超えない最大の整数を$[x]$と表し，$[\cdot]$をガウス記号という」と定義されますが，「$x$を超えない」というのは「$x$以下の」と同じですから，$[x]=\lfloor{x}\rfloor$が成り立ちますね．
なお，この「ガウス記号」という呼び名はガウスが平方剰余の相互法則を証明する論文の中で使われたことに由来するようです．この論文の中では
per signum $[x]$ exprimemus integrum ipsa $x$ proxime minorem, ita ut $x-[x]$ semper fiat quantitas positiva limites 0 et 1 sita.
と$[x]$が定義されています．
ざっと訳すなら「記号$[x]$は小さい方から$x$自身を近似する整数を表し，このとき$x-[x]$は０と１の間に制限された正の量となる」となります．
床関数の具体例とグラフ
気を付けたいのは$x$が負のときと整数のときの$\lfloor{x}\rfloor$です．
次のそれぞれの値を答えよ．
それぞれ次の通りである：
$\lfloor{2.5}\rfloor=2$と$\lfloor{\pi}\rfloor$は大丈夫でしょう（円周率$\pi$は$\pi=3.14\dots$ですね）．
$\lfloor{-2.5}\rfloor$については，$-2.5$以下の整数は$\dots,-5,-4,-3$であり，$-2$は$-2.5$以下ではないことに注意してください．よって，$-2.5$以下の最大の整数は$-3$ですね．
また，$x$が整数であれば$x$以下の最大の整数は$x$自身ですから，床関数$\lfloor{x}\rfloor=x$となりますね．
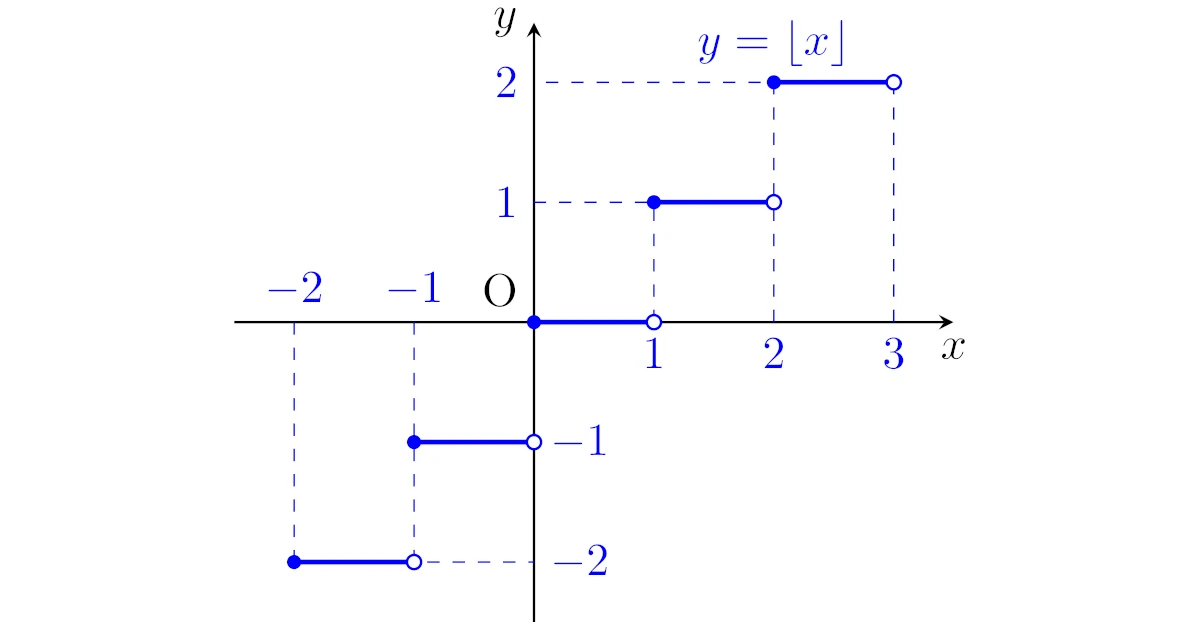
このように各実数$x$での$\lfloor{x}\rfloor$を考えていけば，$y=\lfloor{x}\rfloor$のグラフは以下のようになりますね．
床関数の性質
床関数の性質としては次はよく用いられます．
床関数について次が成り立つ．
- 実数$x$に対して$x-1<\lfloor{x}\rfloor\le x$
- 実数$x$と整数$n$に対して$\lfloor{x+n}\rfloor=\lfloor{x}\rfloor+n$
- 実数$x,y$に対して$\lfloor{x+y}\rfloor$は$\lfloor{x}\rfloor+\lfloor{y}\rfloor$または$\lfloor{x}\rfloor+\lfloor{y}\rfloor+1$に等しい．
(1)は$0\le x-\lfloor{x}\rfloor<1$の形で用いることもよくあります．
(2)で$x=0$とすれば整数$n$に対して$\lfloor{n}\rfloor=n$となることが分かりますね．上の具体例でも説明したように，このことも当たり前にしておきましょう．
(3)から$\lfloor{x}\rfloor+\lfloor{y}\rfloor\le\lfloor{x+y}\rfloor$が成り立つことが分かりますが，このように関数$f$が$f(x)+f(y)\le f(x+y)$を満たすとき$f$は優加法性をもつといいます．
(1) 定義より$\lfloor{x}\rfloor$は$x$以下だから$\lfloor{x}\rfloor\le x$である．
また，$x-(x-1)=1$より$x-1<n\le x$なる整数$n$が存在するから，$x-1<\lfloor{x}\rfloor$である．
(2) (1)より$x=\lfloor{x}\rfloor+r$（$0\le r<1$）と表せ，このとき
となる．$\lfloor{x}\rfloor+n$は整数だから，$0\le r<1$と併せると$x+n$以下の最大の整数は$\lfloor{x}\rfloor+n$である．
すなわち，$\lfloor{x+n}\rfloor=\lfloor{x}\rfloor+n$である．
(3) (1)より$x=\lfloor{x}\rfloor+r$（$0\le r<1$），$y=\lfloor{y}\rfloor+r’$（$0\le r'<1$）と表せ，このとき
となる．$\lfloor{x}\rfloor+\lfloor{y}\rfloor$は整数だから，$0\le r+r'<2$と併せると$x+y$以下の最大の整数は$\lfloor{x}\rfloor+\lfloor{y}\rfloor$または$\lfloor{x}\rfloor+\lfloor{y}\rfloor+1$である．
すなわち，$\lfloor{x+y}\rfloor=\lfloor{x}\rfloor+\lfloor{y}\rfloor,\lfloor{x}\rfloor+\lfloor{y}\rfloor+1$である．
天井関数
次に天井関数を解説しますが，考え方は床関数と同様です．
天井関数の定義
実数$x$に対して，$x$以上の最小の整数を返す関数
を天井関数（ceiling function）という．
「$x$を下回らない最小の整数」といってもいいですね．
天井関数の具体例とグラフ
次のそれぞれの値を答えよ．
それぞれ次の通りである：
各実数$x$での$\lceil{x}\rceil$を考えていけば，$y=\lceil{x}\rceil$のグラフは以下のようになりますね．
天井関数の性質
天井関数でも上でみた床関数に対応する性質が成り立ちます．
天井関数について次が成り立つ．
- 実数$x$に対して$x\le\lceil{x}\rceil<x+1$
- 実数$x$と整数$n$に対して$\lceil{x+n}\rceil=\lceil{x}\rceil+n$
- 実数$x,y$に対して$\lceil{x+y}\rceil$は$\lceil{x}\rceil+\lceil{y}\rceil$または$\lceil{x}\rceil+\lceil{y}\rceil-1$に等しい．
(1)は$0\le\lceil{x}\rceil-x<1$の形で用いることもよくあります．
(2)で$x=0$とすれば，天井関数と同様に整数$n$に対して$\lceil{n}\rceil=n$となることが分かりますね．
(3)から$\lceil{x+y}\rceil\le\lceil{x}\rceil+\lceil{y}\rceil$が成り立つことが分かりますが，このように関数$f$が$f(x+y)\le f(x)+f(y)$を満たすとき$f$は劣加法性をもつといいます．
(1) 定義より$\lceil{x}\rceil$は$x$以上だから$x\le\lceil{x}\rceil$である．
また，$(x+1)-x=1$より$x\le n<x+1$なる整数$n$が存在するから，$\lceil{x}\rceil<x+1$である．
(2) (1)より$x=\lceil{x}\rceil-r$（$0\le r<1$）と表せ，このとき
となる．$\lceil{x}\rceil+n$は整数だから，$0\le r<1$と併せると$x+n$以上の最小の整数は$\lceil{x}\rceil+n$である．
すなわち，$\lceil{x+n}\rceil=\lceil{x}\rceil+n$である．
(3) (1)より$x=\lceil{x}\rceil-r$（$0\le r<1$），$y=\lceil{y}\rceil-r’$（$0\le r'<1$）と表せ，このとき
となる．$\lceil{x}\rceil+\lceil{y}\rceil$は整数だから，$0\le r+r'<2$と併せると$x+y$以上の最小の整数は$\lceil{x}\rceil+\lceil{y}\rceil$または$\lceil{x}\rceil+\lceil{y}\rceil-1$である．
すなわち，$\lceil{x+y}\rceil=\lceil{x}\rceil+\lceil{y}\rceil,\lceil{x}\rceil+\lceil{y}\rceil-1$である．
コメント