例えば,群$(\Z,+)$について,2と−2を繰り返し演算することで,
\begin{align*}\dots,-6,-4,-2,0,2,4,6,\dots\end{align*}
を作ることができます.いまの場合は偶数全部の集合$2\Z$ができ,$(2\Z,+)$はもとの群$(\Z,+)$の部分群になっています.
このように,群$(G,\cdot)$に対し,いくつかの$g_1,g_2,\dots,g_n\in G$とそれらの逆元を演算してできる元全部の集合は群$(G,\cdot)$の部分群になり,この群を$\{g_1,g_2,\dots,g_n\}$により生成される部分群といいます.
線形空間で考えた生成される線形部分空間の群論ver.です.
この記事では
- 生成される部分群の定義・具体例・可換条件
- 巡回群の定義・具体例
- 補題の証明
を順に解説します.
「群論の基本」の一連の記事
- 群と部分群
- 1 群の定義・考え方を具体例から解説
- 2 部分群の証明のテンプレを例題から理解する
- 3 生成される部分群・巡回群の定義と具体例 (今の記事)
- 剰余類とラグランジュの定理|部分群の位数(準備中)
- 可換群の剰余群を具体例から丁寧に理解する(準備中)
- 正規部分群は非可換群の剰余群で超重要(準備中)
- 群の準同型
- 群の準同型は群の演算を保つ大切な写像(準備中)
- 群の準同型の像Im(f)と核Ker(f)の定義と例題(準備中)
- 群の準同型定理の考え方を例題から掴む(準備中)
生成される部分群の定義・具体例・可換条件
生成される部分群を定義して,いくつか具体例を考えます.
生成される部分群とは,いくつかの元をもとにできる部分群
群の集合上のいくつかの元を自由に演算してできる元全部の集合は部分群となります(この補題の証明は記事の最後にします).
群$(G,\cdot)$と空でない部分集合$S\subset G$を考え,集合$S$の元とその逆元を自由に演算してできる元全部の集合を$H$とする.すなわち,複号任意で
\begin{align*}H:=\set{{g_1}^{\pm1}{g_2}^{\pm1}\dots {g_r}^{\pm1}}{\begin{gathered}g_1,g_2,\dots,g_r\in S\end{gathered}}\end{align*}
とする.このとき,$(H,\cdot)$は$(G,\cdot)$の部分群となる.
$g_1,g_2,\dots,g_r$には同じものがあっても構いません.
部分群$H$を生成される部分群といいます.
上の補題の部分群$H$を$S$により生成される部分群(generated subgroup)といい$\anb{S}$と表し,$S$を生成系といい,$S$の元を生成元という.
とくに$S$が有限集合のとき$\anb{S}$は有限生成であるといい,$S=\{g_1,g_2,\dots,g_n\}$のときは$\anb{S}$を$\anb{g_1,g_2,\dots,g_n}$とも表す.
具体例1(群$(\Z,+)$での$\anb{2}$)
$\Z$に通常の加法+の可換群$(\Z,+)$を考えます.
生成される部分群$\anb{2}$は2と−2(2の逆元)を自由に演算してできる整数全部の集合なので,
\begin{align*}\anb{2}=\{\dots,-6,-4,-2,0,2,4,6,\dots\}=2\Z\end{align*}
と偶数全部の集合になりますね.
同様に考えれば,任意の$k\in\Z$に対して,生成される部分群$\anb{k}$は$k$の倍数全部の集合$k\Z$です:
\begin{align*}\anb{k}=\{\dots,-3k,-2k,-k,0,k,2k,3k,\dots\}=k\Z.\end{align*}
具体例2(群$(\R_+,\cdot)$での$\langle2,\sqrt{3}\rangle$)
正の実数全部の集合$\R_+$と通常の乗法・の可換群$(\R_{+},\cdot)$を考えます.
生成される部分群$\langle2,\sqrt{3}\rangle$は2と$\sqrt{3}$とそれらの逆元$\frac{1}{2}$と$\frac{1}{\sqrt{3}}(=\frac{\sqrt{3}}{3})$を自由に演算してできる実数全部の集合なので,
\begin{align*}\langle2,\sqrt{3}\rangle=\set{2^n\sqrt{3}^m}{m,n\in\Z}\end{align*}
となります.つまり,$2^n3^{m’}$, $2^n3^{m’}\sqrt{3}$($m’,n\in\Z$)の形からなる実数全部の集合ですから,
\begin{align*}6,\quad 2\sqrt{3},\quad \frac{1}{2},\quad \frac{3}{4},\quad \frac{\sqrt{3}}{12}\end{align*}
などはいずれも$\langle2,\sqrt{3}\rangle$の元ですね.
具体例3(群$(\mrm{GL}_2(\R),\cdot)$での$\anb{\frac{1}{\sqrt{2}}\sbmat{1&-1\\ 1&1}}$)
一般線形群$(\mathrm{GL}_{2}(\R),\cdot)$を考えます.
$A=\dfrac{1}{\sqrt{2}}\bmat{1&-1\\1&1}$とし,生成される部分群$\anb{A}$を求めましょう.
\begin{align*}A=\bmat{\cos{\frac{\pi}{4}}&-\sin{\frac{\pi}{4}}\\\cos{\frac{\pi}{4}}&\sin{\frac{\pi}{4}}}\end{align*}
は2次列ベクトルに左からかけると原点中心,$\dfrac{\pi}{4}$回転を引き起こす回転行列なので,$A$は8乗して初めて単位行列$I_n$になります.
8乗までは全て異なる行列で,$A^9=A$と$A$に戻るので
\begin{align*}\anb{A}=\set{A^n\in\mathrm{GL}_{2}(\R)}{n=1,2,\dots,8}\end{align*}
となります.これでも何も間違いではありませんが,$A^n$($n=1,2,\dots,8$)を全て成分で表すと
\begin{align*}\anb{A}&=\left\{\frac{1}{\sqrt{2}}\bmat{1&-1\\1&1},\bmat{0&-1\\1&0},\frac{1}{\sqrt{2}}\bmat{-1&-1\\1&-1},\bmat{-1&0\\0&-1},\right.
\\&\qquad\left.\frac{1}{\sqrt{2}}\bmat{-1&1\\-1&-1},\bmat{0&1\\-1&0},\frac{1}{\sqrt{2}}\bmat{1&1\\-1&1},\bmat{1&0\\0&1}\right\}\end{align*}
となりますね.
$A^{-1}=A^7$なので$A^{-1}$も併せて自由に演算しても$A,A^2,\dots,A^7,A^8=I$のいずれかになります.
生成される部分群が可換であるための必要十分条件
群$(G,\cdot)$と空でない部分集合$S\subset G$に対して,次は同値である.
- 生成される部分群$\anb{S}$が可換である.
- 任意の$a,b\in S$が可換である.
つまり,部分集合$S$のどの2元も可換なら$\anb{S}$が可換群になるし,部分集合$S$が可換でない2元をもてば$\anb{S}$が非可換群になるということですね.
[(1)⇒(2)の証明]任意の$g,h\in S$に対して$g,h\in\anb{S}$であり,$\anb{S}$は可換なので$gh=hg$が成り立つ.
[(2)⇒(1)の証明]任意に$g,h\in\anb{S}$をとり,
\begin{align*}g=g_1g_2\dots g_r,\quad h=h_1h_2\dots h_s\end{align*}
と表す.ただし,各$g_i$, $h_j$は$S$の元または$S$の元の逆元である.
ここで,任意の$g,h\in S$に対して,$gh=hg$より
\begin{align*}g^{-1}h=g^{-1}hgg^{-1}=g^{-1}ghg^{-1}=hg^{-1}\end{align*}
なので$g^{-1}$, $h$も可換となり,同様に$g$, $h^{-1}$も可換で$g^{-1}$, $h^{-1}$も可換である.よって,
\begin{align*}gh&=(g_1g_2\dots g_r)(h_1h_2\dots h_s)
\\&=h_1(g_1g_2\dots g_r)h_2\dots h_s
\\&=h_1h_2(g_1g_2\dots g_r)h_3\dots h_s
\\&=\dots=(h_1h_2\dots h_s)(g_1g_2\dots g_r)=hg\end{align*}
が成り立つ.
巡回群の定義・具体例・性質
1つの元から生成される群を巡回群といいます.
群$(G,\cdot)$が巡回群(cyclic group)であるとは,$G=\anb{g}$となる$g\in G$が存在することをいう.
具体例1(群$(\Z,+)$は巡回群)
$\Z$と通常の加法+の可換群$(\Z,+)$について,生成される部分群$\anb{1}$は1と−1(1の逆元)を自由に演算してできる整数全部の集合なので,
\begin{align*}\anb{1}=\set{n\cdot1}{n\in\Z}=\Z\end{align*}
となります.すなわち,$\Z$は1つの元により生成されるので,群$(\Z,+)$は巡回群です.
$\Z$全体を生成する元が1つでもあれば巡回群なので,具体的に$\Z$を生成する1をとってきたわけですね.
具体例2(群$(\Z_6,+)$は巡回群)
集合$\Z_6=\{\overline{0},\overline{1},\overline{2},\overline{3},\overline{4},\overline{5}\}$上の演算+を
\begin{align*}\overline{m}+\overline{n}=\overline{(\text{$m+n$を6で割った余り})}\end{align*}
と定めます.例えば
\begin{align*}&\overline{1}+\overline{1}=\overline{2},\quad
\overline{4}+\overline{5}=\overline{3},\quad
\overline{2}+\overline{4}=\overline{0}\end{align*}
といった具合に,6に達すると0に戻る演算がいまの演算+ですね.
合同式を知っていれば$\operatorname{mod}\ 6$で計算していると考えれば分かりやすいでしょう.
このとき$(\Z,+)$が(可換)群になっていることは,以下の記事で証明しているので参照してください.
$\overline{1}\in\Z_6$を繰り返し演算すれば$\overline{1},\overline{2},\overline{3},\overline{4},\overline{5},\overline{0}$が順次できあがるので,$\langle\overline{1}\rangle=\Z_6$となります.
すなわち,$\Z_6$は1つの元により生成されるので,群$(\Z_6,+)$は巡回群です.
一般に集合$\Z_n=\{\overline{0},\overline{1},\dots,\overline{n}\}$と,同様に$n$で割った余りを考える和+の組$(\Z_n,+)$は巡回群となります.
具体例3(群$(\Q,+)$は巡回群でない)
$\Q$と通常の加法+の可換群$(\Q,+)$は巡回群でないことを示しましょう.
任意の$r\in\Q$に対して,$\R$における$\Q$の稠密性より0と$r$の間にも有理数が存在します.一方,
\begin{align*}\anb{r}=\set{nr}{n\in\Z}\end{align*}
なので,$\anb{r}$は0と$r$の間の有理数を元に持たないので$\anb{r}\subsetneq\Q$です.
$r$は任意だったので$\Q$の生成元となる$r\in\Q$は存在せず,可換群$(\Q,+)$は巡回群ではありません.
補題の証明
最後に,生成される部分群が群となるという最初の補題を証明しましょう.
(再掲)群$(G,\cdot)$と空でない部分集合$S\subset G$を考え,集合$S$の元とその逆元を自由に演算してできる元全部の集合を$H$とする.すなわち,複号任意で
\begin{align*}H:=\set{g_1^{\pm1}g_2^{\pm1}\dots g_n^{\pm1}}{\begin{gathered}g_1,g_2,\dots,g_n\in S\end{gathered}}\end{align*}
とする.このとき,$(H,\cdot)$は$(G,\cdot)$の部分群となる.
- $G$の単位元が$H$に属すること
- 演算・で$H$が閉じていること
- 逆元をとる操作で$H$が閉じていること
を示せばよい.
$G$の単位元が$H$に属すること
$e_G$を$G$の単位元とする.
任意の$g\in S$に対して,$e_G=gg^{-1}\in\anb{S}$が成り立つ.
演算・で$H$が閉じていること
任意に$g,h\in\anb{S}$をとり,
\begin{align*}g={g_1}^{\pm1}{g_2}^{\pm1}\dots{g_r}^{\pm1},\quad
h={h_1}^{\pm1}{h_2}^{\pm1}\dots{h_s}^{\pm1}\end{align*}
と表す.ただし,$g_i,h_j\in S$($i=1,2,\dots,r$, $j=1,2,\dots,s$)である.よって,
\begin{align*}gh=(g_1^{\pm1}g_2^{\pm1}\dots g_r^{\pm1})(h_1^{\pm1}h_2^{\pm1}\dots h_s^{\pm1})\end{align*}
も$S$の元または$S$の元の逆元を演算してできる元だから$S$に属する.
逆元をとる操作で$H$が閉じていること
任意に$g,h\in\anb{S}$をとり,
\begin{align*}g={g_1}^{\pm1}{g_2}^{\pm1}\dots{g_r}^{\pm1}\end{align*}
と表す.ただし,$g_i\in S$($i=1,2,\dots,r$)である.よって,
\begin{align*}g^{-1}={g_r}^{\mp1}\dots{g_2}^{\mp1}{g_1}^{\mp1}\end{align*}
も$S$の元または$S$の元の逆元を演算してできる元だから$S$に属する.

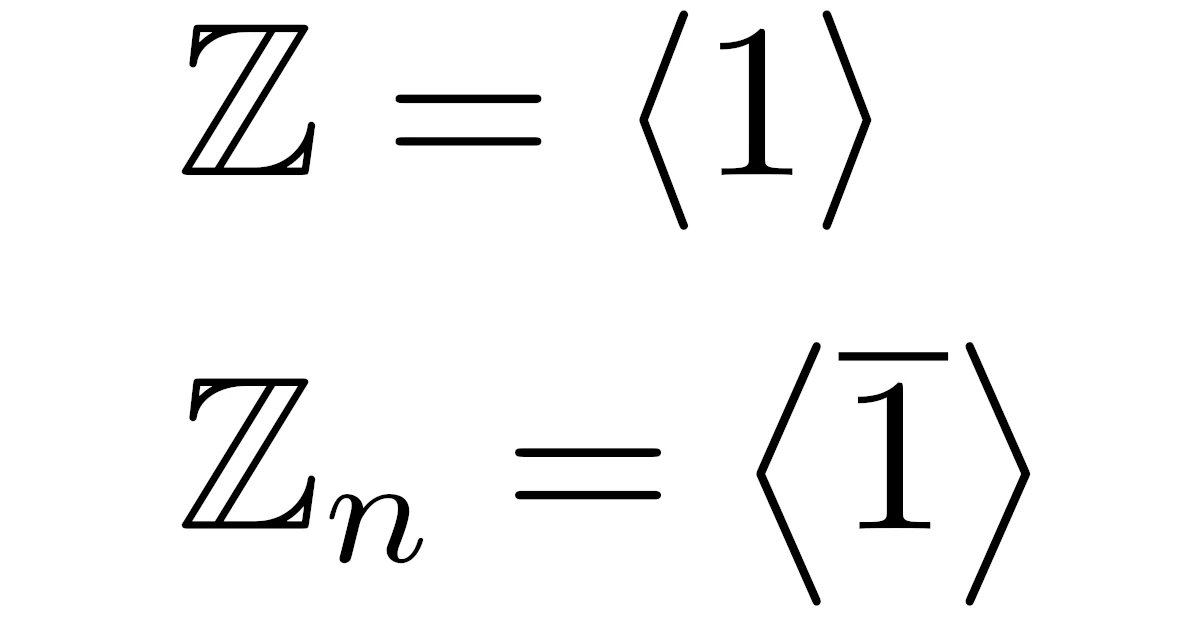
コメント