有理数は実数上に密に存在しており，この性質を（実数における）有理数の稠密性といいます（稠のつくりが「周」でないことに注意）．
もう少しきちんというなら「どんなに近い２つの実数の間にも有理数が存在する」ということになります．
この有理数の稠密性を厳密に証明するには，アルキメデスの性質と呼ばれる実数の性質を用いることになります．
アルキメデスの性質はアルキメデスの原理と呼ばれることもありますが，物理の浮力に関するアルキメデスの原理とは全くの別物です．
この記事では
- 有理数の集合の稠密性
- アルキメデスの性質（アルキメデスの原理）
- 無理数の集合の稠密性
を順に説明します．
「微分積分学の基本」の一連の記事
微分積分学の参考文献
以下は微分積分学に関するオススメの教科書です．
微分積分学（笠原晧司 著）
数学科など理論系の学生向けの微分積分学の入門書です．基本的な例から発展的な例まで扱われており，バランスの良い教科書です．
有理数の集合の稠密性
実数の集合における次の性質を有理数の稠密性といいます．
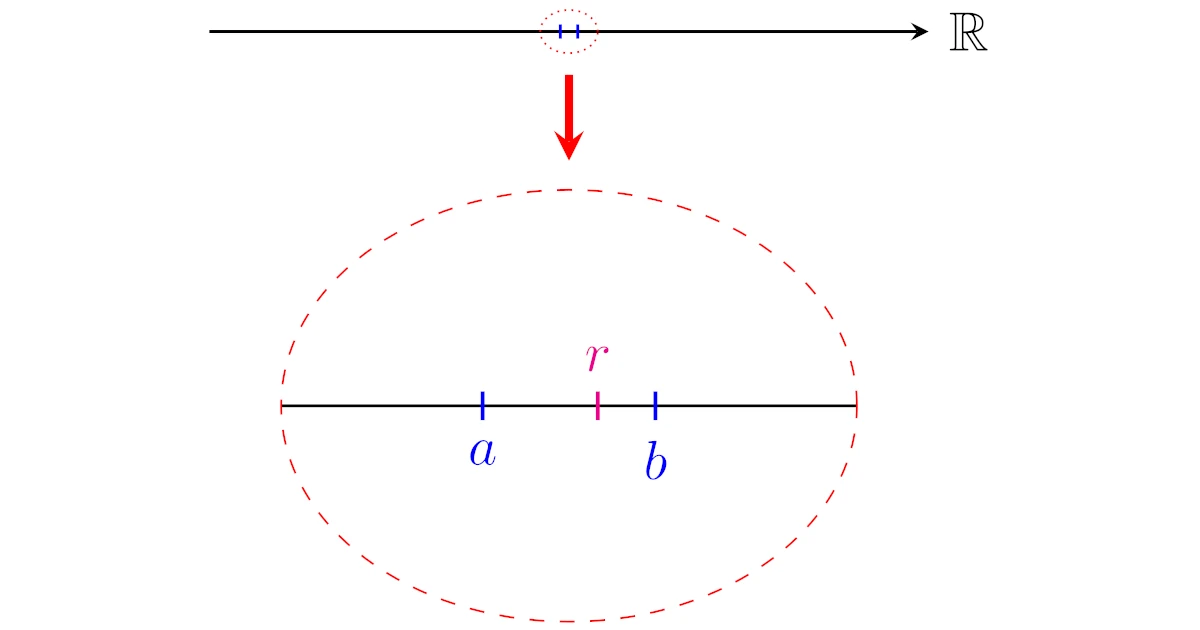
［有理数の稠密性］$a<b$を満たす任意の$a,b\in\R$に対して，$a<r<b$なる有理数$r$が存在する．
つまり，どんなに実数$a,b$が近くてもその間に有理数が存在するというわけですね．
極限$\lim\limits_{n\to\infty}\dfrac{1}{n}=0$より，$\dfrac{1}{N}<b-a$を満たす正の整数$N$が存在する．
この$N$に対して$\dfrac{k}{N}\le a<b\le\dfrac{k+1}{N}$なる整数$k$は存在しない．
よって，$a<\dfrac{K}{N}<b$を満たす整数$K$が存在する．
$\dfrac{K}{N}$は有理数だから，$a<r<b$を満たす有理数$r$が存在する．
この証明で何も間違っていませんが，ひとつ気がかりなことがあります．それは「本当に$\lim\limits_{n\to\infty}\dfrac{1}{n}=0$が成り立つのか？」ということです．
実は高校数学から使ってきたこの収束は高校数学の範囲では証明していません．
その理由はこの収束をきちんと証明するために実数の性質であるアルキメデスの性質を用いる必要があるためで，このアルキメデスの性質は高校範囲外だからです．
よって，収束$\lim\limits_{n\to\infty}\dfrac{1}{n}=0$を示すことができれば，有理数の集合の稠密性がきちんと証明できたことになりますね．
アルキメデスの性質（アルキメデスの原理）
ここで実数の性質であるアルキメデスの性質を紹介します．そのあと極限$\lim\limits_{n\to\infty}\dfrac{1}{n}=0$を証明しましょう．
アルキメデスの性質と証明
次の定理をアルキメデスの性質（またはアルキメデスの原理）と言います．
［アルキメデスの性質］任意の正の実数$p,q$に対して，ある正の整数$N$が存在して$p<Nq$が成り立つ．
どんなに$p$が$q$より大きくても，$q$の２倍$2q$，３倍$3q$，……と$q$にかける正の整数を大きくしていくと，いつかは$p$より$nq$ ($n\in\N$)の方が大きくなるというわけですね．
直感的にはそう難しくないと思いますが，証明には実数の連続性公理（上限性質）を本質的に用います．
背理法により示す．すなわち，ある$q\in\R$が存在して，任意の$n\in\N$に対して$p\ge nq$が成り立つと仮定して矛盾を導く．
背理法の仮定から$\R$の部分集合$\set{nq\in\R}{n\in\N}$は$p$を上界にもつから，実数の連続性公理より
が存在する．
このとき，上限$\sup$の性質から任意の$\epsilon>0$に対して$\alpha-\epsilon<mq$を満たす$m\in\N$が存在する．$\epsilon$は任意なので$\epsilon=q$としてもよく，このとき
が成り立つ．$m+1\in\N$より
なので，$\alpha$より大きい$\set{nq\in\R}{n\in\N}$の元が存在することになり，$\alpha$が上限であることに矛盾する．
よって，仮定は誤りなので定理が成り立つ．
収束$\lim\limits_{n\to\infty}\dfrac{1}{n}=0$の証明
いまのアルキメデスの性質で$p=1$, $q=\epsilon$とすると，収束$\lim\limits_{n\to\infty}\dfrac{1}{n}=0$が得られます．
極限$\lim\limits_{n\to\infty}\dfrac{1}{n}=0$が成り立つ．
任意に$\epsilon>0$をとる．アルキメデスの原理より，ある$N\in\N$が存在して
が成り立つ．よって，$n>N$なら
となって，$\epsilon\text{-}N$論法による収束の定義から$\lim\limits_{n\to\infty}\dfrac{1}{n}=0$を得る．
これで有理数の集合の稠密性もきちんと証明されたことになりますね．
無理数の集合の稠密性
実は有理数の集合だけではなく，無理数の集合にも稠密性があります．
[無理数の集合の稠密性] $a<b$を満たす任意の$a,b\in\R$に対して，$a<\gamma<b$なる無理数$\gamma$が存在する．
証明は有理数の場合とほとんど同じです．
$\lim\limits_{n\to\infty}\dfrac{1}{n}=0$より，
を満たす正の整数$N$が存在する．
この$N$に対して$\dfrac{k}{\sqrt{2}N}\le a<b\le\dfrac{k+1}{\sqrt{2}N}$なる整数$k$は存在しないから，$a<\dfrac{K}{\sqrt{2}N}<b$を満たす整数$K$が存在する．
$\dfrac{K}{\sqrt{2}N}$は無理数だから，$a<\gamma<b$を満たす無理数$\gamma$が存在する．
有理数も無理数も実数上に密に存在しているなら，有理数と無理数ではどちらの方が多いのか気になるかも知れません．
数学には集合の元の「多さ」の指標に濃度（Cardinality）というものがあり，
- 有理数全部の集合$\Q$の濃度
- 無理数全部の集合$\R\setminus\Q$の濃度
を比較すると，無理数の方が多いことが証明できます．このことについて詳しくは以下の記事を参照してください．
コメント