例えば，確率論・ルベーグ積分論はどちらも測度論という分野に属します．
確率と積分は全く違うように感じるかも知れませんが，測度論は「集合の元の量を測る」という考え方がベースにある分野で
- 「集合の元の量」を頻度として扱うのが確率論
- 「集合の元の量」を長さとして扱うのがルベーグ積分論
とどちらも「集合の元の量を測る」という観点では同じわけですね．
さて，測度論における基本的な空間として可測空間・測度空間がありますが，最初はこれらのイメージが掴みにくく困惑してしまうことも少なくありません．
そこでこの記事では，直感的な考え方をたどりながら
- 集合族と冪集合
- 可測空間の定義と具体例
- 測度空間の定義と具体例
を順に説明します．
参考文献
確率論
[舟木直久 著/朝倉書店]
本書は確率論の入門書で，全体を通して丁寧に書かれています．
第1章では確率論の概説がなされており，例えば「大数の弱法則」「大数の強法則」にまで平易な説明で触れられているのが嬉しいです．
ただし，本書の「まえがき」に書かれているように，第２章から第５章は大学３年〜４年相当の確率論の内容となっているので，第２章以降を読むにはそれなりの基礎が必要となります．
第６章，第７章では代表的な確立過程である「マルチンゲール」「マルコフ過程」が解説されています．
本書は全体を通して「なぜその概念を学ぶ必要があるのか」という動機付けが大切にされており，新しい概念を前向きに理解しやすい点が優れている好著となっています．
集合族と冪集合
可測空間・測度空間を考えるには集合族というものが必要です．
集合族の定義
高校数学で集合といえば，例えば
- １から５までの整数の集合$\{1,2,3,4,5\}$
- 実数（数直線）上の3以上7未満の区間
のように，「数」をパッケージしたもののことを指すことがほとんどでしたが，実は数でないものをパッケージした集合もあります．
大学以降の数学では，例えば
- 区間$[0,1]$で定義された実数値関数の集合
- 集合$\{1,2,3\}$の部分集合全部の集合
といった集合も考えるようになります．
さて，可測空間・測度空間において必要になる集合族とは次のように定義されます．
集合の集合を集合族（family of sets）という．
PCでは「フォルダの中にフォルダを保存する」ということをよくしますが，フォルダを集合だと思うとこれはまさに集合族と同じことですね．
例えば，上で挙げた「集合$\{1,2,3\}$の部分集合全部の族」は
と表せるわけですが，これは集合をパッケージしているので集合族ということになりますね．
冪集合の定義
集合族の中でも冪集合と呼ばれる集合族はよく現れるので定義しておきましょう．
部分集合全部の集合$X$の部分集合全部の族を$X$の冪集合（power set）といい，$\mathcal{P}(X)$や$2^X$などと表す．
例えば，上で挙げた「集合$\{1,2,3\}$の部分集合全部の族」は$\{1,2,3\}$の冪集合ということができ，
というわけですね．
冪集合を$\mathcal{P}(X)$と表すのは冪集合の英語“power set”の頭文字に由来し，$2^X$と表すのは$X$の全ての部分集合が「$X$の各元で属するか否かの２通りを選んでできる集合」ということに由来します．
可測空間の定義と具体例
集合族が準備できたので，可測空間について解説していきます．
定義
先に可測空間を定義して，そのあと直感的な考え方を説明します．
集合$X$と$X$の部分集合の族$\mathcal{F}$が３条件
- $X\in\mathcal{F}$
- $A\in\mathcal{F}\Ra A^c\in\mathcal{F}$
- $A_1,A_2,\dots\in\mathcal{F}\Ra \bigcup\limits_{n=1}^{\infty}A_n\in\mathcal{F}$
を満たすとき，組$(X,\mathcal{F})$を可測空間（measurable space）という．また，$\mathcal{F}$を$X$の完全加法族（completely additive class）という．
完全加法族は$\sigma$-加法族など他の呼び方もあります．
初見では条件(1)-(3)のイメージは掴みづらいですが，直感的には「$X$の部分集合のうち観測できるものを集めたのが$\mathcal{F}$」と考えることができます．
つまり，$A\in\mathcal{F}$を「$A$が観測できる」と読みかえると，条件(1)-(3)は
- 何かが起こったことは観測できる（$X$全体は観測できる）
- 何かが起こっても$A$を観測しなかったら，それは「$A$でない」と観測できる（$A$が観測できるなら，$A^c$（$A$でないもの）も観測できる）
- 観測できるものを併せたものも観測できる（$A_1,A_2,\dots$が観測できるなら，$A_1\cup A_2\cup\dots$も観測できる）
となり，確かに「$\mathcal{F}$に属する集合を観測できる」という気持ちが見てとれますね．
よって，$\mathcal{F}$を考えることは観測できる状況を考えることになるのですが，このことを具体例から考えてみましょう．
具体例１（カードの選択）
表に$1,2,3$が書かれたカード$\fbox{1}$, $\fbox{2}$, $\fbox{3}$が１枚ずつある．
裏向きに置いたこれら３枚のカードから１枚を選ぶとき，選ばれる数字について可測空間を設定せよ．
最初はどう答えればよいか難しい問題ですが，
- 実際に起こるものの集合を$X$
- 観測できる$X$の部分集合族を$\mathcal{F}$
として設定する問題です．
解答例を書いて，そのあと考え方を説明します．
選ばれる数字は$1,2,3$なので$X=\{1,2,3\}$とする．
また，どの数字も区別して観測できるので，$\mathcal{F}$を$X$の冪集合とする：
このとき，組$(X,\mathcal{F})$は可測空間であり，問題のカード選択の状況を表す．
$\mathcal{F}$の直感的な考え方
いまカードはどれも区別できるので，
- 「$\fbox{1}$を選んだ」
- 「$\fbox{2}$を選んだ」
- 「$\fbox{2}$または$\fbox{3}$を選んだ」
などの状況を観測できます．これらはそれぞれ
- $\{1\}\in\mathcal{F}$
- $\{2\}\in\mathcal{F}$
- $\{2,3\}\in\mathcal{F}$
に対応するわけですね．どんなカードの選び方も観測できるので，$\mathcal{F}$は$X$の冪集合とできるわけですね．
$(X,\mathcal{F})$が可測空間であること
また，可測空間の定義の３条件を満たしていることも確認できますね．つまり，
- $X\in\mathcal{F}$は$\mathcal{F}$の定義から成り立ちます．
- 例えば$\{1\}\in\mathcal{F}$なので$\{1\}^c=\{2,3\}\in\mathcal{F}$でなければなりませんが，確かに成り立っています．
$\mathcal{F}=\mathcal{P}(X)$なので，$\mathcal{F}$に属する$\{1\}$以外の集合についても補集合は$\mathcal{F}$に属しますね． - 例えば$\{1\},\{2\}\in\mathcal{F}$なので$\{1\}\cup\{2\}=\{1,2\}\in\mathcal{F}$でなければなりませんが，確かに成り立っています．
$\mathcal{F}=\mathcal{P}(X)$なので，$\mathcal{F}$に属する$\{1\},\{2\}$をとる以外でも和集合は$\mathcal{F}$に属しますね．
よって，確かに$(X,\mathcal{F})$は可測空間・$\mathcal{F}$は完全加法族と分かりますね．
具体例２（６面サイコロ）
普通の６面サイコロの出目について可測空間を設定せよ．
考え方としては具体例１と同じですね．
出目は$1,2,3,4,5,6$なので$X=\{1,2,3,4,5,6\}$とする．
また，どの出目も区別して観測できるので，$\mathcal{F}=\mathcal{P}(X)$とする．
このとき，組$(X,\mathcal{F})$は可測空間であり，問題の６面サイコロの状況を表す．
具体例１のカードが６枚に増えたのと本質的には全く同じですね．
$\mathcal{F}=\mathcal{P}(X)$であることから，具体例１と同様に$(X,\mathcal{F})$は可測空間・$\mathcal{F}$は完全加法族と分かりますね．
一般に次が成り立つことが分かりますね．
集合$X$と冪集合$\mathcal{F}=\mathcal{P}(X)$に対して，組$(X,\mathcal{F})$は可測空間である．
具体例３（汚れたカードの選択１）
具体例１と具体例２では$\mathcal{F}=\mathcal{P}(X)$としましたが，そうでない例も見ておきましょう．
表に$1,2,3$が書かれたカード$\fbox{1}$, $\fbox{2}$, $\fbox{3}$が１枚ずつあったが，カードを汚してしまい全てのカードの区別がつかなくなってしまった．
このとき，裏向きに置いたこれら３枚のカードから１枚を選ぶとき，選ばれる数字について可測空間を設定せよ．
カードは汚れていますが，カードを選ぶと実際には$\fbox{1}$, $\fbox{2}$, $\fbox{3}$のどれかが選ばれてはいるはずなので，$X$は具体例１と同じです．
しかし，「$\fbox{1}$を選んだ」「$\fbox{2}$または$\fbox{3}$を選んだ」などは観測できませんから，$\mathcal{F}$が変わり次のようになります．
選ばれる数字は$1,2,3$なので$X=\{1,2,3\}$とする．
また，どのカードも区別できないので，$\mathcal{F}=\{\emptyset,X\}$とする．
このとき，組$(X,\mathcal{F})$は可測空間であり，問題のカード選択の状況を表す．
どのカードも区別できないということは，「何かが起こった」「何も起こっていない」ことしか観測できないということですから，$\mathcal{F}=\{\emptyset,X\}$ということですね．
この場合も$(X,\mathcal{F})$が可測空間になることは，３条件をひとつずつ確かめれば分かりますね．
具体例１・具体例２とは対照的に，この具体例３から一般に次が成り立つことが分かりますね．
集合$X$と集合族$\mathcal{F}=\{\emptyset,X\}$に対して，組$(X,\mathcal{F})$は可測空間である．
具体例４（汚れたカードの選択２）
$\mathcal{F}=\mathcal{P}(X)$でも$\mathcal{F}=\{\emptyset,X\}$でもない例も見ておきましょう．
表に$1,2,3$が書かれたカード$\fbox{1}$, $\fbox{2}$, $\fbox{3}$が１枚ずつあったが，カードを汚してしまい$\fbox{1}$と$\fbox{2}$の区別がつかなくなってしまった．
このとき，裏向きに置いたこれら３枚のカードから１枚を選ぶとき，選ばれる数字について可測空間を設定せよ．
今回は$\fbox{1}$, $\fbox{2}$の区別はつきませんが，$\fbox{3}$は区別できます．
そのため，例えば「$\fbox{1}$か$\fbox{2}$を選んだ」「$\fbox{3}$を選んだ」は観測できるので
となるように，一方「$\fbox{1}$を選んだ」「$\fbox{2}$を選んだ」は観測できないので
となるように$\mathcal{F}$を設定したいですね．
選ばれる数字は$1,2,3$なので$X=\{1,2,3\}$とする．
また，$\fbox{1}$と$\fbox{2}$の区別がつかないだけなので，$\mathcal{F}=\{\emptyset,\{1,2\},\{3\},X\}$とする．
このとき，組$(X,\mathcal{F})$は可測空間であり，問題のカード選択の状況を表す．
また，今回の組$(X,\mathcal{F})$が可測空間であることも，３条件をひとつずつ確かめれば分かります．
測度空間の定義と具体例
測度空間は「観測できる集合の元の量を測る」ことができる空間です．
定義
可測空間の「観測できる集合の元の量」を測れる空間が測度空間です．
可測空間$(X,\mathcal{F})$と関数$\mu:\mathcal{F}\to\R_{\ge0}$が２条件
- $\mu(\emptyset)=0$
- $A_1,A_2,\dots\in\mathcal{F}$が互いに素（$i\neq j$なら$A_i\cap A_j=\emptyset$）なら，$\mu\bra{\bigcup_{n=1}^{\infty}A_n}=\sum_{n=1}^{\infty}\mu(A_n)$
を満たすとき，組$(X,\mathcal{F},\mu)$を測度空間（measure space）という．また，$\mu$を$(X,\mathcal{F})$上の測度（measure）という．
(2)の性質を測度の完全加法性といいます．直感的には測度$\mu$は「観測できる集合の元の量」を測る関数になっています．
このことから，条件(1), (2)は次のように言えますね：
- 「空集合$\emptyset$の元の量」は０である
- 被りのない集合たちについて，「和集合の元の量」と「それぞれの集合の元の量」の総和は等しい
測度$\mu$を変えることは「観測できる集合の元の量」の「重み」を変えることになるのですが，このことを具体例から考えてみましょう．
具体例１（カードの選択）
表に$1,2,3$が書かれたカード$\fbox{1}$, $\fbox{2}$, $\fbox{3}$が１枚ずつある．
裏向きに置いたこれら３枚のカードから無作為に１枚を選ぶとき，選ばれる数字の頻度について可測空間を設定せよ．
カードの選択の状況は上で考えた可測空間の具体例１と同じものを考えます．
あとは測度$\mu$をどのように定めるかですが，今はランダムにカードを選ぶので，例えば
- $\fbox{1}$を選ぶ頻度は$\dfrac{1}{3}$
- $\fbox{2}$を選ぶ頻度は$\dfrac{1}{3}$
- $\fbox{1}$または$\fbox{3}$を選ぶ頻度は$\dfrac{2}{3}$
となるように$\mu$を設定したいですね．
$X=\{1,2,3\}$, $\mathcal{F}=\mathcal{P}(X)$とすると，組$(X,\mathcal{F})$は可測空間である．
また，関数$\mu:\mathcal{F}\to\R_{\ge0}$を
- $\mu(\emptyset)=0$
- $\mu(\{1\})=\mu(\{2\})=\mu(\{3\})=\dfrac{1}{3}$
- $\mu(\{1,2\})=\mu(\{1,3\})=\mu(\{2,3\})=\dfrac{2}{3}$
- $\mu(X)=\dfrac{3}{3}(=1)$
と定めると，組$(X,\mathcal{F},\mu)$は測度空間であり，問題のカード選択の状況を表す．
$\mu$の定義の１つ目の定義は測度空間の条件(1)そのものであり，集合の元の個数$r$によって$\mu$が返す値が決まるので測度空間の条件(2)を満たすことも分かります．
よって，組$(X,\mathcal{F},\mu)$は測度空間，$\mu$は$(X,\mathcal{F})$上の測度と分かるわけですね．
具体例２（いびつな６面サイコロ）
１の目のみ出やすい６面サイコロの出目の頻度について測度空間を設定せよ．
出目と観測できる事象は普通の６面サイコロなので，可測空間$(X,\mathcal{F})$は可測空間の具体例２と同じものを考えます．
測度$\mu$は１の目が出やすいように定めるので，集合に１が属しているか否かで「重み」が異なるように$\mu$定めます．
$X=\{1,2,3,4,5,6\}$, $\mathcal{F}=\mathcal{P}(X)$とすると，組$(X,\mathcal{F})$は可測空間である．
また，関数$\mu:\mathcal{F}\to\R_{\ge0}$を
- $\mu(\emptyset)=0$
- $\mu(\{1\})=\dfrac{5}{10}\bra{=\dfrac{1}{2}}$
- 異なる$k_1,\dots,k_r\in\{2,3,4,5,6\}$に対して$\mu(\{k_1,\dots,k_r\})=\dfrac{r}{10}$
- 異なる$k_1,\dots,k_r\in\{2,3,4,5,6\}$に対して$\mu(\{1,k_1,\dots,k_r\})=\dfrac{5+r}{10}$
と定めると，組$(X,\mathcal{F},\mu)$は測度空間であり，１の目が全体の半分の頻度で出るサイコロの状況を表す．
ここで定めた関数$\mu$は，例えば
- $\mu(\{3,5,6\})=\dfrac{3}{10}$
- $\mu(\{1,3\})=\dfrac{5+1}{10}=\dfrac{6}{10}=\dfrac{3}{5}$
ということで，この場合も測度空間の２条件を満たすことが分かります．
確率空間の定義
測度空間の中でも特別なものに確率空間と呼ばれる空間があります．
測度空間$(\Omega,\mathcal{F},\mu)$について，測度$\mu$が
を満たすとき，$(\Omega,\mathcal{F},\mu)$を確率空間（probability space）といい，$\mu$を確率測度または単に確率という．
慣習的に確率空間の集合は$\Omega$で表し，確率測度は$\mathbb{P}$や単に$P$と表すことが多いです．
つまり，「$\Omega$全体の量を測ると$1$」になっている測度空間を確率空間というわけですね．
例えば，上で見た具体例１の測度$\mu$は
を満たし，具体例２の測度$\mu$も
を満たすので，どちらの測度空間も確率空間で$\mu$は確率測度になっていたわけですね．
注意
測度空間$(X,\mathcal{F},\mu)$について，測度$\mu$が測れるのは$\mathcal{F}$に属する集合（観測できる集合）のみであることに注意しましょう．
そのため，測度$\mu$に代入できるのは集合なので，例えば
- 集合$\{1\}$の測度は$\mu(1)$ではなく$\mu(\{1\})$が正しい
- 集合$\{2,3\}$の測度は$\mu(2,3)$ではなく$\mu(\{2,3\})$が正しい
ということも意識したいポイントです．
また，測度空間の条件(1)では$\mu(\emptyset)$を考えていますが，これは可測空間の条件(1)と条件(2)と併せると$\emptyset=\Omega^c\in\mathcal{F}$が成り立つので，$\mu(\emptyset)$を考えることに問題はありませんね．
さらに，測度空間の条件(2)では$\mu\bra{\bigcup\limits_{n=1}^{\infty}A_n}$を考えていますが，これは可測空間の条件(3)で
を保証しているので，こちらも$\mu\bra{\bigcup\limits_{n=1}^{\infty}A_n}$を考えることに問題はありませんね．
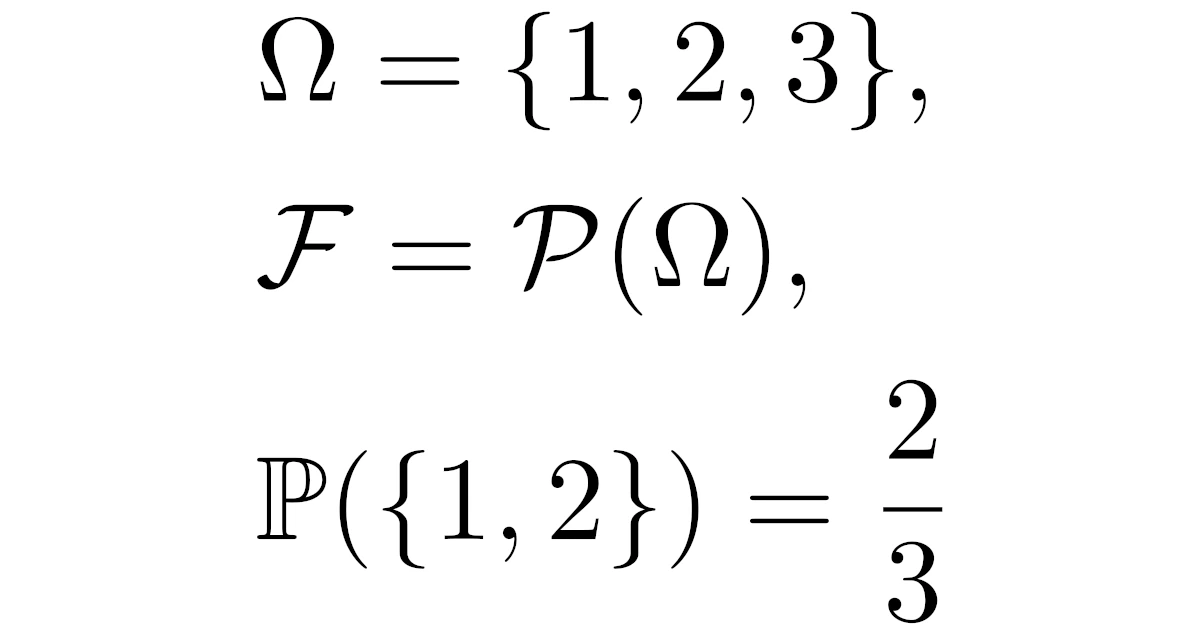
コメント