ルベーグ積分や確率論をはじめとする測度論では,集合の列$\{A_n\}$を考えることがよくあります.
このとき,集合$A_n$の測度の極限$n\to\infty$に関して述べた測度の単調収束定理が重要な役割を果たすことがよくあります.
測度の単調収束定理は
- 単調増大列$A_1\subset A_2\subset A_3\subset\dots$の場合
- 単調減少列$A_1\supset A_2\supset A_3\supset\dots$の場合
の2通りがあります.
この記事では
- 測度の単調収束定理
- 単調減少列の場合の補足
- 測度の単調収束定理の応用例
を順に説明します.
測度の単調収束定理
次の定理が測度の単調収束定理です.
単調増大列の場合
$(X,\mathcal{F},\mu)$を測度空間とする.このとき,$A_1,A_2,\dots\in\mathcal{F}$が$A_1\subset A_2\subset A_3\subset\dots$を満たすなら,
\begin{align*}\mu{\bra{\bigcup_{n=1}^{\infty}A_n}}=\lim_{n\to\infty}\mu(A_n)\end{align*}
が成り立つ.
ざっくり言えば,集合がどんどん大きくなるなら,全ての集合の和集合の測度は測度の極限に一致するということですね.
このことは$\bigcup_{n=1}^{N}A_n=A_{N}$であることから見てとれますね.
集合$B_1,B_2,\dots\in\mathcal{F}$を
\begin{align*}B_1:=A_1,\quad
B_n:=A_{n}\setminus A_{n-1}\quad (n=2,3,\dots)\end{align*}
により定めると,$A_1\subset A_2\subset\dots$より$B_1,B_2,\dots$は互いに素である.
$\bigcup_{n=1}^{\infty}A_n=\bigcup_{n=1}^{\infty}B_n$であることに注意すると,$\mu$の完全加法性と併せて
\begin{align*}\mu{\bra{\bigcup_{n=1}^{\infty}A_n}}
=&\mu{\bra{\bigcup_{n=1}^{\infty}B_n}}
=\sum_{n=1}^{\infty}\mu{(B_n)}
\\=&\lim_{N\to\infty}\sum_{n=1}^{N}\mu{(B_n)}
=\lim_{N\to\infty}\mu{\bra{\bigcup_{n=1}^{N}B_n}}
\\=&\lim_{N\to\infty}\mu{(A_{N+1})}
=\lim_{n\to\infty}\mu(A_n)\end{align*}
を得る.
単調減少列の場合
$(X,\mathcal{F},\mu)$を測度空間とする.このとき,$A_1,A_2,\dots\in\mathcal{F}$が$A_1\supset A_2\supset A_3\supset\dots$を満たし,ある$N\in\N$が存在して$\mu(A_N)<\infty$を満たすなら,
\begin{align*}\mu{\bra{\bigcap\limits_{n=1}^{\infty}A_n}}=\lim\limits_{n\to\infty}\mu(A_n)\end{align*}
が成り立つ.
ざっくり言えば,集合がどんどん小さくなり,どこかから有限測度になるなら,全ての集合の共通集合の測度は測度の極限に一致するということですね.
このことは$\bigcap_{n=1}^{N}A_n=A_{N}$であることから見てとれますね.
集合$B_1,B_2,\dots\in\mathcal{F}$を
\begin{align*}B_n:=A_{n}\setminus A_{n+1}\quad (n=1,2,\dots)\end{align*}
により定めると,$A_1\supset A_2\supset\dots$より$B_1,B_2,\dots$は互いに素である.
$\bigcap_{n=1}^{\infty}A_n\subset A_N$なので,測度の単調性より
\begin{align*}\mu{\bra{\bigcap_{n=1}^{\infty}A_n}}\le \mu(A_N)<\infty\end{align*}
だから,
\begin{align*}\mu(A_N)-\mu{\bra{\bigcap_{n=1}^{\infty}A_n}}
=\mu\bra{A_N\setminus\bra{\bigcap_{n=1}^{\infty}A_n}}\end{align*}
が定義できる.ここで,$A_1\supset A_2\supset\dots$に注意すると,
\begin{align*}A_N\setminus\bra{\bigcap_{n=1}^{\infty}A_n}
&=A_N\cap\bra{\bigcap_{n=1}^{\infty}A_n}^c
=A_N\cap\bra{\bigcup_{n=1}^{\infty}{A_n}^c}
\\&=\bigcup_{n=1}^{\infty}(A_N\cap{A_n}^c)
=\bigcup_{n=1}^{\infty}(A_N\setminus A_n)
\\&=\bigcup_{n=N}^{\infty}(A_N\setminus A_n)
=\bigcup_{n=N}^{\infty}B_n\end{align*}
となる.よって,$\mu$の完全加法性と併せて
\begin{align*}\mu(A_N)-\mu{\bra{\bigcap_{n=1}^{\infty}A_n}}
&=\mu\bra{\bigcup_{n=N}^{\infty}B_n}
=\sum_{n=N}^{\infty}\mu(B_n)
\\&=\sum_{n=N}^{\infty}(\mu(A_n)-\mu(A_{n+1}))
\\&=\mu(A_N)-\lim_{n\to\infty}\mu(A_{n})\end{align*}
が成り立つ.よって,整理して
\begin{align*}m{\bra{\bigcap\limits_{n=1}^{\infty}A_n}}=\lim\limits_{n\to\infty}m(A_n)\end{align*}
を得る.
単調減少列の場合の補足
単調減少列の場合の仮定「$N\in\N$が存在して$\mu(A_N)<\infty$」は必要です.つまり,この仮定がないと反例が存在します.
$(X,\mathcal{F},\mu)$を測度空間とする.このとき,
- $A_1\supset A_2\supset A_3\supset\dots$
- $\mu{\bra{\bigcap\limits_{n=1}^{\infty}A_n}}\neq\lim\limits_{n\to\infty}\mu(A_n)$
を同時に満たす$A_1,A_2,\dots\in\mathcal{F}$を構成せよ.
ルベーグ測度空間において,$A_n:=[n,\infty)$とすると
\begin{align*}[1,\infty)\subset[2,\infty)\subset[3,\infty)\subset\dots\end{align*}
なので,$\{A_n\}$は単調減少列である.
[1]任意の$n$に対して$\mu(A_n)=\infty$なので,
\begin{align*}\lim\limits_{n\to\infty}\mu(A_n)=\infty\end{align*}
が成り立つ.
[2]任意の$x\in\R$に対して,ある$N\in\N$が存在して$x<N$となるから$x\notin A_N$である.
よって,共通部分はすべての集合に属する元全部の集合なので,$\bigcap\limits_{n=1}^{\infty}A_n=\emptyset$が従う.よって,
\begin{align*}\mu{\bra{\bigcap\limits_{n=1}^{\infty}A_n}}=\mu(\emptyset)=0\end{align*}
が成り立つ.
[1]と[2]より$\mu{\bra{\bigcap\limits_{n=1}^{\infty}A_n}}\neq\lim\limits_{n\to\infty}\mu(A_n)$が成り立つ.
確率空間など有限測度空間($\mu(X)<\infty$)なら,もとより$\mu(A_n)<\infty$なので仮定「$N\in\N$が存在して$\mu(A_N)<\infty$」は不要ですね.
測度の単調収束定理の応用例
測度の単調収束定理を応用すると次の事実が証明できます.次の事実はよく用いるので当たり前にしておきたいところです.
$(X,\mathcal{F},\mu)$を測度空間とする.$X$上の可測関数$f:X\to\overline{\R}$に対して,次が成り立つ.
- $\lim\limits_{n\to\infty}\mu{\bra{\set{x\in X}{|f(x)|\ge\frac{1}{n}}}}=\mu{\bra{\set{x\in X}{f(x)\neq0}}}$
- $f$が$X$上可積分なら,$\lim\limits_{n\to\infty}\mu{\bra{\set{x\in X}{|f(x)|\ge n}}}=0$
ただし,$\overline{\R}$は拡大実数である.
$n$を大きくしていくと
- 集合$\set{x\in X}{|f(x)|\ge\frac{1}{n}}$は$f(x)\neq0$なる$x\in X$全体
- 集合$\set{x\in X}{|f(x)|\ge n}$は$X$のほとんど全体
に近付きそうで,(1)も(2)も成り立ちそうなことは直感的に理解できますね.
(1)では$A_n=\set{x\in X}{|f(x)|\ge\frac{1}{n}}$,(2)では$A_n=\set{x\in X}{|f(x)|\ge n}$とみて,それぞれ集合の単調増大列,単調減少列に関する測度の単調収束定理を用います.
(1) $x\in X$が$|f(x)|\ge\frac{1}{n}$を満たせば$|f(x)|\ge\frac{1}{n+1}$を満たすから
\begin{align*}\set{x\in X}{|f(x)|\ge\frac{1}{n}}\subset \set{x\in X}{|f(x)|\ge\frac{1}{n+1}}\end{align*}
が成り立つ.よって,集合の単調増大列に関する測度の単調収束定理より
\begin{align*}&\lim_{n\to\infty}\mu{\bra{\set{x\in X}{|f(x)|\ge\frac{1}{n}}}}
\\&=\mu{\bra{\bigcup_{n=1}^{\infty}\set{x\in X}{|f(x)|\ge\frac{1}{n}}}}
\\&=\mu{\bra{\set{x\in X}{f(x)\neq0}}}\end{align*}
を得る.
(2) $x\in X$が$|f(x)|\ge n+1$を満たせば$|f(x)|\ge n$を満たすから
\begin{align*}\set{x\in X}{|f(x)|\ge n}\supset \set{x\in X}{|f(x)|\ge n+1}\end{align*}
が成り立つ.また,もし$\mu(\set{x\in X}{|f(x)|\ge 1})=\infty$とすると,
\begin{align*}&\int_{X}|f(x)|\,d\mu(x)\ge\int_{\{|f|\ge1\}}|f(x)|\,d\mu(x)
\\&\ge\int_{\{|f|\ge1\}}1\,d\mu(x)=\mu(\set{x\in X}{|f(x)|\ge 1})=\infty\end{align*}
となって$f$が可積分であることに矛盾するから,$\mu(\set{x\in X}{|f(x)|\ge 1})<\infty$である.
よって,集合の単調減少列に関する測度の単調収束定理より
\begin{align*}&\lim_{n\to\infty}\mu{\bra{\set{x\in X}{|f(x)|\ge n}}}
\\&=\mu{\bra{\bigcap_{n=1}^{\infty}\set{x\in X}{|f(x)|\ge n}}}
\\&=\mu{\bra{\set{x\in X}{f(x)=\infty}}}=0\end{align*}
を得る.ただし,最後の等号では,もし$\mu(\set{x\in X}{|f(x)|=\infty})>0$とすると,
\begin{align*}&\int_{X}|f(x)|\,d\mu(x)\ge\int_{\{|f|=\infty\}}|f(x)|\,d\mu(x)
\\&=\infty\cdot\mu{\bra{\set{x\in X}{f(x)=\infty}}}=\infty\end{align*}
となって$f$が可積分であることに矛盾することに注意.
(2)では$f$が可積分であるという仮定は外せません.もし$f$が可積分でないなら,ルベーグ測度空間$(\R,\mathcal{L},m)$で$f(x)=x$とすると,先ほどの補足に注意すると反例になっていることが分かりますね.

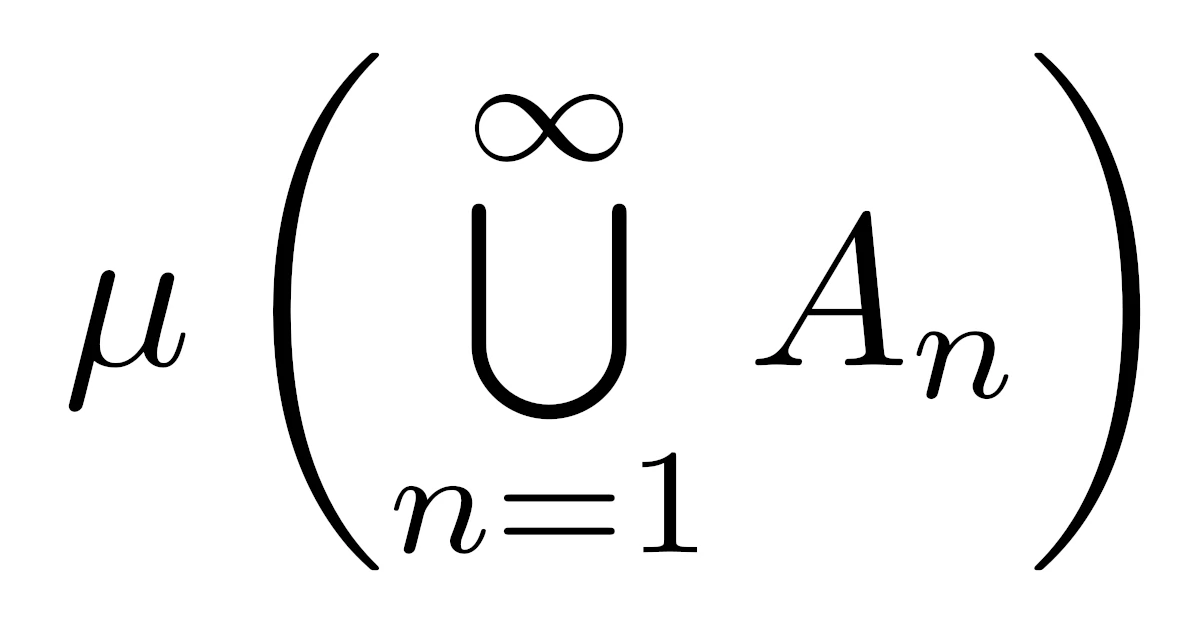
コメント