高校数学では,極限を
「($a$と異なる値をとりながら)$x$を$a$に近付けて$f(x)$が一定の値$p$に限りなく近付くとき,$f(x)$は$p$に収束するといい,$\lim\limits_{x\to a}f(x)=p$と表す」
と学びます.この定義は直観的には分かりやすいものの,「近付ける」という表現が数学的には少々曖昧です.
そこで,大学で学ぶ微分積分学では$\epsilon\text{-}\delta$論法により関数の極限を厳密に定義します.
数列の極限のε-N論法による定義も本質的な考え方は同様です.
この記事では
- 関数の極限の定義($\epsilon\text{-}\delta$論法)
- $\epsilon\text{-}\delta$論法による関数の極限の具体例
- 関数の極限の基本性質
- 3タイプの関数の極限
- 関数の極限の発散
を順に解説します.
関数の極限の定義($\epsilon\text{-}\delta$論法)
まず$\epsilon\text{-}\delta$論法の考え方を説明してから,きちんとした定義を述べます.
関数$f$の値$f(x)$と近付き先$p$との誤差に注目する
例えば,$f(x)=x^2$で定まる関数$f:\R\to\R$を考えましょう.
$x$を$\frac{1}{2}$に近付けると,$f(x)$は$\frac{1}{4}$に近付いていくことがみてとれます.
これは「どんなに小さな正の数$\epsilon$に対しても,十分1/2に近い$x$に対して$f(x)$と1/4の誤差$|f(x)-\frac{1}{4}|$は$\epsilon$未満になる」と言い換えられます.
具体的に$\epsilon=0.1$として,いつ$f(x)$と1/4の誤差$|f(x)-\frac{1}{4}|$は$\epsilon$未満になるかを考えてみましょう.いま
\begin{align*}|f(x)-\frac{1}{4}|=\abs{x^2-\frac{1}{4}}=\abs{x^2-0.25}\end{align*}
ですから,この誤差$|f(x)-\frac{1}{4}|$が$\epsilon=0.1$未満となるのは$\sqrt{0.15}<x<\sqrt{0.35}$のときですね.
つまり,$\sqrt{0.15}<x<\sqrt{0.35}$のとき$|f(x)-\frac{1}{4}|<0.1$となり,下図のように図示できますね.
同じ要領で考えれば,$\epsilon=0.01$なら$\sqrt{0.24}<x<\sqrt{0.26}$のとき$|f(x)-\frac{1}{4}|<\epsilon$となりますし,もっと小さい$\epsilon=0.0001$でも$\sqrt{0.2499}<x<\sqrt{0.2501}$のとき$|f(x)-\frac{1}{4}|<\epsilon$となりますね.
ここで大切なことは,どんなに小さな正の数$\epsilon$に対しても,十分小さい正の数$\delta$があって,$0<|x-\frac{1}{2}|<\delta$のとき$|f(x)-\frac{1}{4}|<\epsilon$となってくれるという点です.
たとえば
- $\epsilon=0.1$なら$\delta=\frac{1}{2}-\sqrt{0.15}$
- $\epsilon=0.01$なら$\delta=\frac{1}{2}-\sqrt{0.24}$
- $\epsilon=0.0001$なら$\delta=\frac{1}{2}-\sqrt{0.2499}$
ととれますね.
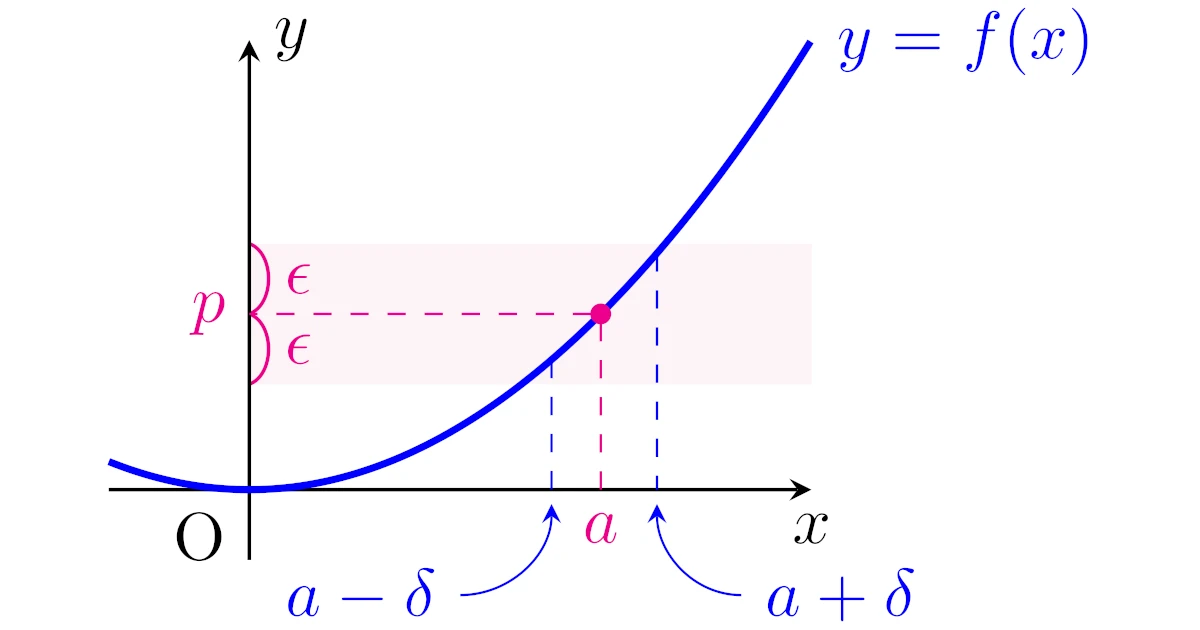
$\epsilon\text{-}\delta$論法による実数値関数の収束の定義
以上の考え方をふまえて$\epsilon\text{-}\delta$論法により実数値関数の収束を定義しましょう.
$a\in\R$とし,$a$の除外近傍で定義された実数値関数$f$を考える.$f(x)$が$x\to a$で収束するとは,ある$p\in\R$が存在して,任意の$\epsilon>0$に対して,ある$\delta>0$が存在して,
\begin{align*}0<|x-a|<\delta\Ra|f(x)-p|<\epsilon\end{align*}
が成り立つことをいう.また,このとき$p$を極限値といい,$\lim\limits_{x\to a}f(x)=p$や$f(x)\to p\ (x\to a)$などと表す.
$a$の除外近傍とは$a$を含む開集合から$a$を除いてできる集合のことをいいます.よって,関数の極限$\lim\limits_{x\to a}f(x)$を考える際は$f(a)$が定義されていなくても問題ありません.
少し砕けた言い方をすれば,「どんなに小さい正の数$\epsilon$に対しても,十分小さい正の数$\delta$をうまくとって,$0<|x-a|<\delta\Ra|f(x)-p|<\epsilon$が成り立つようにできる」ときに,$f(x)$が$p$に収束するというわけですね.
$\epsilon$と$\delta$を用いて表現することが多いことから,この実数値関数の収束の定義の論法を$\epsilon\text{-}\delta$論法といいます.
また,上の考え方からも分かるように,$\delta$は$\epsilon$に応じて決めてよいという点は大切です.
$\epsilon\text{-}\delta$論法による関数の極限の具体例
いくつか具体例を考えましょう.
具体例1($\lim\limits_{x\to3}(\frac{1}{3}x+1)$)
関数$f:\R\to\R$を$f(x)=\frac{1}{3}x+1$で定める.このとき,極限$\lim\limits_{x\to3}f(x)=2$が成り立つことを,$\epsilon\text{-}\delta$論法により示せ.
この問題では$0<|x-3|<\delta$のとき
\begin{align*}|f(x)-2|=\abs{\frac{1}{3}x-1}=\frac{|x-3|}{3}<\frac{\delta}{3}\end{align*}
となります.よって,$\epsilon>0$に対して$0<|x-3|<\delta$のときに$|f(x)-2|<\epsilon$が成り立つには,$\delta=3\epsilon$ととれば良いですね.
任意に$\epsilon>0$をとる.この$\epsilon$に対して,$\delta:=3\epsilon$とおく.$0<|x-3|<\delta$のとき
\begin{align*}|f(x)-2|=\abs{\frac{1}{3}x-1}=\frac{|x-3|}{3}<\frac{\delta}{3}=\epsilon\end{align*}
が成り立つ.よって,$\lim\limits_{x\to3}(\frac{1}{3}x+1)=2$が成り立つ.
このように$\epsilon\text{-}\delta$論法を用いた関数の収束の証明では,どのように$\delta$をとれば$0<|x-a|<\delta\Ra|f(x)-p|<\epsilon$が成り立つかを考えることがポイントとなります.
答案の中では$\delta$を先に定めて$0<|x-3|<\delta\Ra|f(x)-2|<\epsilon$を示していますが,思考プロセスは
- $|f(x)-2|=\frac{|x-3|}{3}<\frac{\delta}{3}$
- $\frac{\delta}{3}=\epsilon$となる$\delta>0$をとればよい
- $\delta:=3\epsilon$とすればよい
の順番になっていることに注意してください.
具体例2($\lim\limits_{x\to1}\frac{(x-1)^2}{x-1}$)
関数$f:\R\setminus\{1\}\to\R$を
\begin{align*}f(x)=\frac{(x-1)^2}{x-1}\end{align*}
で定める.このとき,極限$\lim\limits_{x\to1}f(x)=0$が成り立つことを,$\epsilon\text{-}\delta$論法により示せ.
この問題では$0<|x-1|<\delta$のとき,
\begin{align*}|f(x)-0|=\abs{\frac{(x-1)^2}{x-1}}=|x-1|<\delta\end{align*}
となります.よって,$\epsilon>0$に対して$0<|x-1|<\delta$のときに$|f(x)-0|<\epsilon$が成り立つには,$\delta=\epsilon$ととれば良いですね.
任意に$\epsilon>0$をとる.この$\epsilon$に対して,$\delta:=\epsilon$とおく.$0<|x-1|<\delta$のとき
\begin{align*}|f(x)-0|=\abs{\frac{(x-1)^2}{x-1}}=|x-1|<\delta=\epsilon\end{align*}
が成り立つ.よって,$\lim\limits_{n\to1}f(x)=0$が成り立つ.
$x\to a$の極限では$0<|x-a|<\delta$のときを考えるので,$x\neq a$で$x$を考えることになります.そのため,この問題のように$x\to a$の極限では$f(a)$が定義されていなくても良いですし,定義されていても$f(a)$の値は極限に影響しません.
具体例3(有理数と無理数で場合分けされた関数$f$の極限)
関数$f:\R\to\R$を
\begin{align*}f(x)=\begin{cases}x,&x\in\Q,\\1,&x\notin\Q\end{cases}\end{align*}
で定める.このとき,極限$\lim\limits_{x\to1}f(x)=1$が成り立つことを,$\epsilon\text{-}\delta$論法により示せ.
$\Q$は有理数全部の集合を表します.よって,この問題の関数$f$は有理数$x$に対して$f(x)=x$,無理数$x$に対して$f(x)=1$となる関数です.
この問題では$0<|x-1|<\delta$のとき,
- $x\in\Q$なら$|f(x)-1|=|x-1|<\delta$
- $x\notin\Q$なら$|f(x)-1|=0$
となります.よって,$\epsilon>0$に対して$0<|x-1|<\delta$のときに$|f(x)-1|<\epsilon$が成り立つには,$\delta=\epsilon$とすれば良いですね.
任意に$\epsilon>0$をとる.この$\epsilon$に対して,$\delta:=\epsilon$とおく.$0<|x-1|<\delta$のとき,$x\in\Q$なら
\begin{align*}|f(x)-1|=|x-1|<\delta=\epsilon\end{align*}
が成り立ち,$x\notin\Q$なら
\begin{align*}|f(x)-1|=0<\epsilon\end{align*}
が成り立つ.すなわち,$0<|x-1|<\delta$のとき($x\in\Q$か否かによらず)$|f(x)-1|<\epsilon$が成り立つ.よって,$\lim\limits_{n\to0}f(x)=1$が成り立つ.
関数の極限の基本性質
高校数学では直観的な関数の極限の性質は証明せず認めて使うことが多いのですが,これは関数の極限の定義が曖昧なためきちんと証明することができないのが理由です.
ここでは,高校数学では認めて使っていた性質も$\epsilon\text{-}\delta$論法からきちんと証明しましょう.
関数の極限値が存在すればただ1つに定まる
$a\in\R$とし,$a$の除外近傍で定義された実数値関数$f$を考える.$f(x)$が$x\to a$で収束するとき,極限値$\lim\limits_{x\to a}f(x)$は一意である.
$x\to a$のときの$f(x)$の極限値$p_1,p_2$を任意にとる.また,任意に$\epsilon>0$をとる.このとき,ある$\delta_1,\delta_2>0$が存在して,
\begin{align*}&0<|x-a|<\delta_1\Ra|f(x)-p_1|<\epsilon,
\\&0<|x-a|<\delta_2\Ra|f(x)-p_2|<\epsilon\end{align*}
が成り立つ.よって,$\delta:=\min\{\delta_1,\delta_2\}$とすると,$0<|x-a|<\delta$のとき,三角不等式と併せて
\begin{align*}|p_1-p_2|=|(p_1-f(x))+(f(x)-p_2)|\le|p_1-f(x)|+|f(x)-p_2|<2\epsilon\end{align*}
が成り立つ.$\epsilon$の任意性より$|p_1-p_2|=0$となり$p_1=p_2$が従う.よって,極限値$\lim\limits_{x\to a}f(x)$は一意である.
$\epsilon=0.000001$などいくらでも0に近い正の数に対して$|A|<2\epsilon$が成り立つわけですから,それは$A=0$ということですね.
「好きに2つとってきたのにそれらが一致するなら,もとから1つしかない」という論法ですね.背理法的に「2個以上存在すると仮定して,異なる2つをとってきたが一致することが証明できるので矛盾」と考えてもよいです.
また,$A=0$を示すには「『任意の$\epsilon>0$に対して$|A|<C\epsilon$が成り立つ($C$は正定数)』が証明できればよい」というのはよく用いる論法なので知っておきましょう.
関数の定数倍・和・積の極限
$a\in\R$とし,$a$の除外近傍で定義された実数値関数$f$, $g$を考える.極限値$p=\lim\limits_{x\to a}f(x)$, $q=\lim\limits_{x\to a}g(x)$が存在するとき,
\begin{align*}&\lim_{x\to a}kf(x)=kp,
\\&\lim_{x\to a}(f(x)+g(x))=p+q,
\\&\lim_{x\to a}f(x)g(x)=pq\end{align*}
が成り立つ.ただし,$k\in\R$は任意の定数である.
任意に$\epsilon>0$をとる.
関数の定数倍の極限の証明
$k\neq0$のときは,$p=\lim\limits_{x\to a}f(x)$より,ある$\delta>0$が存在して,
\begin{align*}0<|x-a|<\delta\Ra|f(x)-p|<\frac{\epsilon}{k}\end{align*}
が成り立つ.よって,$0<|x-a|<\delta$のとき,
\begin{align*}|kf(x)-kp|=|k||f(x)-p|<k\cdot\frac{\epsilon}{k}=\epsilon\end{align*}
が成り立つ.一方,$k=0$のときは,$\delta=1$として
\begin{align*}0<|x-a|<\delta\Ra|0f(x)-0p|=0<\epsilon\end{align*}
が成り立つ.したがって,($k=0$のときも$k\neq0$のときも)$\epsilon\text{-}\delta$論法による関数の極限の定義から,$\lim\limits_{x\to a}kf(x)=kp$が従う.
関数の和の極限の証明
$p=\lim\limits_{x\to a}f(x)$, $q=\lim\limits_{x\to a}g(x)$より,ある$\delta_1,\delta_2>0$が存在して,
\begin{align*}&0<|x-a|<\delta_1\Ra|f(x)-p|<\frac{\epsilon}{2},
\\&0<|x-a|<\delta_2\Ra|g(x)-q|<\frac{\epsilon}{2}\end{align*}
が成り立つ.よって,$\delta:=\min\{\delta_1,\delta_2\}$とすると,$0<|x-a|<\delta$のとき,
\begin{align*}|f(x)-p|<\frac{\epsilon}{2}\quad\text{かつ}\quad|g(x)-q|<\frac{\epsilon}{2}\end{align*}
が成り立つから,三角不等式より
\begin{align*}|(f(x)+g(x))-(p+q)|&=|(f(x)-p)+(g(x)-q)|
\\&\le|f(x)-p|+|g(x)-q|
\\&<\frac{\epsilon}{2}+\frac{\epsilon}{2}=\epsilon\end{align*}
が成り立つ.したがって,$\epsilon\text{-}\delta$論法による関数の極限の定義から,$\lim\limits_{x\to a}(f(x)+g(x))=p+q$が従う.
関数の積の極限の証明
$p=\lim\limits_{x\to a}f(x)$, $q=\lim\limits_{x\to a}g(x)$より,ある$\delta_1,\delta_2>0$が存在して,
\begin{align*}&0<|x-a|<\delta_1\Ra|f(x)-p|<\frac{\epsilon}{2|q|},
\\&0<|x-a|<\delta_2\Ra|g(x)-q|<\frac{2|q|\epsilon}{2(2|pq|+\epsilon)}\end{align*}
が成り立つ.よって,$\delta:=\min\{\delta_1,\delta_2\}$とすると,$0<|x-a|<\delta$のとき,
\begin{align*}|f(x)-p|<\frac{\epsilon}{2|q|}\quad\text{かつ}\quad|g(x)-q|<\frac{2|q|\epsilon}{2(2|pq|+\epsilon)}\end{align*}
が成り立つから,三角不等式より
\begin{align*}|f(x)g(x)-pq|&=|f(x)g(x)-f(x)q+f(x)q-pq|
\\&=|f(x)(g(x)-q)+(f(x)-p)q|
\\&\le|f(x)||g(x)-q|+|f(x)-p||q|
\\&<\bra{|p|+\frac{\epsilon}{2|q|}}\cdot\frac{2|q|\epsilon}{2(2|pq|+\epsilon)}+\frac{\epsilon}{2|q|}\cdot|q|
\\&=\frac{\epsilon}{2}+\frac{\epsilon}{2}=\epsilon\end{align*}
が成り立つ.したがって,$\epsilon\text{-}\delta$論法による関数の極限の定義から,$\lim\limits_{x\to a}f(x)g(x)=pq$が従う.
もしかすると「$\epsilon\text{-}\delta$論法の定義は『$0<|x-a|<\delta$なら$|f(x)-p|<\epsilon$』なのに$|f(x)-p|<\frac{\epsilon}{2}$などとしてもいいのか?」と疑問に思うかもしれません.
$\epsilon\text{-}\delta$論法を言葉で説明すれば,「$a$に十分近い$x$だけを考えれば,$f(x)$と$p$の誤差はどんな正の数よりも小さくできる」ということで,$\epsilon$という記号が本質なのではなく,「$f(x)$と$p$の誤差はどんな正の数よりも小さくできる」という点が重要です.
$\frac{\epsilon}{2}>0$ですから,$a$に十分近い$x$だけを考えれば,$f(x)$と$p$の誤差はもちろん$\frac{\epsilon}{2}$よりも小さくできますね.
3タイプの関数の極限
高校数学でも学ぶように,関数の極限はここまでで考えてきた$x\to a$のタイプだけではなく,関数の極限は
- 実数$a$に近付ける極限$x\to a$
- 実数$a$に片側から近付ける極限$x\to a\pm0$
- どこまでも大きく(小さく)する極限$x\to\pm\infty$
の3タイプがあります.極限$x\to a\pm0$と極限$x\to\pm\infty$でも,上で示した基本性質と同様の性質が成り立ちます.
実数$a$に近付ける極限$x\to a$
これは上で考えていた関数の極限です.
(再掲)$a\in\R$とし,$a$の除外近傍で定義された実数値関数$f$を考える.$f(x)$が$x\to a$で収束するとは,ある$p\in\R$が存在して,任意の$\epsilon>0$に対して,ある$\delta>0$が存在して,
\begin{align*}0<|x-a|<\delta\Ra|f(x)-p|<\epsilon\end{align*}
が成り立つことをいう.また,このとき$p$を極限値といい,$\lim\limits_{x\to a}f(x)=p$や$f(x)\to p\ (x\to a)$などと表す.
実数$a$に片側から近付ける極限$x\to a\pm0$
$a$が関数$f$の定義域の端点であるなど,場合によっては片側からのみ$x$を$a$に近付けたいことがあります.
$a\in\R$とし,ある$r>0$が存在して開区間$(a,a+r)$で定義された実数値関数$f$を考える.$f(x)$が$x\to a+0$で収束するとは,ある$p\in\R$が存在して,任意の$\epsilon>0$に対して,ある$\delta>0$が存在して,
\begin{align*}0<x-a<\delta\Ra|f(x)-p|<\epsilon\end{align*}
が成り立つことをいう.また,このとき$p$を極限値といい,$\lim\limits_{x\to a+0}f(x)=p$や$f(x)\to p\ (x\to a+0)$などと表す.
右側極限の$0<x-a<\delta$は$a<x<a+\delta$と同値ですね.この$a<x<a+\delta$の表し方の方が$a$より大きいのが直接的に見てとれて分かりやすいかもしれません.
$a\in\R$とし,ある$r>0$が存在して開区間$(a-r,a)$で定義された実数値関数$f$を考える.$f(x)$が$x\to a-0$で収束するとは,ある$p\in\R$が存在して,任意の$\epsilon>0$に対して,ある$\delta>0$が存在して,
\begin{align*}-\delta<x-a<0\Ra|f(x)-p|<\epsilon\end{align*}
が成り立つことをいう.また,このとき$p$を極限値といい,$\lim\limits_{x\to a-0}f(x)=p$や$f(x)\to p\ (x\to a-0)$などと表す.
右側極限と同様に,左側極限の$-\delta<x-a<0$は$a-\delta$<x<a$と同値で,この$a-\delta<x<a$の表し方の方が$a$より小さいのが直接的に見てとれて分かりやすいかもしれません.
右側極限と左側極限を併せて片側極限といいます.
どこまでも大きく(小さく)する極限$x\to\pm\infty$
数列の極限は$\lim_{n\to\infty}a_n$のように$n$をどこまでも大きくする極限を考えました.
関数の極限でも同様に$x$をどこまでも大きくする極限$x\to\infty$,$x$をどこまでも小さくする極限$x\to-\infty$を定義します.
$\ell\in\R$とし,区間$(\ell,\infty)$で定義された実数値関数$f$を考える.$f(x)$が$x\to\infty$で収束するとは,ある$p\in\R$が存在して,任意の$\epsilon>0$に対して,ある$R>0$が存在して,
\begin{align*}R<x\Ra|f(x)-p|<\epsilon\end{align*}
が成り立つことをいう.また,このとき$p$を極限値といい,$\lim\limits_{x\to\infty}f(x)=p$や$f(x)\to p\ (x\to\infty)$などと表す.
$\ell\in\R$とし,区間$(-\infty,\ell)$で定義された実数値関数$f$を考える.$f(x)$が$x\to-\infty$で収束するとは,ある$p\in\R$が存在して,任意の$\epsilon>0$に対して,ある$R>0$が存在して,
\begin{align*}x<-R\Ra|f(x)-p|<\epsilon\end{align*}
が成り立つことをいう.また,このとき$p$を極限値といい,$\lim\limits_{x\to-\infty}f(x)=p$や$f(x)\to p\ (x\to-\infty)$などと表す.
これらの極限$x\to\pm\infty$は$\epsilon\text{-}\delta$論法というより,数列の極限の$\epsilon\text{-}N$論法に近いですね.
関数の極限の発散
関数の極限はいつでも収束するとは限りません.
関数の極限が発散するとは,収束しないことをいう
$a\in\R$とし,$a$の除外近傍で定義された実数値関数$f$を考える.$f(x)$が$x\to a$で発散するとは,$f(x)$が$x\to a$で収束しないことをいう.
$\epsilon\text{-}\delta$論法的に書けば,「任意の$p\in\R$に対して,ある$\epsilon>0$が存在して,任意の$\delta>0$に対し,
\begin{align*}0<|x-a|<\delta\quad\text{かつ}\quad|f(x)-p|\ge\epsilon\end{align*}
が成り立つ」ということになります.
言葉で説明すれば,「どんな$p\in\R$に対しても,十分小さい$\epsilon>0$をとれば,どんなに小さい$\delta>0$よりも$x$と$a$の誤差が小さくても,$f(x)$と$p$の誤差は$\epsilon$以上になってしまう」ということですね.
どんなに$x$を$a$に近付けても,$f(x)$と$p$の誤差が一定の$\epsilon>0$より大きいのであれば,$f(x)$は$p$に近付いているとは言えませんね.
数列の極限の発散でもそうだったように,関数の極限の発散には3種類あります.
関数の極限が(正の)無限大に発散する($\lim\limits_{x\to a}f(x)=\infty$)
$a$とは異なる$x$を$a$に近付けるとき,$f(x)$がどこまでも大きくなるなら,$f(x)$は$x\to a$で(正の)無限大に発散するといいます.
$a\in\R$とし,$a$の除外近傍で定義された実数値関数$f$を考える.$f(x)$が$x\to a$で(正の)無限大に発散するとは,任意の$L>0$に対して,ある$\delta>0$が存在して,
\begin{align*}0<|x-a|<\delta\Ra f(x)>L\end{align*}
が成り立つことをいう.また,$\lim\limits_{x\to a}f(x)=\infty$や$f(x)\to \infty\ (x\to a)$などと表す.
他のタイプの極限$x\to a\pm0$, $x\to\pm\infty$でも同様に正の無限大への発散を定義します.
関数の極限が負の無限大に発散する($\lim\limits_{x\to a}f(x)=-\infty$)
$a$とは異なる$x$を$a$に近付けるとき,$f(x)$がどこまでも小さくなるなら,$f(x)$は$x\to a$で負の無限大に発散するといいます.
$a\in\R$とし,$a$の除外近傍で定義された実数値関数$f$を考える.$f(x)$が$x\to a$で負の無限大に発散するとは,任意の$L>0$に対して,ある$\delta>0$が存在して,
\begin{align*}0<|x-a|<\delta\Ra f(x)<-L\end{align*}
が成り立つことをいう.また,$\lim\limits_{x\to a}f(x)=-\infty$や$f(x)\to-\infty\ (x\to a)$などと表す.
他のタイプの極限$x\to a\pm0$, $x\to\pm\infty$でも同様に負の無限大への発散を定義します.
関数の極限が振動する
$a$とは異なる$x$を$a$に近付けるとき,$f(x)$が(正の)無限大にも負の無限大にも発散しないなら,$f(x)$は$x\to a$で振動するといいます.
$a\in\R$とし,$a$の除外近傍で定義された実数値関数$f$を考える.$f(x)$が$x\to a$で振動するとは,発散するが(正の)無限大にも負の無限大にも発散しないことをいう.
他のタイプの極限$x\to a\pm0$, $x\to\pm\infty$でも同様に振動を定義します.


コメント