微分積分学では次のボルツァーノ-ワイエルシュトラス（Bolzano-Weierstrass）の定理を学びます．
ボルツァーノ-ワイエルシュトラスの定理を用いることでさまざまな定理を示すことができ，「縁の下の力持ち」という言葉がよく似合う定理です．
単調有界実数列の収束定理を用いて示される区間縮小法（nested intervals）と呼ばれる論法を用いることで，ボルツァーノ-ワイエルシュトラスの定理を証明することができます．
この記事では
- 部分列とボルツァーノ-ワイエルシュトラスの定理
- 区間縮小法と証明
を順に解説します．
「微分積分学の基本」の一連の記事
微分積分学の参考文献
以下は微分積分学に関するオススメの教科書です．
微分積分学（笠原晧司 著）
数学科など理論系の学生向けの微分積分学の入門書です．基本的な例から発展的な例まで扱われており，バランスの良い教科書です．
部分列とボルツァーノ-ワイエルシュトラスの定理
ボルツァーノ-ワイエルシュトラスの定理を説明するために，まずは部分列を定義する必要があります．
部分列の考え方
ざっくり言えば，元の数列$\{a_n\}_{n=1}^{\infty}$から項を間引いてできる数列を部分列と言います．
以下では$n$は正の整数とし，$\{a_n\}_{n=1}^{\infty}$を単に$\{a_n\}_n$と表します．
例えば，数列$\{a_n\}$の偶数番目の項だけからなる数列は
\begin{align*}a_2,\ a_4,\ a_6,\ a_8, a_{10},\dots\end{align*}
となり，この数列は$\{a_{2n}\}_{n}$と表せますね．
他にも数列$\{a_n\}$の素数番目の項だけからなる数列は
\begin{align*}a_2,\ a_3,\ a_5,\ a_7, a_{11},\dots\end{align*}
となり，この数列は$\{a_{n_k}\}_k$（$n_k$は$k$番目の素数）などと表せます．
このように，数列$\{a_n\}_n$の添え字$n$を$n_1<n_2<\dots<n_k<\dots$なる正の整数の列$\{n_k\}_k$で考えてできる数列$\{a_{n_k}\}_k$は，元の数列$\{a_n\}$から項を間引いてできる数列になっていますね．
部分列の定義
いまの考え方をもとに部分列をきちんと定義すると次のようになります．
数列$\{a_n\}_n$, $\{b_n\}_n$を考える．正の整数の狭義単調増加列$\{n_k\}_k$が存在して$\{b_n\}_n=\{a_{n_k}\}_{k}$となるとき，$\{b_n\}_n$は$\{a_n\}_n$の部分列（subsequence）であるという．
$\{b_n\}_n=\{a_{n_k}\}_{k}$を書き並べると
\begin{align*}b_1=a_{n_1},\ b_2=a_{n_2},\ b_3=a_{n_3},\dots\end{align*}
ということですから，数列$\{b_n\}_n$は数列$\{a_n\}_n$から項を間引いてできる数列になっていますね．
ボルツァーノ-ワイエルシュトラスの定理
冒頭でも紹介したように，ボルツァーノ-ワイエルシュトラスの定理は次の通りです．
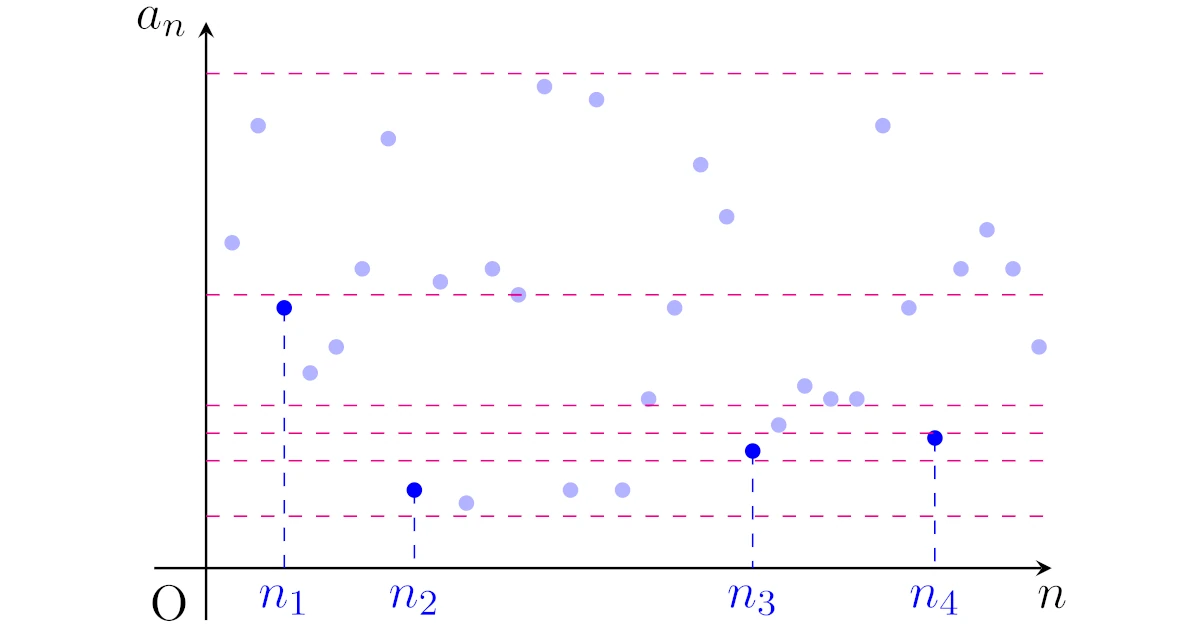
つまり，実数列$\{a_n\}$がどんなに「ぐちゃぐちゃ」な数列であっても，有界でさえあればうまく項$a_{n_1},a_{n_2},a_{n_3},\dots$を選んで収束する部分列$\{a_{n_k}\}_k$をつくることができるということですね．
直観的には，「横」から見ると有界区間上に無限個の点が存在しているので，その中の「濃い」部分に収束する部分列がとれそうですね．実際に証明は本質的にこのアイディアを用いています．
このボルツァーノ-ワイエルシュトラスの定理の証明には区間縮小法（the nested interval method）を用います．
区間縮小法と証明
区間縮小法を証明し，ボルツァーノ-ワイエルシュトラスの定理を証明しましょう．
区間縮小法
以下では，閉区間$I=[a,b]$の長さ$b-a$を$|I|$と表します．
［区間縮小法］有界閉区間$I_1,I_2,I_3,\dots\subset\R$が
\begin{align*}I_1\supset I_2\supset I_3\supset\dots,\quad
\lim_{k\to\infty}|I_k|=0\end{align*}
を満たすとする．
このとき，共通部分$\bigcap\limits_{k=1}^{\infty}I_k$はただ１つの元のみからなり，
\begin{align*}\bigcap_{k=1}^{\infty}I_k=\{\alpha\},\quad
I_{k}=[p_k,q_k]\quad(k=1,2,3,\dots)\end{align*}
とすると，$\lim\limits_{k\to\infty}p_{k}=\lim\limits_{k\to\infty}q_k=\alpha$が成り立つ．
つまり，「区間$I_k$が入れ子状に小さくなっていき，区間$I_k$の長さが０に収束するなら，区間は１点に潰れていく」というわけですね．
区間縮小法の証明
証明には「広義単調増加かつ上に有界な（広義単調減少かつ下に有界な）実数列は収束する」という単調有界実数列の収束定理を用います．
$I_1\supset I_2\supset I_3\supset\dots$より
\begin{align*}p_1\le p_2\le p_3\le\dots\le q_1\end{align*}
なので，実数列$\{p_k\}$は広義単調増加かつ上に有界だから，単調有界実数列の収束定理により収束する．同様に，実数列$\{q_k\}$は広義単調減少かつ下に有界だから，単調有界実数列の収束定理により収束する．
$p=\lim\limits_{k\to\infty}p_k$, $q:=\lim\limits_{k\to\infty}q_k$とおくと，
\begin{align*}\lim_{k\to\infty}|I_{k}|=0&\iff \lim_{k\to\infty}(q_k-p_k)=0
\\&\iff q-p=0\iff p=q\end{align*}
が成り立つ．任意の$k\in\{1,2,\dots\}$に対して，$p_k\le p=q\le q_k$だから$p=q\in I_k$なので$\bigcap\limits_{k=1}^{\infty}I_k$は空でない．
また，集合の共通部分の定義から，任意の$\alpha\in\bigcap\limits_{k=1}^{\infty}I_k$は
\begin{align*}\alpha\in I_k\iff p_k\le\alpha\le q_k\quad(k=1,2,3,\dots)\end{align*}
を満たすから，$k\to\infty$とすれば極限について$p\le\alpha\le q$が成り立つ．
よって，$p=q=\alpha$なので$\bigcap\limits_{k=1}^{\infty}I_{k}$はただ１つの元$\alpha$のみからなり，$\alpha$は$\{p_k\}$, $\{q_k\}$の極限に一致する．
ボルツァーノ-ワイエルシュトラスの定理の証明
有界なので$p_0\le a_n\le q_0$（$n=1,2,\dots$）となる$p_0,q_0\in\R$が存在し，この$[p_0,q_0]$を半分半分に狭めていけば収束する部分列が作れることが分かります．
有界実数列$\{a_n\}$をとる．このとき，有界性よりある$p_0,q_0\in\R$が存在して$p_0\le a_n\le q_0$が成り立つ．
ステップ１：単調増加列$\{p_k\}$と単調減少列$\{q_k\}$を構成する
$r_0:=\dfrac{p_0+q_0}{2}$とおく．
このとき，区間$[p_0,r_0]$, $[r_0,q_0]$の少なくとも一方には実数列$\{a_n\}$の項が無限に属する（もしどちらにも有限個しかなければ，実数列$\{a_n\}$の項が有限個しか存在しないことになり矛盾）から
- $[p_0,r_0]$に実数列$\{a_n\}$の項が無限に属していれば$p_1:=p_0$, $q_1:=r_0$
- そうでないときは$p_1:=r_0$, $q_1:=q_0$
と定め，さらに$r_1:=\dfrac{p_1+q_1}{2}$と定める．
同様に，
- $[p_1,r_1]$に実数列$\{a_n\}$の項が無限に属していれば$p_2:=p_1$, $q_2:=r_1$
- そうでないときは$p_2:=r_1$, $q_2:=q_1$
と定め，さらに$r_2:=\dfrac{p_2+q_2}{2}$と定める．
これを帰納的に繰り返し，有界閉区間$I_{k}=[p_{k},q_{k}]$（$k=0,1,2,\dots$）を作ると$I_{0}\supset I_{1}\supset I_{2}\supset\dots$かつ$\lim\limits_{k\to\infty}|I_{k}|=0$が成り立つ．
よって，区間縮小法により$\lim\limits_{k\to\infty}p_{k}=\lim\limits_{k\to\infty}q_{k}$を得る．
ステップ２：収束する部分列を構成する
数列$\{a_n\}$の部分列$\{a_{n_k}\}$を
- 数列$\{a_n\}$の$I_1$に属する最初の項を$a_{n_{1}}$
- 数列$\{a_n\}$の$a_{n_1}$より後の$I_2$に属する最初の項を$a_{n_2}$
- 数列$\{a_n\}$の$a_{n_2}$より後の$I_3$に属する最初の項を$a_{n_3}$
- ……
と定める．
このとき，$a_{n_{k}}\in I_{k}$より$p_{k}\le a_{n_{k}}\le q_{k}$となるので，はさみうちの原理より$\{a_{n_{k}}\}$は極限をもつ．
コメント