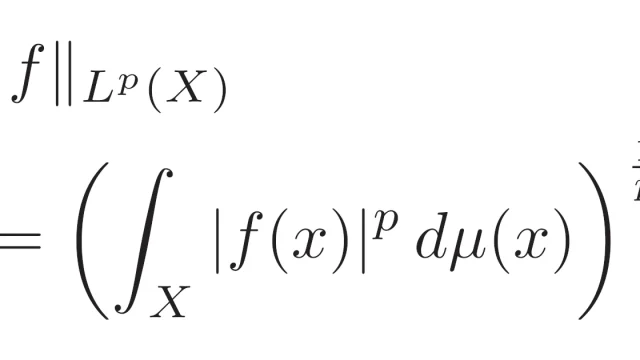ルベーグ空間 ルベーグ空間（Lᵖ空間）｜ルベーグ積分に関するノルム・内積
測度空間Xに対して，Xでp乗可積分な関数の（商）空間をLᵖ(X)と表します．この記事ではLᵖ(X)の正確な定義を説明し，LᵖノルムによってLᵖ(X)がノルム空間・内積空間となることを解説します．
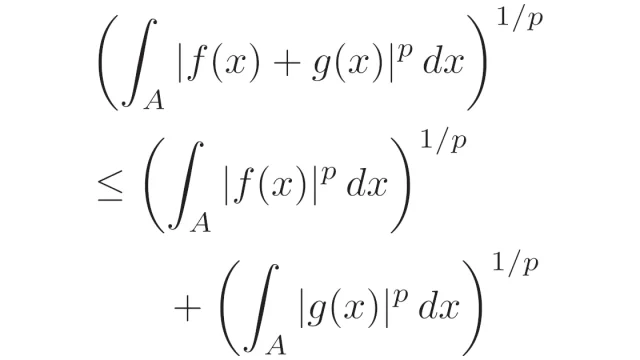ルベーグ空間 ミンコフスキーの不等式と証明｜便利な積分形も併せて紹介
ルベーグ積分（測度論）を扱う分野では「ミンコフスキーの不等式」がよく用いられます．この記事では，和のミンコフスキーの不等式と併せて，積分形のミンコフスキーの不等式も紹介します．
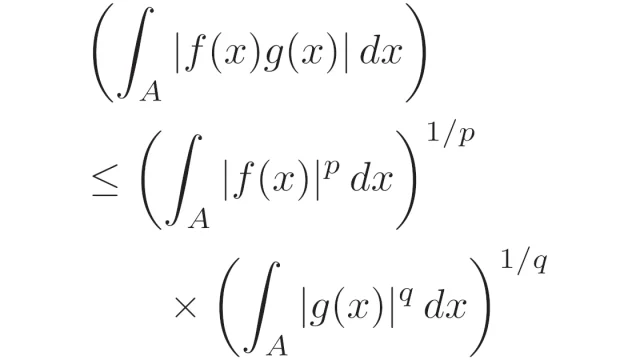ルベーグ空間 ヘルダーの不等式の証明・応用｜ルベーグ積分の基本不等式
ルベーグ積分（測度論）を扱う分野では「ヘルダーの不等式」は基本的な不等式のひとつとして重要です．この記事では，ヘルダーの不等式の証明と，ヘルダーの不等式の応用（双対性）を説明します．
ルベーグ空間 本質的有界な関数のルベーグ空間L^∞｜ノルム空間として定義
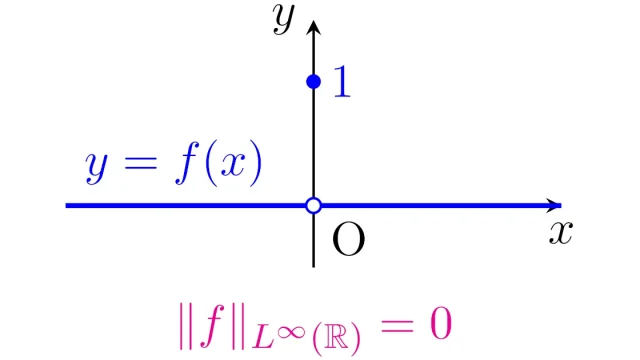
（適切な同一視のもとで）本質的有界な可測関数全部の集合L^∞はバナッハ空間（完備なノルム空間）となります．この空間L^∞を「ルベーグ空間」と言います．
ルベーグ空間 本質的有界な可測関数｜本質的上限(ess sup)・下限(ess inf)
関数の上限は１点の値を変えることでどこまでも大きくすることができますが，そのような上限は本質的な上限とは言い難いですね．この記事では本質的上限と本質的下限の定義・具体例・性質を説明します．