大雑把に言えば,関数$f$を$p$乗した関数が積分可能であるとき$f$は$p$乗可積分であるといい,$p$乗可積分関数全部の集合を$L^p$と表して,文字通り$L^p$ 空間などと呼びます($1\le p<\infty$).
詳しく言えば,測度空間$(X,\mathcal{F},\mu)$に対して,
\begin{align*}\int_{X}|f(x)|^p\,d\mu(x)<\infty\end{align*}
を満たす$X$上で定義された可測関数$f$全部の集合で,ほとんど至る所等しい関数たちを同一視してできる空間を$L^p(X)$と表します.
$L^p(X)$を扱う大きなメリットのひとつは,ノルムもしくは内積に関して完備性をもつことです.
この記事ではノルム空間となることまで証明し,完備性はのちの記事(準備中)で証明します.
とくに測度空間$(X,\mathcal{F},\mu)$がルベーグ測度空間の部分測度空間であるとき,$L^p(X)$をルベーグ空間と呼びます.
この記事では
- 可測関数を同一視してできる線形空間
- ルベーグ空間$L^p$の定義($1\le p<\infty$)
- 補足(複素数値関数の場合の$L^2$内積)
を順に解説します.
「ルベーグ空間$L^p$の基本」の一連の記事
可測関数を同一視してできる線形空間
ルベーグ積分においては,ほとんど至る所で等しい関数は積分すると同じ値となるので,同じ関数とみなしたいところです.
そこで,ルベーグ空間$L^p$をきちんと定義するために,ほとんど至る所で等しい関数を同一視する同値関係(商集合)を考える必要があります.
これは本質的有界な関数全部のルベーグ空間$L^\infty$の場合と同様なので,この記事では簡潔な説明に留めることにします.証明など詳しくは以下の記事を参照してください.
本質的に等しい可測関数の同一視
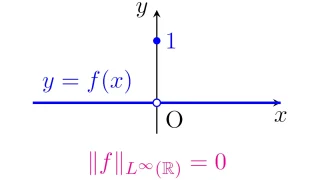
一般に測度空間$(X,\mathcal{F},\mu)$の零集合(測度0の集合)上でのみ異なっている2つの関数$f$, $g$は$X$上ほとんど至る所で等しいと言うのでした.
$X$上の本質的上限を表す$\|\cdot\|_{L^\infty(X)}$を用いると,2つの関数$f,g:X\to\R$が$X$上ほとんど至る所で等しいことは,$\|f-g\|_{L^\infty(X)}=0$と表すことができますね.
そこで,ほとんど至る所で等しいルベーグ可測関数を同一視してできる空間を考えましょう.
ルベーグ可測集合$X\subset\R^d$上のルベーグ可測関数全部の集合に,関係$\sim$を
\begin{align*}f\sim g\stackrel{\mathrm{def.}}{\iff}m(\set{x\in X}{f(x)\neq g(x)})=0\end{align*}
つまり,ほとんど至る所で等しい関数たちを同一視する同値関係$\sim$が定まるというわけですね.
和とスカラー倍
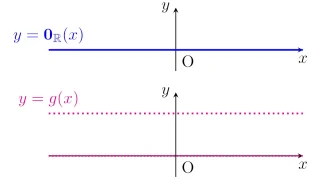
ルベーグ可測集合$X\subset\R^d$上のルベーグ可測関数全部の集合を$L(X)$で表すと,$L(X)$は通常の和・スカラー倍によって線形空間となりますね.
また,$L(X)$を同値関係$\sim$で割ってできる商空間$L(X)/\sim$を$\tilde{L}(X)$で表すことにしましょう.
商空間$\tilde{L}(X)$上の和・スカラー倍を$L(X)$上の和・スカラー倍から自然に定めることにより,$\tilde{L}(X)$も線形空間となります.
ルベーグ可測集合$X\subset\R^d$に対して,$\tilde{L}(X)$上の演算+と作用・を
- $F,G\in\tilde{L}(X)$に対して,代表元$f\in F$, $g\in G$をとり,$L(X)$上の関数の和$f+g$が属する同値類を$F+G$
- $F\in\tilde{L}(X)$, $k\in\R$に対して,代表元$f\in F$をとり,$L(X)$上の関数のスカラー倍$kf$が属する同値類を$k\cdot F$
と定めることができ,+, ・それぞれを和・スカラー倍として$\tilde{L}(X)$は実線形空間となる.
$L(X)$上の零ベクトルは「恒等的に値0をとる関数」で,$\tilde{L}(X)$上の零ベクトルは「恒等的に値0をとる関数とほとんど至る所で等しい関数」ですね.
ルベーグ空間$L^p$の定義(${1\le p<\infty}$)
上の準備のもとで,ルベーグ空間$L^p$を定義しましょう.
$p$乗可積分関数の同値類
同値関係$\sim$で割る前の$L(X)$に属するルベーグ可測関数$f$が$p$乗ルベーグ可積分であれば,$f\sim g$となるルベーグ可測関数$g$も$p$乗ルベーグ可積分となります.
$p\in[1,\infty)$とし,可測集合$X\subset\R^d$を考える.$F\in\tilde{L}(X)$のある代表元$f$が$X$上で$p$乗ルベーグ可積分なら,任意の$g\in F$に対して,
\begin{align*}\int_{X}|f(x)|^p\,dx=\int_{X}|g(x)|^p\,dx<\infty\end{align*}
が成り立つ.
$\tilde{L}(X)$は商集合なので,$F\in\tilde{L}(X)$は$L(X)$の部分集合であることに注意しましょう.
$f$, $g$は同じ同値類$F$に属するから,$f$, $g$は$X$上ほとんど至る所で等しい.よって,$|f|^p$, $|g|^p$も$X$上ほとんど至る所で等しいから,
\begin{align*}\int_{X}|f(x)|^p\,dx=\int_{X}|g(x)|^p\,dx\end{align*}
が成り立つ.$f$は$X$上で$p$乗ルベーグ可積分だから,$\int_{X}|f(x)|^p\,dx<\infty$なので,
\begin{align*}\int_{X}|g(x)|^p\,dx<\infty\end{align*}
も成り立つ.
$\tilde{L}(X)$の同値類は関数たちの集合なので本来の関数ではありませんが,いまの命題のように$\tilde{L}(X)$の同じ同値類に属する関数たちの積分は同じ値となるので,一般に$\tilde{L}(X)$の同値類も通常の関数のように扱います.
この記事でも,以下では$p$乗ルベーグ可積分関数が属する同値類$F\in\tilde{L}(X)$を通常の$p$乗ルベーグ可積分関数のように扱います.
ルベーグ空間$L^p$の定義
次の補題の空間$L^p(X)$をルベーグ空間といいます.
$p\in[1,\infty)$とし,ルベーグ可測集合$X\subset\R^d$を考える.$X$上で$p$乗ルベーグ可積分な関数$f\in\tilde{L}(X)$全部の集合$L^p(X)$は,$\tilde{L}(X)$の線形部分空間となる.さらに,
\begin{align*}\|f\|_{L^p(X)}:=\bra{\int_{X}|f(x)|^p\,dx}^{1/p}<\infty\end{align*}
で定まる$\|\cdot\|_{L^p(X)}:L^p(X)\to\R$は$L^p(X)$上のノルムである.
$X$上で恒等的に値0をとる関数を$0_{X}$と表す.
$L^p(X)$が部分空間となることの証明
線形部分空間の定義(もしくは必要十分条件)より
- $L^p(X)\neq\emptyset$
- $L^p(X)$が和で閉じていること
- $L^p(X)$がスカラー倍で閉じていること
を示せばよい.
$\int_{X}|0_{X}|^p(x)\,dx=0$だから$0_{X}$は$X$上$p$乗ルベーグ可積分なので,$L^p(X)\neq\emptyset$である.
任意に$f,g\in L^p(X)$と$k\in\R$をとる.$\|f\|_{L^p(X)}<\infty$, $\|g\|_{L^p(X)}<\infty$なので,ミンコフスキーの不等式より
\begin{align*}\|f+g\|_{L^p(X)}\le\|f\|_{L^p(X)}+\|g\|_{L^p(X)}<\infty\quad\dots(*)\end{align*}
が従う.また,$\|f\|_{L^p(X)}<\infty$なので,$\|f\|_{L^p(X)}$の定義より
\begin{align*}\|kf\|_{L^p(X)}&=\bra{\int_{X}|kf(x)|^p\,dx}^{1/p}=\bra{|k|^p\int_{X}|f(x)|^p\,dx}^{1/p}
\\&=|k|\bra{\int_{X}|f(x)|^p\,dx}^{1/p}=|k|\|f\|_{L^p(X)}<\infty\quad\dots(**)\end{align*}
が従う.よって,$L^p(X)$が$\tilde{L}(X)$の和・スカラー倍により閉じているから,$L^p(X)$は$\tilde{L}(X)$の線形部分空間である.
$\|\cdot\|_{L^p(X)}$がノルムとなることの証明
劣加法性はミンコフスキーの不等式$(**)$そのものであり,斉次性は$(*)$により示されている.よって,あとは残る非退化性を示せばよい.
$L^p(X)$上の零ベクトルは$0_{X}$(とほとんど至る所で等しい関数の同値類)であり,
\begin{align*}\|0_{X}\|_{L^p(X)}=\bra{\int_{X}|0_{X}|^p\,dx}^{1/p}=0^{1/p}=0\end{align*}
が成り立つ.
逆に$f$が$L^p(X)$上の零ベクトルでないとすると,
\begin{align*}B:=\set{x\in X}{f(x)\neq0}\end{align*}
は$m(B)>0$を満たす($f$はルベーグ可測関数だから$B$はルベーグ可測集合であることに注意).また
\begin{align*}B_n:=\set{x\in X}{|f(x)|\ge\frac{1}{n}}\quad(n=1,2,\dots)\end{align*}
とすると$B=\bigcup_{n=1}^{\infty} B_n$である.$B_n\subset B_{n+1}$と併せて
\begin{align*}\lim_{n\to\infty}m(B_n)=m(B)\end{align*}
が成り立つ.よって,ある$N\in\N$が存在して$m(B_N)>\frac{1}{2}m(B)>0$となるから,
\begin{align*}\|f\|_p&\ge\bra{\int_{B_N}|f(x)|^p\,dx}^{1/p}\ge\bra{\int_{B_N}\frac{1}{N^p}\,dx}^{1/p}
\\&=\bra{\frac{1}{N^p}m(B_N)}^{1/p}=\frac{1}{N}m(B_N)^{1/p}>0\end{align*}
となって,$\|f\|_p\neq0$が従う.
ノルム$\|f\|_{L^p(X)}$の定義で全体を1/p乗しているのは,斉次性$\|kf\|_p=|k|\|f\|_p$が成り立つようにするためですね.
これでノルム空間としてのルベーグ空間$L^p(X)$が次のように定義できることが分かりました.
$p\in[1,\infty)$とし,ルベーグ可測集合$X\subset\R^d$を考える.$\tilde{L}(X)$の$p$乗ルベーグ可積分関数全部の部分空間
\begin{align*}&\set{f\in\tilde{L}(X)}{\|f\|_{L^p(X)}<\infty},
\\&\|f\|_{L^p(X)}:=\bra{\int_{X}|f(x)|^p\,dx}^{1/p}\end{align*}
のノルム$\|\cdot\|_{L^p(X)}$を備えたノルム空間をルベーグ空間(Lebesgue space)といい,$L^p(X)$と表す.
このノルム$\|\cdot\|_{L^p(X)}$を$L^p$ノルムといいます.$L^p$ノルムはもとから$1/p$乗されているので,$p$乗すれば
\begin{align*}\|f\|_{L^p(X)}^p=\int_{X}|f(x)|^p\,dx\end{align*}
となることは当たり前にしておきましょう.
内積空間としての$L^2$
実は$p=2$の場合のルベーグ空間$L^p$は自然に内積空間となります.
このことを示すために,次の線形代数学の一般論を確認しておきましょう.
実ノルム空間$(V,\|\cdot\|)$に対して,次は同値である.
- 任意の$\m{u},\m{v}\in V$に対して
\begin{align*}\|\m{u}+\m{v}\|^2+\|\m{u}-\m{v}\|^2=2(\|\m{u}\|^2+\|\m{v}\|^2)\end{align*}
が成り立つ. - $(\cdot,\cdot):V\times V\to\R$を
\begin{align*}(\m{u},\m{v})=\frac{1}{4}(\|\m{u}+\m{v}\|^2-\|\m{u}-\m{v}\|^2)\end{align*}
で定めると,$(\cdot,\cdot)$が$V$上の内積となる.
さらに,これらのいずれか一方(したがって両方)を満たすとき,任意の$\m{u}\in V$に対して$(\m{u},\m{u})=\|\m{u}\|^2$が成り立つ.
(1)の等式を中線定理ということから,この補題は標語的に「ノルム空間が内積空間となるための必要十分条件は,中線定理が成り立つことである」と言いますね.
この補題を用いると,上で定めた$L^2$ノルムにより,$L^2$の内積が自然に定まることが分かります.
ルベーグ可測集合$X\subset\R^d$に対して,ルベーグ空間$L^2(X)$は
\begin{align*}(f,g)=\int_{X}f(x)g(x)\,dx\end{align*}
で定まる内積$(\cdot,\cdot):L^2(X)\times L^2(X)\to\R$により内積空間となり,このときのノルムは$L^2$ノルム$\|\cdot\|_{L^2(X)}$である.
任意の$f,g\in L^2(X)$に対して,
\begin{align*}&\|f+g\|_{L^2(X)}^2+\|f-g\|_{L^2(X)}^2
\\&=\int_{X}|f(x)+g(x)|^2\,dx+\int_{X}|f(x)-g(x)|^2\,dx
\\&=2\int_{X}(f(x)^2+g(x)^2)\,dx
\\&=2\bra{\int_{X}|f(x)|^2\,dx+\int_{X}|g(x)|^2\,dx}
\\&=2(\|f\|_{L^2(X)}^2+\|g\|_{L^2(X)}^2)\end{align*}
が成り立つから,補題より$L^2(X)$は
\begin{align*}(f,g)&=\frac{1}{4}(\|f+g\|_{L^2(X)}^2-\|f-g\|_{L^2(X)}^2)
\\&=\frac{1}{4}\bra{\int_{X}|f(x)+g(x)|^2\,dx-\int_{X}|f(x)-g(x)|^2\,dx}
\\&=\int_{X}f(x)g(x)\,dx\,dx\end{align*}
で定まる$(\cdot,\cdot):L^2(X)\times L^2(X)\to\R$を内積として内積空間となる.
この内積を$L^2$内積といいます.
補足(複素数値関数の場合の$L^2$内積)
以上は関数が実数値の場合で,複素数値の場合もほとんど並行してルベーグ空間$L^p$が定義され,ノルムの形は実数値の場合と同じです.
しかし,$L^2$内積について少し事情が変わります.これは線形代数学の一般論として挙げた補題が,複素ノルム空間の場合に次のように変わることに起因します.
複素ノルム空間$(V,\|\cdot\|)$に対して,次は同値である.
- 任意の$\m{u},\m{v}\in V$に対して
\begin{align*}\|\m{u}+\m{v}\|^2+\|\m{u}-\m{v}\|^2=2(\|\m{u}\|^2+\|\m{v}\|^2)\end{align*}
が成り立つ. - $(\cdot,\cdot):V\times V\to\R$を
\begin{align*}(\m{u},\m{v})=\frac{1}{4}(\|\m{u}+\m{v}\|^2-\|\m{u}-\m{v}\|^2+i\|\m{u}+i\m{v}\|^2-i\|\m{u}-i\m{v}\|^2)\end{align*}
で定めると,$(\cdot,\cdot)$が$V$上の内積となる.
さらに,これらのいずれか一方(したがって両方)を満たすとき,任意の$\m{u}\in V$に対して$(\m{u},\m{u})=\|\m{u}\|^2$が成り立つ.
この補題に従えば,複素数値関数の場合のルベーグ空間$L^2$は次のようになります.
ルベーグ可測集合$X\subset\C^d$に対して,ルベーグ空間$L^2(X)$は
\begin{align*}(f,g)=\int_{X}f(x)\overline{g(x)}\,dx\end{align*}
で定まる内積$(\cdot,\cdot):L^2(X)\times L^2(X)\to\C$により内積空間となり,このときのノルムは$L^2$ノルム$\|\cdot\|_{L^2(X)}$である.
すなわち,内積の第2成分にある関数が複素共役となります.これは$\C^n$の標準内積が
\begin{align*}\bmat{x_1\\\vdots\\x_n}\cdot\bmat{y_1\\\vdots\\y_n}=\sum_{k=1}^{n}x_k\overline{y_k}\end{align*}
であることから類推すれば納得できるでしょう.
証明は実ノルムの場合とほとんど同じなので,読者の皆さんにお任せします.

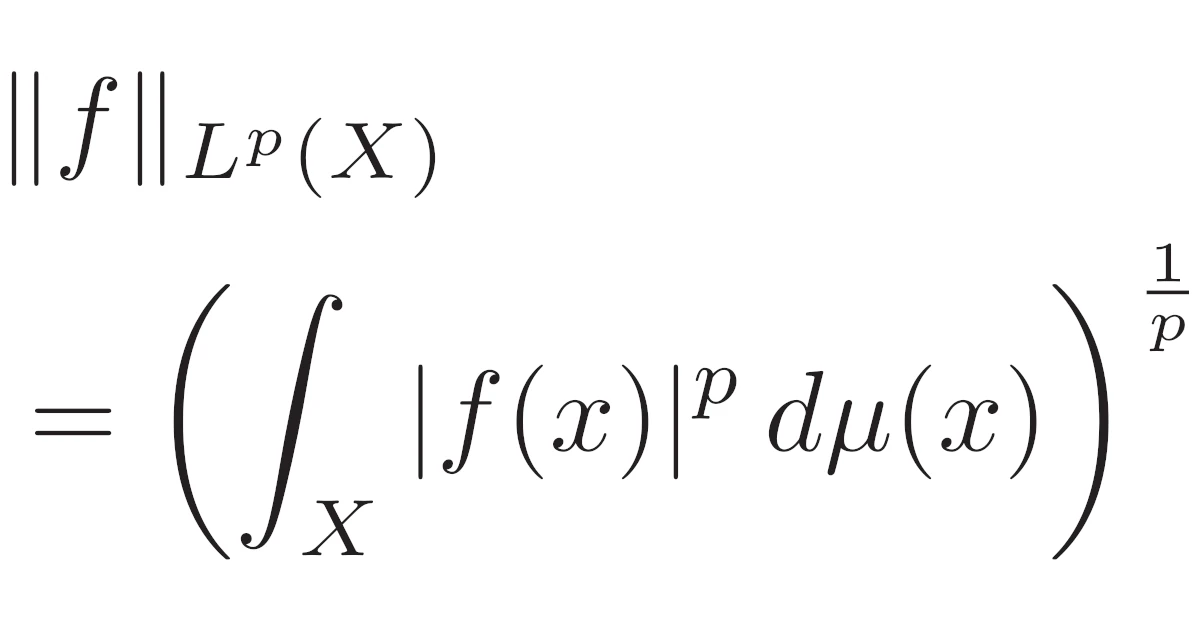


コメント