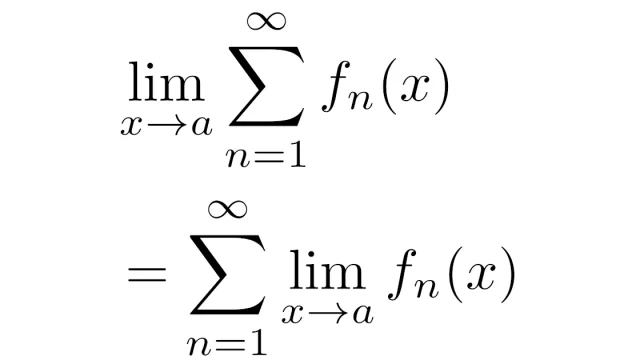 測度論
測度論 極限と級数が順序交換であるための条件|微分と級数の交換も解説
関数列{fₙ}の級数Σfₙについて,極限limや微分d/dxを計算するとき,Σとlimの順序交換,Σとd/dxの順序交換ができると簡単に計算が進むことはよくあります.この記事では,これらが交換可能であるための条件を解説します.
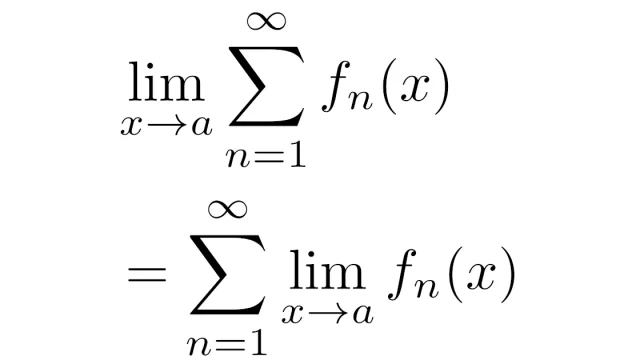 測度論
測度論 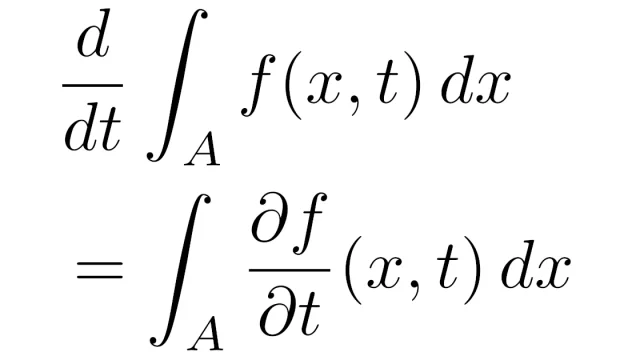 ルベーグ積分の基本
ルベーグ積分の基本  ルベーグ積分
ルベーグ積分 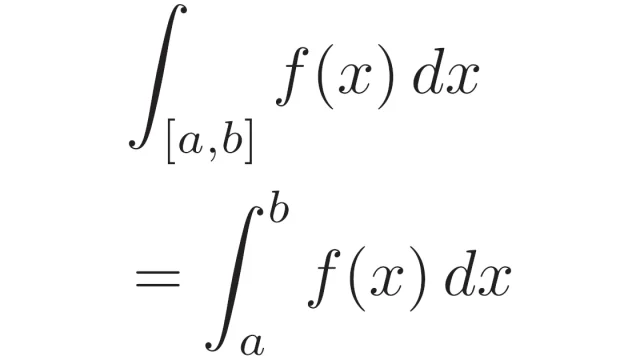 ルベーグ積分の基本
ルベーグ積分の基本 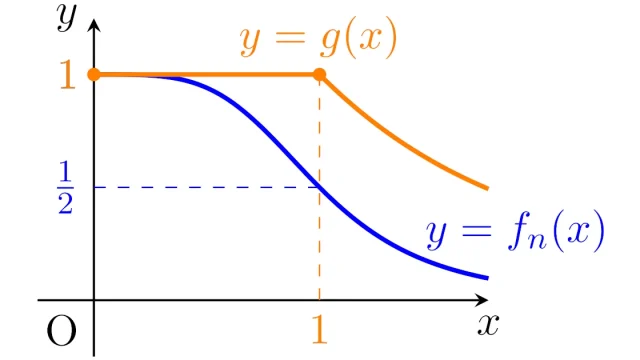 ルベーグ積分の基本
ルベーグ積分の基本 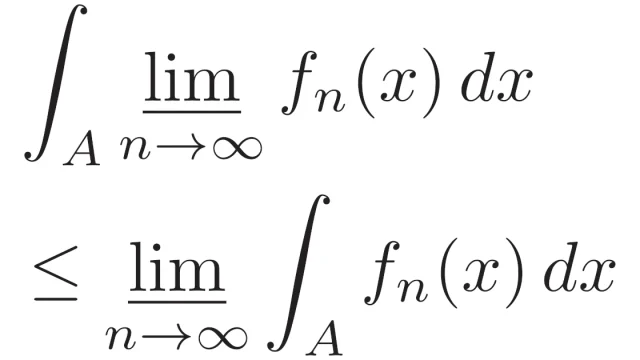 ルベーグ積分の基本
ルベーグ積分の基本 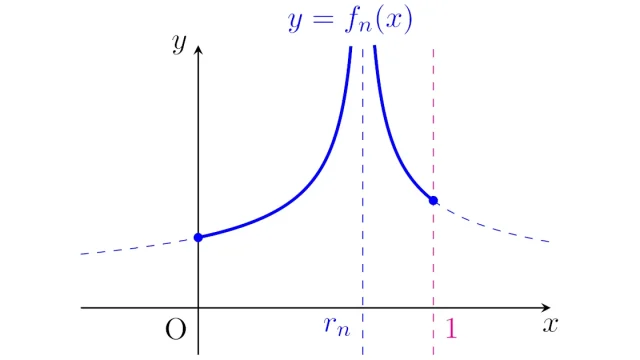 ルベーグ積分の基本
ルベーグ積分の基本 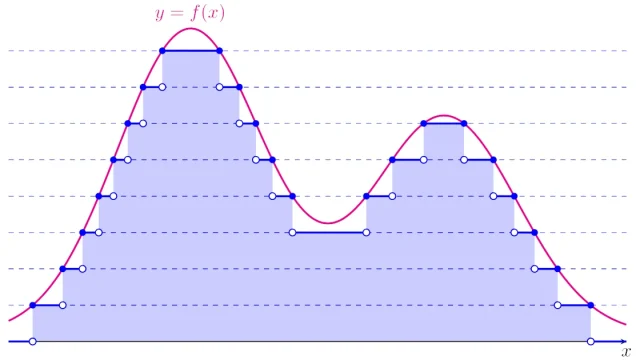 ルベーグ積分の基本
ルベーグ積分の基本 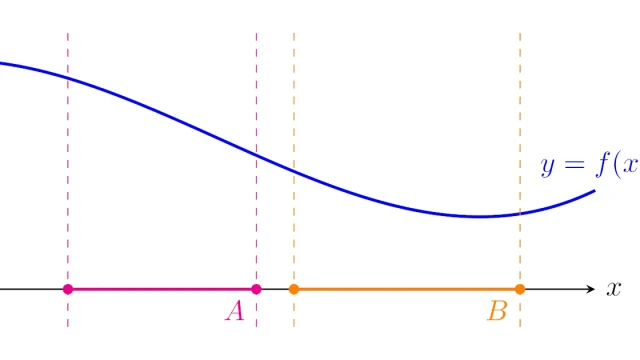 ルベーグ積分の基本
ルベーグ積分の基本 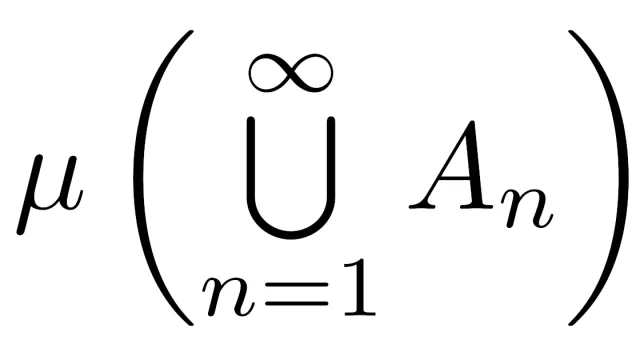 測度論
測度論