「可測関数列$\{f_n\}$が$0\le f_1\le f_2\le\dots$を満たすとき，項別積分
\begin{align*}\lim_{n\to\infty}\int_{A}f_n(x)\,dx=\int_{A}\lim_{n\to\infty}f_n(x)\,dx\end{align*}
が成り立つ」という定理をルベーグの単調収束定理というのでした．
しかし，ルベーグの単調収束定理が使えるには単調増加性$f_1\le f_2\le\dots$が必要なため，そのままではルベーグの単調収束定理が使えない場面も多くあります．
単調でない場合には非負値可測関数$\{f_n\}$に対して成り立つファトゥの補題というものがあり，ファトゥの補題はルベーグ積分の重要定理であるルベーグの収束定理を証明するために重要な役割を果たします．
また，$\lim\limits_{n\to\infty}\dint_{A}f_n(x)\,dx$の形の極限が正の無限大$\infty$に発散することを証明するために，ファトゥの補題が便利なことがあります．
この記事では
- 関数の下極限
- ファトゥの補題の証明と等号が成り立たない例
- ファトゥの補題を用いる発散の証明の例題
を順に解説します．
「ルベーグ積分の基本」の一連の記事
- ルベーグ積分入門
- ルベーグ測度
- ルベーグ可測関数とルベーグ積分
ルベーグ積分の参考文献
以下はルベーグ積分に関するオススメの教科書です．
ルベグ積分入門
ロングセラーの入門書です．専門書ですが，文庫なので安く購入できるのも魅力です．
ルベーグ積分と関数解析
ルベーグ積分から更なるステップに進みたい人向けの教科書です．
関数の下極限
ファトゥの補題のために関数列$\{f_n\}$の下極限$\liminf\limits_{n\to\infty}f_n$が必要となるので定義しておきましょう．
実数列の下極限
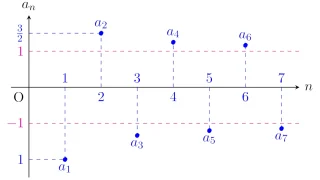
まずは実数列$\{a_n\}$の下極限$\liminf\limits_{n\to\infty}a_n$の定義を確認しておきましょう．
実数列$\{a_n\}$に対して，
\begin{align*}\liminf_{n\to\infty}a_n:=\lim_{n\to\infty}\Bigl(\inf_{p\ge n}a_p\Bigr)\end{align*}
を実数列$\{a_n\}$の下極限という．実数列$\{a_n\}$の下極限は$\varliminf\limits_{n\to\infty}a_n$と表すこともある．
言葉で説明すれば，「$\{a_n,a_{n+1},a_{n+2},\dots\}$の下限の$n\to\infty$の極限」が下極限$\liminf\limits_{n\to\infty}a_n$というわけですね．
実数列の（上極限と）下極限について詳しくは以下の記事を参照してください．
関数列の下極限
通常の関数列$\{f_n\}$の極限と同様に，定義域上の各点$x$に対して下極限を考えてできる関数が関数列$\{f_n\}$の下極限$\liminf\limits_{n\to\infty}f_n$です．
集合$A\subset\R$上の関数列$\{f_n\}$に対して，
\begin{align*}\Bigl(\liminf_{n\to\infty}f_n\Bigr)(x):=\lim_{n\to\infty}\Bigl(\inf_{p\ge n}f_p(x)\Bigr)\quad(x\in A)\end{align*}
で定まる$A$上の関数$\liminf\limits_{n\to\infty}f_n$を$\{f_n\}$の下極限という．実数値関数列$\{f_n\}$の下極限は$\varliminf\limits_{n\to\infty}f_n$と表すこともある．
右辺の$\lim\limits_{n\to\infty}\Bigl(\inf\limits_{p\ge n}f_p(x)\Bigr)$は$x$を止めるごとに決まる実数列$\Bigl\{\inf\limits_{p\ge n}f_n(x)\Bigr\}$の下極限です．この$\lim\limits_{n\to\infty}\Bigl(\inf\limits_{p\ge n}f_p(x)\Bigr)$を各$x$に対応させる関数が$\liminf\limits_{n\to\infty}f_n$というわけですね．
実数列の場合と同じく，$\inf$の代わりに$\sup$を考えて同様に関数列$\{f_n\}$の上極限$\limsup\limits_{n\to\infty}f_n$が定義され，
\begin{align*}\liminf\limits_{n\to\infty}f_n\le\limsup\limits_{n\to\infty}f_n\end{align*}
が成り立ちます．さらに定義域上の各点$x$で考えれば，実数列の場合と同様に次が成り立ちますね．
実数値関数列$\{f_n\}$に対して，次は同値である．
- $\liminf\limits_{n\to\infty}f_n=\limsup\limits_{n\to\infty}f_n$が（$\pm\infty$も許して）成り立つ
- 極限$\lim\limits_{n\to\infty}f_n$が（$\pm\infty$も許して）存在する
また，(1)または(2)の少なくとも一方が成り立つ（したがって両方が成り立つ）とき，
\begin{align*}\lim_{n\to\infty}f_n=\limsup_{n\to\infty}f_n=\liminf_{n\to\infty}f_n\end{align*}
が成り立つ．
ファトゥの補題と証明と等号が成り立たない例
本題のファトゥの補題(Fatou’s lemma)は以下の定理です．
[ファトゥの補題] 可測集合$A$上の非負値可測関数列$\{f_n\}$に対して，
\begin{align*}\int_{A}\liminf_{n\to\infty}f_n(x)\,dx\le\liminf_{n\to\infty}\int_{A}f_n(x)\,dx\end{align*}
が成り立つ．
「ファトゥの『補題』」という名前ですがとても重要な定理です．
証明
証明にはルベーグの単調収束定理を用います．
任意の$n\in\N$と$x\in A$に対して
\begin{align*}\{f_n(x),f_{n+1}(x),\dots\}\subset\{f_{n+1}(x),f_{n+2}(x),\dots\}\end{align*}
だから，$\inf\limits_{p\ge n}f_p(x)\le\inf\limits_{p\ge n+1}f_p(x)$が成り立つ．また，$\{f_n\}$は非負値可測関数列だから$\inf\limits_{p\ge n}f_p$は非負値可測関数である．
よって，ルベーグの単調収束定理と下限の定義を併せて
\begin{align*}\int_{A}\liminf_{n\to\infty}f_p(x)\,dx
&=\int_{A}\lim_{n\to\infty}\Bigl(\inf_{p\ge n}f_p(x)\Bigr)\,dx
\\&=\lim_{n\to\infty}\int_{A}\inf_{p\ge n}f_p(x)\,dx
\\&=\lim_{n\to\infty}\bra{\inf_{p\ge n}\int_{A}\inf_{p\ge n}f_p(x)\,dx}
\\&\le\liminf_{n\to\infty}\int_{A}f_n(x)\,dx\end{align*}
が成り立つ．ただし，最後の不等号では$\inf\limits_{p\ge n}f_p\le f_n$を用いた．
等号が成り立たない例
ファトゥの補題では
\begin{align*}\int_{A}\liminf_{n\to\infty}f_n(x)\,dx<\liminf_{n\to\infty}\int_{A}f_n(x)\,dx\end{align*}
と等号が成り立たないような関数列$\{f_n\}$が存在します．例えば，$\R$上で
\begin{align*}f_n(x)=\begin{cases}n^2x&(0\le x\le\frac{1}{n})\\-n^2x+2n&(\frac{1}{n}\le x\le\frac{2}{n})\\0&(\text{other})\end{cases}\end{align*}
と定めると，$f_n$のグラフはどんどん尖っていくグラフになります．
\begin{tikzpicture}
\def\xs{-0.5}\def\xl{1.5}\def\ys{-0.5}\def\yl{2.5}
\coordinate[label=below left:O](O) at (0,0); %原点
\coordinate(xs) at (\xs,0); %x軸最小
\coordinate(xl) at (\xl,0); %x軸最大
\coordinate(ys) at (0,\ys); %y軸最小
\coordinate(yl) at (0,\yl); %y軸最大
\draw[->,>=stealth,semithick](xs)–(xl) node[right]{$x$}; %x軸
\draw[->,>=stealth,semithick](ys)–(yl) node[left]{$y$}; %y軸
\draw[dashed,blue](1/2,0)node[below]{$\frac{2}{n}$}–(1/2,2)–(0,2)node[left]{$n$};
\draw[blue,thick](xs)–(O)–(1/2,2)–(1,0)–(xl);
\draw[blue]($(1/2,2)!0.5!(1,0)$)node[above right]{$y=f_{n}(x)$};
\draw[blue](1,0)node[below]{$\frac{1}{n}$};
\end{tikzpicture}
このとき，先に積分をすると三角形の部分の面積１となり，先に下極限をとると各点$x$で$\liminf\limits_{n\to\infty}f_n(x)=0$となるので
\begin{align*}&\liminf_{n\to\infty}\int_{A}f_n(x)\,dx=\liminf_{n\to\infty}1=1,
\\&\int_{A}\liminf_{n\to\infty}f_n(x)\,dx=\int_{A}\liminf_{n\to\infty}0\,dx=0\end{align*}
となりますね．よって，確かにこの関数列$\{f_n\}$は等号が成り立たない例になっています．
この他にも
\begin{align*}f_n(x)=\begin{cases}1&(n\le x\le n+1)\\0&(\text{other})\end{cases}\end{align*}
のような正方形が無限遠方に逃げていくような関数列も等号が成り立たない例として有名です．
\begin{tikzpicture}
\def\r{.06}\def\xs{-0.5}\def\xl{4}\def\ys{-0.5}\def\yl{1.5}
\coordinate[label=below left:O](O) at (0,0); %原点
\coordinate(xs) at (\xs,0); %x軸最小
\coordinate(xl) at (\xl,0); %x軸最大
\coordinate(ys) at (0,\ys); %y軸最小
\coordinate(yl) at (0,\yl); %y軸最大
\draw[->,>=stealth,semithick](xs)–(xl) node[below]{$x$}; %x軸
\draw[->,>=stealth,semithick](ys)–(yl) node[left]{$y$}; %y軸
\draw[dashed,blue](2,0)node[below]{$n$}–(2,1) (3,0)node[below]{$n+1$}–(3,1);
\draw[blue,very thick](xs)–(2,0) (2,1)–(3,1)node[above]{$y=f_n(x)$} (3,0)–(xl);
\fill[blue] (2,1)circle[radius=\r] (3,1)circle[radius=\r];
\filldraw[blue,semithick,fill=white] (2,0)circle[radius=\r] (3,0)circle[radius=\r];
\end{tikzpicture}
ファトゥの補題を用いる発散の証明の例題
ファトゥの補題は$\dint_{A}f_n(x)\,dx$が$n\to\infty$で$\infty$に発散することを証明する際に便利なことがあります．
\begin{align*}\lim_{n\to\infty}\int_{[0,\infty)}\frac{1}{(1+x^{1/n})(1+x)}\,dx.\end{align*}
任意の$x\in[0,\infty)$に対して，
\begin{align*}\lim_{n\to\infty}\frac{1}{(1+x^{1/n})(1+x)}=\frac{1}{(1+0)(1+x)}=\frac{1}{1+x}\end{align*}
だから，ファトゥの補題より
\begin{align*}&\liminf_{n\to\infty}\int_{[0,\infty)}\frac{1}{(1+x^{1/n})(1+x)}\,dx
\\&\ge\int_{[0,\infty)}\liminf_{n\to\infty}\frac{1}{(1+x^{1/n})(1+x)}\,dx
\\&=\int_{[0,\infty)}\lim_{n\to\infty}\frac{1}{(1+x^{1/n})(1+x)}\,dx
\\&=\int_{[0,\infty)}\frac{1}{1+x}\,dx
=\lim_{R\to\infty}[\log{(1+x)}]_{0}^{R}
\\&=\lim_{R\to\infty}\log{(1+R)}
=\infty\end{align*}
が成り立つ．一般に上極限は下極限以上だから
\begin{align*}&\limsup_{n\to\infty}\int_{[0,\infty)}\frac{1}{(1+x^{1/n})(1+x)}\,dx
\\&\ge\liminf_{n\to\infty}\int_{[0,\infty)}\frac{1}{(1+x^{1/n})(1+x)}\,dx
=\infty\end{align*}
も成り立つ．よって，上極限と下極限は$\infty$で一致したから極限が存在し，
\begin{align*}\lim_{n\to\infty}\int_{[0,\infty)}\frac{1}{(1+x^{1/n})(1+x)}\,dx=\infty\end{align*}
が従う．
普通の極限$\lim\limits_{n\to\infty}$は存在しないことがあるので，いきなり
\begin{align*}\lim_{n\to\infty}\int_{[0,\infty)}\frac{1}{(1+x^{1/n})(1+x)}\,dx\end{align*}
から考え始めるのは良くないことに注意しましょう．しかし，下極限（と上極限）はいつでも存在するのでしたから，
\begin{align*}\liminf_{n\to\infty}\int_{[0,\infty)}\frac{1}{(1+x^{1/n})(1+x)}\,dx\end{align*}
から考え始めるのは問題ありませんね．
また，下極限が正の無限大$\infty$に発散するときは，いまの議論と同様に極限も存在して正の無限大$\infty$に発散することは当たり前にしておきましょう．
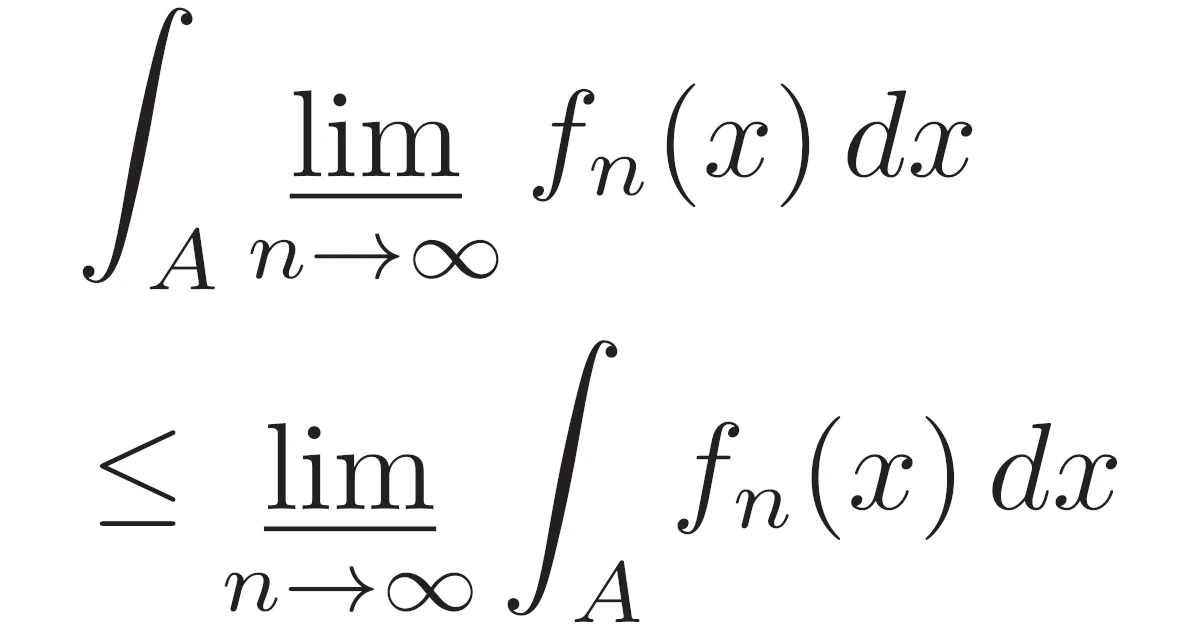
コメント