微分積分学で学ぶリーマン積分は定義域に注目する「縦切りの積分」である一方,ルベーグ積分は値域に注目する「横切りの積分」なのでした.
実は有界閉区間$[a,b]$上の有界関数$f$がリーマン積分可能なら,$f$は$[a,b]$上のルベーグ可積分関数であり,リーマン積分とルベーグ積分が等しくなることを証明することができます.
このため,有界閉区間においてルベーグ積分はリーマン積分の拡張であるということができます.
この記事では
- ルベーグ積分の計算の例題
- ルベーグ積分がリーマン積分の拡張であることの証明
を順に解説します.
「ルベーグ積分の基本」の一連の記事
- ルベーグ積分入門
- ルベーグ測度
- ルベーグ可測関数とルベーグ積分
ルベーグ積分の計算の例題
以下ではリーマン積分を$\dint_{a}^{b}$の形,ルベーグ積分を$\dint_{[a,b]}$の形で表して区別します.
冒頭でも触れたように,ルベーグ積分はリーマン積分の拡張となっていることが証明できます.
有界閉区間$[a,b]$上の有界関数$f$を考える.$f$が$[a,b]$上リーマン積分可能なら,$[a,b]$上ルベーグ積分可能で
\begin{align*}\int_{[a,b]}f(x)\,dx=\int_{a}^{b}f(x)\,dx\end{align*}
が成り立つ.
直接的には有界閉区間上の積分に関する定理になっていますが,うまく変形すれば有界閉区間でない場合にも使える場合があります(具体例2・具体例3を参照).
有界閉区間でない場合のリーマン積分は広義リーマン積分と呼ばれますね.広義リーマン積分可能であってもルベーグ積分可能でない関数が存在することには注意してください.
証明は後回しにして,まずは具体例から使い方を見てみましょう.
具体例1(有界閉区間上のルベーグ積分)
ルベーグ積分$\dint_{[0,1]}x^2\,dx$を求めよ.
$x^2$は$0\le x\le1$で有界である.リーマン積分$\dint_{0}^{1}x^2\,dx$は微分積分学の基本定理より
\begin{align*}\int_{0}^{1}x^2\,dx=\brc{\frac{1}{3}x^3}_{0}^{1}=\frac{1}{3}\end{align*}
と計算できる.よって,$[0,1]$上の$x^2$のルベーグ積分とリーマン積分は等しく,
\begin{align*}\int_{[0,1]}x^2\,dx=\frac{1}{3}\end{align*}
を得る.
具体例2(半開区間上のルベーグ積分)
ルベーグ積分$\dint_{(0,1]}\dfrac{1}{\sqrt{x}}\,dx$を求めよ.
この問題の積分は有界閉区間上ではないので上の定理をそのまま使うことはできませんが,定義関数$\mathbb{I}_{[\frac{1}{n},1]}$を用いて有界閉区間上の積分に持ち込みます.
$f(x):=\dfrac{1}{\sqrt{x}}$とおく.また,正の整数$n$に対して,有界閉区間$[\frac{1}{n},1]$で値1をとる定義関数を$\mathbb{I}_{[\frac{1}{n},1]}$とおく:
\begin{align*}\mathbb{I}_{[\frac{1}{n},1]}(x)=\begin{cases}1&(\frac{1}{n}\le x\le 1),\\0&(0<x<\frac{1}{n}).\end{cases}\end{align*}
一般に可測関数の積は可測関数だから,$f_n(x):=f(x)\mathbb{I}_{[\frac{1}{n},1]}(x)$で定まる関数$f_n:(0,1]\to\R$は可測関数である.
また,関数列$\{f_n\}$は各点$x\in(0,1]$において
\begin{align*}\lim_{n\to\infty}f_n(x)=\lim_{n\to\infty}f(x)\mathbb{I}_{[\frac{1}{n},1]}(x)=f(x)\end{align*}
と各点収束し,$f$が非負であることから$0\le f_1\le f_2\le\dots$が成り立つから,ルベーグの単調収束定理より
\begin{align*}\int_{(0,1]}f(x)\,dx
&=\lim_{n\to\infty}\int_{(0,1]}f_n(x)\,dx
\\&=\lim_{n\to\infty}\int_{[\frac{1}{n},1]}f(x)\,dx\end{align*}
が成り立つ.また,$[\frac{1}{n},1]$上の$f$のリーマン積分は
\begin{align*}\int_{\frac{1}{n}}^{1}f(x)\,dx=[2\sqrt{x}]_{\frac{1}{n}}^{1}=2-2\sqrt{\frac{1}{n}}\end{align*}
と計算できる.よって,$[\frac{1}{n},1]$上の$f$のルベーグ積分とリーマン積分は等しく,
\begin{align*}&\int_{(0,1]}\frac{1}{\sqrt{x}}\,dx
=\lim_{n\to\infty}\int_{[\frac{1}{n},1]}f(x)\,dx
\\&=\lim_{n\to\infty}\int_{\frac{1}{n}}^{1}f(x)\,dx
=\lim_{n\to\infty}\bra{2-2\sqrt{\frac{1}{n}}}
=2\end{align*}
を得る.
具体例3(無限区間上のルベーグ積分)
ルベーグ積分$\dint_{[0,\infty)}\dfrac{1}{1+x^2}\,dx$を求めよ.
この問題の積分も具体例2と同様に定義関数$\mathbb{I}_{[0,n]}$を用いて有界閉区間上の積分に持ち込みます.
$f(x):=\dfrac{1}{1+x^2}$とおく.また,正の整数$n$に対して,有界閉区間$[0,n]$で値1をとる定義関数を$\mathbb{I}_{[0,n]}$とおく:
\begin{align*}\mathbb{I}_{[0,n]}(x)=\begin{cases}1&(0\le x\le n),\\0&(n<x).\end{cases}\end{align*}
一般に可測関数の積は可測関数だから,$f_n(x):=f(x)\mathbb{I}_{[0,n]}(x)$で定まる関数$f_n:[0,\infty)\to\R$は可測関数である.
また,関数列$\{f_n\}$は各点$x\in[0,\infty)$において
\begin{align*}\lim_{n\to\infty}f_n(x)=\lim_{n\to\infty}f(x)\mathbb{I}_{[0,n]}=f(x)\end{align*}
と各点収束し,$f$が非負であることから$0\le f_1\le f_2\le\dots$が成り立つから,ルベーグの単調収束定理より
\begin{align*}\int_{[0,\infty]}f(x)\,dx
&=\lim_{n\to\infty}\int_{[0,\infty]}f_n(x)\,dx
\\&=\lim_{n\to\infty}\int_{[0,n]}f(x)\,dx\end{align*}
が成り立つ.また,$[0,n]$上の$f$のリーマン積分は
\begin{align*}\int_{0}^{n}f(x)\,dx=[\tan^{-1}{x}]_{0}^{n}=\tan^{-1}{n}\end{align*}
と計算できる.よって,$[0,n]$上の$f$のルベーグ積分とリーマン積分は等しく,
\begin{align*}&\int_{[0,\infty)}\frac{1}{1+x^2}\,dx
=\lim_{n\to\infty}\int_{[0,n]}f(x)\,dx
\\&=\lim_{n\to\infty}\int_{0}^{n}f(x)\,dx
=\lim_{n\to\infty}(\tan^{-1}{n})
=\frac{\pi}{4}\end{align*}
を得る.
ルベーグ積分がリーマン積分の拡張であることの証明
ルベーグ積分がリーマン積分の拡張となっていることを証明しましょう.
リーマン積分の上方和と下方和を用いた定義
ここでリーマン積分の定義を確認しておきましょう.
リーマン積分はリーマン和の極限として定義されることが多いですが,次のように上方和と下方和を用いて定義しても,リーマン和を用いた定義と同値です.
有界閉区間$[a,b]$上の有界関数$f$を考える.$[a,b]$の分割
\begin{align*}\Delta:a=x_0<x_1<x_2<\dots<x_n=b\end{align*}
に対して$I_k:=[x_{k-1},x_k]$とおく.
\begin{align*}M_k:=\sup_{x\in I_k}f(x),\quad
m_k:=\inf_{x\in I_k}f(x)\end{align*}
とし,$f$の$\Delta$に関する上方和(不足和)$S_{\Delta}$と下方和(過剰和)$s_{\Delta}$をそれぞれ
\begin{align*}S_{\Delta}:=\sum_{k=1}^{n}M_k|I_k|,\quad
s_{\Delta}:=\sum_{k=1}^{n}m_k|I_k|\end{align*}
と定める.さらに,区間の最大幅を$d_{\Delta}:=\max\limits_{k\in\{1,2,\dots,n\}}|I_k|$とおく.このとき,
\begin{align*}\lim_{d_{\Delta}\to0}S_{\Delta}=\lim_{d_{\Delta}\to0}s_{\Delta}\end{align*}
が成り立つとき,$f$は$[a,b]$上リーマン積分可能であるという.また,この極限をリーマン積分といい$\dint_{a}^{b}f(x)\,dx$と表す.
つまり,長方形近似の上限と下限が分割を細かくして同じ値に近付くとき,その値をリーマン積分というわけですね.
以下のルベーグ積分がリーマン積分の拡張となっていることの証明では,このリーマン積分の定義を採用しましょう.
定理の証明
それでは定理を証明しましょう.
(再掲)有界閉区間$[a,b]$上の有界関数$f$を考える.$f$が$[a,b]$上リーマン積分可能なら,$[a,b]$上ルベーグ積分可能で
\begin{align*}\int_{[a,b]}f(x)\,dx=\int_{a}^{b}f(x)\,dx\end{align*}
が成り立つ.
ステップ1(上方和・下方和とルベーグ積分)
有界閉区間$[a,b]$の均等な幅$\dfrac{b-a}{2^n}$への分割
\begin{align*}\Delta_n:a=x_0<x_1<x_2<\dots<x_{2^n}=b\end{align*}
を考え,$I_k:=[x_{k-1},x_k]$とおく.集合$X$上で値1をとる単関数を$\mathbb{I}_X$で表すとして,単関数$f_{n}^{+}$, $f_{n}^{-}$を
\begin{align*}&f_{n}^{+}=\sum_{k=1}^{n}M_k\mathbb{I}_{I_k},\quad
M_k:=\sup_{x\in I_k}f(x),
\\&f_{n}^{-}=\sum_{k=1}^{n}m_k\mathbb{I}_{I_k},\quad
m_k:=\inf_{x\in I_k}f(x)\end{align*}
と定める.一般に$\R$上の区間は可測集合だから,単関数の可測性の必要十分条件から$f_{n}^{+}$, $f_{n}^{-}$はともに可測関数である.
このとき,単関数のルベーグ積分の定義より$\dint_{[a,b]} f_{n}^{+}(x)\,dx$, $\dint_{[a,b]} f_{n}^{-}(x)\,dx$はそれぞれ$f$の$\Delta$に関する上方和・下方和となる.
$n\to\infty$とすると分割$\Delta_n$の小区間の幅は一様に0に近付くから,$f$が$[a,b]$上リーマン積分可能であることから
\begin{align*}\lim_{n\to\infty}\int_{[a,b]}f_{n}^{+}(x)\,dx=\lim_{n\to\infty}\int_{[a,b]} f_{n}^{-}(x)\,dx=\int_{a}^{b}f(x)\,dx\quad\dots(*)\end{align*}
が成り立つ.
ステップ2(ルベーグの収束定理)
(1) $\{f_{n}^{+}\}$は$n$に関して単調減少, $\{f_{n}^{-}\}$は$n$に関して単調増加である.
また,$f$が$[a,b]$上有界であることから,ある$M>0$が存在して,任意の$x\in[a,b]$に対して$|f(x)|\le M$が成り立つ.これより任意の$n$に対して
\begin{align*}|f_{n}^{\pm}(x)|\le M\quad(a\le x\le b)\quad\dots(**)\end{align*}
が成り立つ.
よって,$[a,b]$上の各点で単調有界実数列の収束定理を用いると,$\{f_{n}^{\pm}\}$の各点収束を得る.
(2) また,関数$g:=M\mathbb{I}_{[a,b]}$とすると,$(**)$より$[a,b]$上で$n$によらず
\begin{align*}|f_{n}^{\pm}(x)|\le g(x)\quad(a\le x\le b)\end{align*}
が成り立つ.
(3) 単関数のルベーグ積分の定義より
\begin{align*}\int_{[a,b]}g(x)\,dx=M m([a,b])=M(b-a)<\infty\end{align*}
なので$g$はルベーグ可積分関数である.ただし,$m$はルベーグ測度である.
(1)-(3)より,関数列$\{f_{n}^{\pm}\}$にルベーグの収束定理が適用できて
\begin{align*}\lim_{n\to\infty}\int_{[a,b]}f_{n}^{\pm}(x)\,dx=\int_{[a,b]}\lim_{n\to\infty}f_{n}^{\pm}(x)\,dx\end{align*}
が成り立つ(複号同順).
ステップ3(はさみうちの原理)
ステップ2と$(*)$のひとつ目の等号と併せて
\begin{align*}\int_{[a,b]}\Bigr(\lim_{n\to\infty}f_{n}^{+}-\lim_{n\to\infty}f_{n}^{-}\Bigl)(x)\,dx=0\end{align*}
となり,さらに$f_{n}^{+}-f_{n}^{-}$が非負関数であることと併せて,$[a,b]$上のほとんど至るところで$\lim\limits_{n\to\infty}f_{n}^{+}=\lim\limits_{n\to\infty}f_{n}^{-}$が従う.
また,任意の$n$に対して$f_{n}^{-}\le f\le f_{n}^{+}$だから,はさみうちの原理と併せて
\begin{align*}\lim_{n\to\infty}f_{n}^{+}=\bra{\lim_{n\to\infty}f_{n}^{-}=}f\end{align*}
がほとんど至るところで成り立つ.
以上より,
\begin{align*}&\int_{[a,b]}f(x)\,dx=\int_{[a,b]}\lim_{n\to\infty}f_{n}^{+}\,dx
\\&=\lim_{n\to\infty}\int_{[a,b]}f_{n}^{+}\,dx=\int_{a}^{b}f(x)\,dx\end{align*}
が従う.

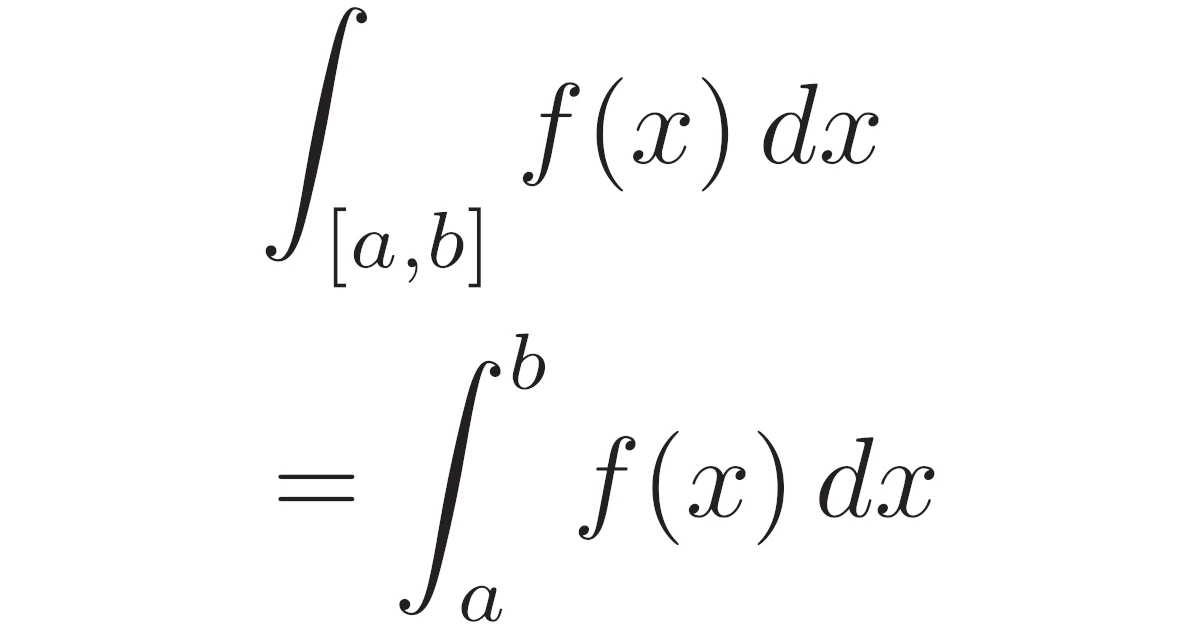


コメント