一般の線形空間$V$にはスカラー倍と和が定義されているので,いくつかのベクトルをもとにしてスカラー倍と和を用いて様々なベクトルを表すことができますね.
つまり,ベクトル$\m{v}_1,\m{v}_2,\dots,\m{v}_n\in V$とスカラー$c_1,c_2,\dots,c_n$によって
\begin{align*}c_1\m{v}_1+c_2\m{v}_2+\dots+c_n\m{v}_n\quad\dots(*)\end{align*}
と表せる$V$のベクトルを考えることができます.
このベクトル$(*)$を$\m{v}_1,\m{v}_2,\dots,\m{v}_n$の線形結合といい,線形空間においてよく用いられます.
また,この線形結合に関連した線形独立性も線形空間では重要な概念です.
この記事では
- 線形結合の定義と具体例
- 線形独立性の定義と具体例
を順に解説します.
なお,列ベクトルの線形空間$\R^n$の線形結合だけで十分なら,列ベクトルの線形結合に絞って解説した以下の記事の方が分かりやすいでしょう.
「線形空間の基本」の一連の記事
- 線形空間
- 線形写像
- 線形写像は行列の一般化!定義と具体例を解説(準備中)
- 線形写像は基底が命!基底との重要な関係(準備中)
- 線形写像の像Im(f)とKer(f)の定義と例題(準備中)
- 線形空間の同型の定義と次元定理を解説(準備中)
- 線形空間が同型と次元の超重要な関係(準備中)
線形結合の定義と具体例
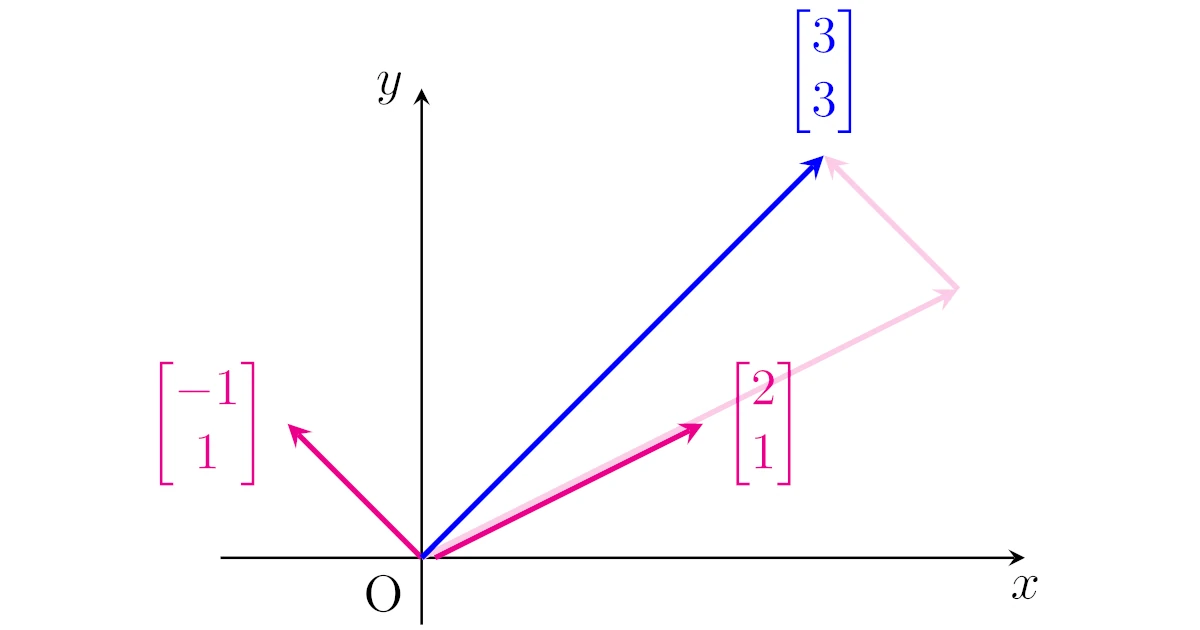
例えば,$\R^2$において
\begin{align*}2\bmat{2\\1}+1\bmat{-1\\1}=\bmat{3\\3}\end{align*}
は$\bmat{2\\1}$の2倍と$\bmat{-1\\1}$の1倍の和が$\bmat{3\\3}$になるという意味の式ですね.
このように「伸び縮み」させた2次列ベクトルたちの和で表す列ベクトルを$\R^2$における線形結合と言います.
線形結合の定義
一般の線形空間上の線形結合を次のように定義します.
体$\mathbb{F}$上の線形空間$V$に対して,$\m{v}_1,\m{v}_2,\dots,\m{v}_n\in V$の線形結合(linear combination)とは
\begin{align*}c_1\m{v}_1+c_2\m{v}_2+\dots+c_n\m{v}_n\quad(c_1,c_2,\dots,c_n\in\mathbb{F})\end{align*}
で表される$V$のベクトルのことをいう.
2次列ベクトルは上のように「(平行移動を許す)矢印」を用いて図示できました.
しかし,以下の具体例で考えるように,一般の線形空間は必ずしも図示できるわけではないことに注意しましょう.
具体例1(列ベクトルの線形空間$\R^4$上の線形結合)
$\R$上の4次列ベクトルの線形空間$\R^4$を考えます.このとき,$\bmat{1\\0\\1\\2},\bmat{0\\-2\\-1\\0},\bmat{1\\-1\\0\\-1}\in\R^4$の線形結合は
\begin{align*}c_1\bmat{1\\0\\1\\2}+c_2\bmat{0\\-2\\-1\\0}+c_3\bmat{1\\-1\\0\\-1}\quad(c_1,c_2,c_3\in\R)\end{align*}
と表されるベクトルのことですね.係数$c_1,c_2,c_3$はなんでも良いので,例えば
- $2\bmat{1\\0\\1\\2}+0\bmat{0\\-2\\-1\\0}+1\bmat{1\\-1\\0\\-1}=\bmat{3\\-1\\2\\3}$
- $1\bmat{1\\0\\1\\2}+2\bmat{0\\-2\\-1\\0}+(-1)\bmat{1\\-1\\0\\-1}=\bmat{0\\-3\\-1\\3}$
はいずれも$\bmat{1\\0\\1\\2},\bmat{0\\-2\\-1\\0},\bmat{1\\-1\\0\\-1}$の線形結合です.
4次列ベクトルを図示できなくても何も問題ありません.むしろ直接は「見え」なくても,式だけで処理できるのが数学のありがたいところです.
列ベクトルの線形結合の具体例については,以下の記事も参照してください.

具体例2(多項式の線形空間$\R[x]_2$上の線形結合)
$\R$上の2次以下の実数係数多項式全部の線形空間$\R[x]_2$を考えます.このとき,$1+x^2,2-2x\in\R[x]_2$の線形結合は
\begin{align*}c_1(1+x^2)+c_2(2-2x)\quad(c_1,c_2\in\R)\end{align*}
と表されるベクトルのことですね.係数$c_1,c_2$はなんでも良いので,例えば
- $1(1+x^2)+2(2-2x)=5-4x+x^2$
- $2(1+x^2)+(-3)(2-2x)=-4+6x+2x^2$
- $0(1+x^2)+2(2-2x)=4-4x$
- $0(1+x^2)+0(2-2x)=0$
はいずれも$1+x^2$, $2-2x$の線形結合です.
高校数学で学ぶように「矢印」のようなものでなくても,線形空間の元のことをベクトルというのでしたから,線形空間$\R[x]_2$の元は全てベクトルと呼ぶのでした.
具体例3(実数列の線形空間$\ell(\R)$上の線形結合)
$\R$上の実数列全部の線形空間$\ell(\R)$を考えます.このとき,一般項がそれぞれ$a_n=n$, $b_n=(-1)^n$の$\{a_n\},\{b_n\}\in\ell(\R)$の線形結合は
\begin{align*}c_1\{a_n\}+c_2\{b_n\}\quad(c_1,c_2\in\R)\end{align*}
と表されるベクトルのことですね.係数$c_1,c_2$はなんでも良いので,例えば
- $2\{a_n\}+1\{b_n\}=\{2n+(-1)^n\}=(1,5,5,9,\dots)$
- $1\{a_n\}+(-2)\{b_n\}=\{n-2(-1)^n\}=(-1,4,1,6,\dots)$
- $0\{a_n\}+0\{b_n\}=(0,0,0,0,\dots)$
はいずれも$\{a_n\}$, $\{b_n\}$の線形結合です.
線形独立性の定義と具体例
例えば,$\R^2$において
\begin{align*}c_1\bmat{2\\1}+c_2\bmat{-1\\1}=\bmat{0\\0}\end{align*}
という等式を考えると,第1成分・第2成分を比較して連立1次方程式を解けば$c_1=c_2=0$となりますね.
左辺は$\bmat{2\\1}$, $\bmat{-1\\1}$の線形結合ですから,「2次列ベクトル$\bmat{2\\1}$, $\bmat{-1\\1}$の線形結合で零ベクトル$\bmat{0\\0}$をつくるには係数を全て0にするしかない」ということができますね.
このことを$\bmat{2\\1}$, $\bmat{-1\\1}$は$\R^2$において線形独立であると言います.
直感的にはベクトルたちが完全にバラバラな方向を向いているときに線形独立となりますね.
線形関係の定義
一般の線形空間上の線形独立性を定義するために,まずは線形関係を定義しておきましょう.
体$\mathbb{F}$上の線形空間$V$に対して,$\m{v}_1,\m{v}_2,\dots,\m{v}_n\in V$の線形関係(linear combination)とは等式
\begin{align*}c_1\m{v}_1+c_2\m{v}_2+\dots+c_n\m{v}_n=\m{0}\quad(c_1,c_2,\dots,c_n\in\mathbb{F})\end{align*}
のことをいう.
つまり,ベクトル$\m{v}_1,\m{v}_2,\dots,\m{v}_n$の線形結合で零ベクトル$\m{0}$を表す等式を$\m{v}_1,\m{v}_2,\dots,\m{v}_n$の線形関係というわけですね.
どんなベクトルたち$\m{v}_1,\m{v}_2,\dots,\m{v}_n$に対しても,係数を全て0にすれば等式
\begin{align*}0\m{v}_1+0\m{v}_2+\dots+0\m{v}_n=\m{0}\end{align*}
が成り立ちますから,この線形関係を自明な線形関係といいます.
また,例えば$\bmat{1\\2},\bmat{-2\\-4}\in\R^2$に対しては,係数を全て0にしなくても等式
\begin{align*}2\bmat{1\\2}+(-1)\bmat{2\\4}=\bmat{0\\0}\end{align*}
が成り立ちますね.このようないずれかの係数が0でない線形関係を非自明な線形関係といいます.
線形独立性の定義
自明な線形結合はどんなベクトルたちに対しても存在しますが,非自明な線形結合が存在するかどうかはどんなベクトルたちを考えるかで変わります.
言い換えると,考えるベクトルたちによって,線形関係が自明なもののみであるかどうかが変わります.
そこで,一般の線形空間上の線形独立性を次のように定義します.
体$\mathbb{F}$上の線形空間$V$に対して,$\m{v}_1,\m{v}_2,\dots,\m{v}_n\in V$が線形独立(linearly independent)であるとは,$\m{v}_1,\m{v}_2,\dots,\m{v}_n$の線形関係が自明な線形関係に限ることをいう.
また,$\m{v}_1,\m{v}_2,\dots,\m{v}_n\in V$が線形独立でないことを,$\m{v}_1,\m{v}_2,\dots,\m{v}_n$は線形従属(linearly dependent)であるという.
いくつか具体例を考えましょう.
具体例1(列ベクトルの線形空間$\R^4$上の線形独立)
$\R$上の4次列ベクトルの線形空間$\R^4$において,$\m{a}_1:=\bmat{1\\0\\1\\2}$, $\m{a}_2:=\bmat{0\\-2\\-1\\0}$, $\m{a}_3:=\bmat{1\\-1\\0\\-1}$を考える.
このとき,$\m{a}_1,\m{a}_2,\m{a}_3$が線形独立であることを示せ.
$\m{a}_1,\m{a}_2,\m{a}_3$の線形関係
\begin{align*}c_1\bmat{1\\0\\1\\2}+c_2\bmat{0\\-2\\-1\\0}+c_3\bmat{1\\-1\\0\\-1}=\bmat{0\\0\\0\\0}\quad(c_1,c_2,c_3\in\R)\end{align*}
を考える.両辺で各成分を比較すれば
\begin{align*}\begin{cases}c_1+c_3=0\\-2c_2-c_3=0\\c_1-c_2=0\\2c_1-c_3=0\end{cases}\end{align*}
が成り立つ.この連立1次方程式を解いて$c_1=c_2=c_3=0$を得る.
よって,$\m{a}_1,\m{a}_2,\m{a}_3$の線形関係は自明な線形結合に限るから,$\m{a}_1,\m{a}_2,\m{a}_3$は線形独立である.
列ベクトルの線形独立・線形従属の具体例については,以下の記事も参照してください.

具体例2(多項式の線形空間$\R[x]_2$上の線形独立)
$\R$上の2次以下の実数係数多項式全部の線形空間$\R[x]_2$において,$f(x):=1+x^2$, $g(x):=2-2x$を考える.このとき,$f(x)$, $g(x)$が線形独立であることを示せ.
$f(x),g(x)$の線形関係
\begin{align*}c_1(1+x^2)+c_2(2-2x)=0\quad(c_1,c_2\in\R)\end{align*}
を考える.左辺を整理して係数比較すれば
\begin{align*}(c_1+2c_2)-2c_2x+c_1x^2=0
\iff\begin{cases}c_1+2c_2=0\\-2c_2=0\\c_1=0\end{cases}\end{align*}
が成り立つ.この連立1次方程式を解いて$c_1=c_2=0$を得る.
よって,$f(x)$, $g(x)$の線形関係は自明な線形結合に限るから,$f(x)$, $g(x)$は線形独立である.
具体例3(多項式の線形空間$\R[x]_2$上の線形従属)
$\R$上の2次以下の実数係数多項式全部の線形空間$\R[x]_2$において,$f(x):=1+x^2$, $g(x):=2+x^2$を考える.このとき,$f(x)$, $g(x)$が線形独立でないことを示せ.
$f(x),g(x)$の線形関係
\begin{align*}c_1(1+x^2)+c_2(2+x^2)=0\quad(c_1,c_2\in\R)\end{align*}
を考える.左辺を整理して係数比較すれば
\begin{align*}(c_1+2c_2)+(c_1+c_2)x^2=0
&\iff\begin{cases}c_1+2c_2=0\\c_1+c_2=0\end{cases}\end{align*}
が成り立つ.この連立1次方程式を解いて$c_1=c_2=0$を得る.
よって,$f(x)$, $g(x)$の非自明な線形結合が存在したから,$f(x)$, $g(x)$は線形従属である.
慣れれば見た瞬間に$1+x^2$を2倍すれば$2+2x^2$となることが見てとれるので,すぐに線形従属であることが分かるようになってきます.
具体例4(実数列の線形部分空間上の線形独立)
$\R$上の実数列全部の線形空間$\ell(\R)$の線形部分空間
\begin{align*}V:=\set{\{a_n\}\in\ell(\R)}{a_{n+2}+a_{n+1}+a_{n}=0}\end{align*}
において,
\begin{align*}&\{a_n\}=(1,2,3,5,8,13,21,\dots),
\\&\{b_n\}=(2,-1,1,0,1,1,2,\dots)\end{align*}
を考える.このとき,$\{a_n\}$, $\{b_n\}$が線形独立であることを示せ.
漸化式$a_{n+2}+a_{n+1}+a_{n}=0$をみたす実数列$\{a_n\}$全部の線形部分空間が$V$ですね.
$\{a_n\},\{b_n\}\in V$の線形関係
\begin{align*}c_1\{a_n\}+c_2\{b_n\}=(0,0,0,\dots)\quad(c_1,c_2\in\R)\end{align*}
を考える.左辺を整理して第1項と第2項を比較すれば
\begin{align*}&\{c_1a_n+c_2b_n\}=(0,0,0,\dots)
\\&(c_1+2c_2,2c_1-c_2,3c_1+c_2,\dots)=(0,0,0,\dots)
\\&\iff\begin{cases}c_1+2c_2=0\\2c_1-c_2=0\end{cases}\end{align*}
が成り立つ.この連立1次方程式を解いて$c_1=c_2=0$を得る.
よって,$\{a_n\}$, $\{b_n\}$の線形関係は自明な線形結合に限るから,$\{a_n\}$, $\{b_n\}$は線形独立である.

コメント