ガンマ分布$\mrm{Ga}(\alpha,\beta)$はガンマ関数をベースとした確率分布で,指数分布$\mrm{Ex}(\lambda)$やカイ二乗分布$\chi^2(n)$の一般化とも捉えられる重要な確率分布です.
ガンマ分布は
- 再生性
- 尺度変換を施してもガンマ分布
などの性質をもっており,ガンマ関数に従う確率変数の和や定数倍がどのような分布に従うか簡単に分かる場合も多いです.
また,ガンマ分布に従う独立な2つの確率変数から,ベータ分布に従う確率変数を作ることもできます.
この記事では
- ガンマ分布の再生性と尺度変換
- ガンマ分布と指数分布・$\chi^2$分布の関係
- ガンマ分布とベータ分布の関係
を順に説明します.
ガンマ分布の定義・尺度変換・再生性
まずはガンマ分布の定義を確認し,ガンマ分布に関する再生性と尺度変換を考えましょう.
ガンマ分布の定義($X\sim\mrm{Ga}(\alpha,\beta)$)
$\alpha>0$, $\beta>0$とする.実数値確率変数$X$がガンマ分布(gamma distribution)に従うとは,$X$の確率密度関数が
\begin{align*}f_X(x)=\frac{1}{\Gamma(\alpha)\beta^\alpha}x^{\alpha-1}e^{-x/\beta}\quad(x>0)\end{align*}
であることをいい,このとき$X\sim\mrm{Ga}(\alpha,\beta)$と表す.また,$\alpha$を形状母数(shape parameter),$\beta$を尺度母数(scale parameter)という.
ただし,$\Gamma$はガンマ関数である:
\begin{align*}\Gamma(\alpha)=\int_{0}^{\infty}x^{\alpha-1}e^{-x}\,dx.\end{align*}
ガンマ分布は$\beta=1$のときをもとにして考えると捉えやすいです.$X\sim\mrm{Ga}(\alpha,1)$なら
\begin{align*}f_X(x)=\frac{1}{\Gamma(\alpha)}x^{\alpha-1}e^{-x}\end{align*}
となり,後ろの$x^{\alpha-1}e^{-x}$はガンマ関数の被積分関数ですから,前の$\frac{1}{\Gamma(\alpha)}$はただの正規化定数になっているだけですね.
ここから$X$を$\beta$倍する尺度変換を用いることで,$X\sim\mrm{Ga}(\alpha,\beta)$なら
\begin{align*}f_X(x)=\frac{1}{\Gamma(\alpha)\beta^\alpha}x^{\alpha-1}e^{-x/\beta}\quad(x>0)\end{align*}
となることが分かります.
尺度変換($kX\sim\mrm{Ga}(\alpha,k\beta)$)
一般に,確率変数$X$に対して,$Y=kX$の形の変換を尺度変換といいますね.
ガンマ分布に従う確率変数は尺度変換を施しても再びガンマ分布に従います.
$k>0$とする.$X\sim\mrm{Ga}(\alpha,\beta)$に対して,$kX\sim\mrm{Ga}(\alpha,k\beta)$が成り立つ.
このように尺度変換では$\mrm{Ga}(\alpha,\beta)$の第2パラメータの$\beta$だけが変化します.このことから$\beta$は尺度母数と呼ばれるわけですね.
累積分布関数の定義から
\begin{align*}F_Y(y)=P(Y\le y)=P(kX\le y)=P\bra{X\le\frac{y}{k}}=F_X\bra{\frac{y}{k}}\end{align*}
なので,両辺を$y$で微分して
\begin{align*}f_Y(y)&=f_X\bra{\frac{y}{k}}\cdot\frac{1}{k}
\\&=\frac{1}{\Gamma(\alpha)\beta^\alpha}\bra{\frac{x}{k}}^{\alpha-1}e^{-x/k\beta}\cdot\frac{1}{k}
\\&=\frac{1}{\Gamma(\alpha)(k\beta)^\alpha}x^{\alpha-1}e^{-x/k\beta}\end{align*}
を得る.よって,$kX\sim\mrm{Ga}(\alpha,k\beta)$が成り立つ.
確率変数の変換公式$f_Y(y)=f_X(g^{-1})/|g'(g^{-1}(y))|$にそのまま代入しても得られます(公式の証明と同様の議論をガンマ分布でしただけです).
再生性($X+Y\sim\mrm{Ga}(\alpha_1+\alpha_2,\beta)$)
一般に,同じ種類の確率分布に従う独立な確率変数$X$, $Y$の和$X+Y$がもとと同じ種類の確率分布に従うとき,その性質を確率分布の再生性といいますね.
尺度母数が等しい2つのガンマ分布に従う独立な確率変数$X$, $Y$の和$X+Y$も,再びガンマ分布に従います.
独立な$X\sim\mrm{Ga}(\alpha_1,\beta)$, $Y\sim\mrm{Ga}(\alpha_2,\beta)$に対して,$X+Y\sim\mrm{Ga}(\alpha_1+\alpha_2,\beta)$が成り立つ.
このように尺度母数が等しいときに再生性が成り立ち,尺度母数はそのままで形状母数はもとの2つの形状母数の和となります.
形状母数$\alpha$,尺度母数$\beta$のガンマ分布の積率母関数が$\frac{1}{(1-\beta t)^\alpha}$であることは認めて証明しましょう.
$X$, $Y$それぞれの積率母関数$M_X(t)$, $M_Y(t)$は
\begin{align*}M_X(t)=E[e^{tX}]=\frac{1}{(1-\beta t)^{\alpha_1}},\quad
M_Y(t)=E[e^{tY}]=\frac{1}{(1-\beta t)^{\alpha_2}}\end{align*}
である.$X$, $Y$は独立なので$e^{tX}$, $e^{tY}$も独立だから,$X+Y$の積率母関数$M_{X+Y}(t)$は
\begin{align*}M_{X+Y}(t)&=E[e^{t(X+Y)}]=E[e^{tX}e^{tY}]=E[e^{tX}]E[e^{tY}]
\\&=\frac{1}{(1-\beta t)^{\alpha_1}}\cdot\frac{1}{(1-\beta t)^{\alpha_2}}
=\frac{1}{(1-\beta t)^{\alpha_1+\beta_2}}\end{align*}
を得る.これは形状母数$\alpha_1+\alpha_2$,尺度母数$\beta$のガンマ分布の積率母関数だから,
\begin{align*}X+Y\sim\mrm{Ga}(\alpha_1+\alpha_2,\beta)\end{align*}
が成り立つ.
一般に独立な確率変数$X_1$, $X_2$に対し$E[X_1X_2]=E[X_1]E[X_2]$が成り立つことを利用して,$X+Y$の積率母関数を$X$, $Y$の積率母関数の積に表す部分が重要です.
これは積率母関数を用いた再生性の基本的な示し方なので,覚えておきたい方法です.
ガンマ分布と指数分布・$\chi^2$分布の関係
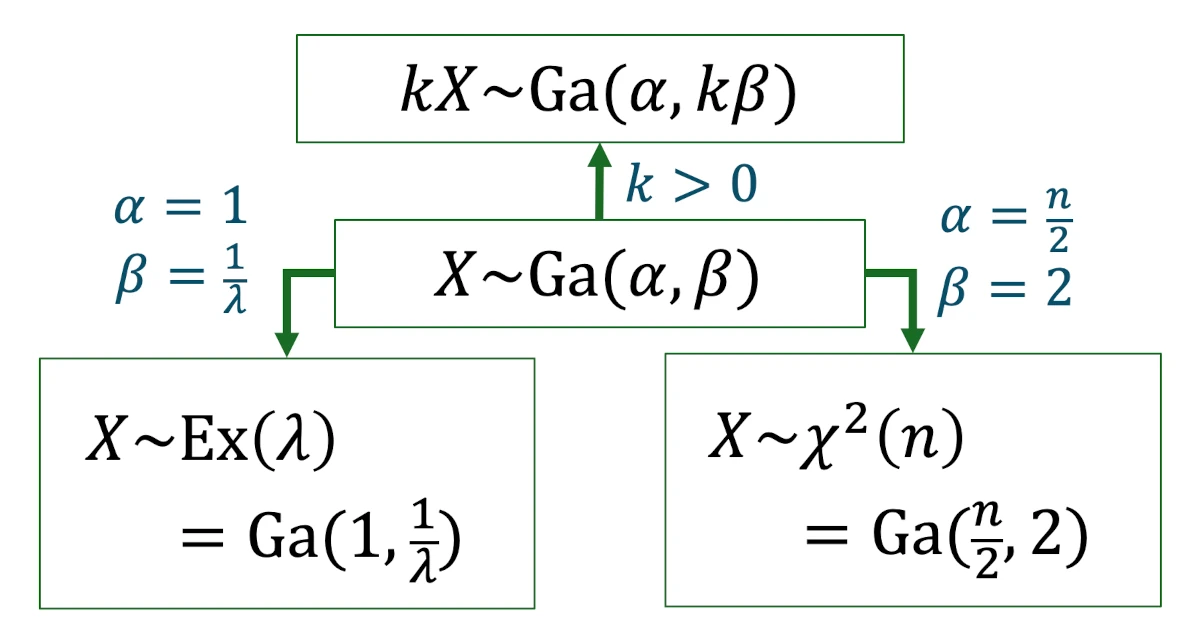
ガンマ分布は形状母数$\alpha$と尺度母数$\beta$を用いて$\mrm{Ga}(\alpha,\beta)$と表され,指数分布とカイ二乗分布はこれら2つのパラメータ$\alpha$, $\beta$を特別な値にとることで得られます.
上述のようにガンマ分布は確率変数の線形変換に対して良い性質を持ちますから,指数分布やカイ二乗分布をあえてガンマ分布と考えることで上手くいくこともあります.
指数分布は再生性を持ちませんし,カイ二乗分布に従う確率変数の定数倍は一般にはカイ二乗分布に従いません.
指数分布($\mrm{Ex}(\lambda)=\mrm{Ga}(1,\frac{1}{\lambda})$)
$\lambda>0$とする.実数値確率変数$X$が指数分布(exponential distribution)に従うとは,$X$の確率密度関数が
\begin{align*}f_X(x)=\lambda e^{-\lambda x}\quad(x>0)\end{align*}
であることをいい,このとき$X\sim\mrm{Ex}(\lambda)$と表す.
$X\sim\mrm{Ga}(\alpha,\beta)$の確率密度関数
\begin{align*}f_X(x)=\frac{1}{\Gamma(\alpha)\beta^\alpha}x^{\alpha-1}e^{-x/\beta}\end{align*}
と比較して,$\mrm{Ex}(\lambda)=\mrm{Ga}(1,\frac{1}{\lambda})$と分かります.
正の整数$n$に対して$\Gamma(n)=(n-1)!$でしたから,$\Gamma(1)=0!=1$ですね.
ガンマ分布の尺度変換に関する性質と併せて,次が成り立ちますね.
$\lambda>0$, $k>0$とする.$X\sim\mrm{Ex}(\lambda)$に対して,$kX\sim\mrm{Ex}\bra{\dfrac{\lambda}{k}}$が成り立つ.
$X\sim\mrm{Ex}(\lambda)=\mrm{Ga}(1,\frac{1}{\lambda})$だから,ガンマ分布の尺度変換に関する性質より
\begin{align*}kX\sim\mrm{Ga}\bra{1,k\cdot\frac{1}{\lambda}}=\mrm{Ga}\bra{1,\frac{1}{\lambda/k}}=\mrm{Ex}\bra{\frac{\lambda}{k}}\end{align*}
が成り立つ.
$\chi^2$分布($\chi^2(n)=\mrm{Ga}(\frac{n}{2},2)$)
$n$を正の整数とする.実数値確率変数$X$がカイ二乗分布(chi-squared distribution)に従うとは,$X$の確率密度関数が
\begin{align*}f_X(x)=\frac{1}{\Gamma(\frac{n}{2})2^{n/2}}x^{\frac{n}{2}-1}e^{-x/2}\quad(x>0)\end{align*}
であることをいい,このとき$X\sim\chi^2(n)$と表す.また,$n$を自由度という.
$X\sim\mrm{Ga}(\alpha,\beta)$の確率密度関数
\begin{align*}f_X(x)=\frac{1}{\Gamma(\alpha)\beta^\alpha}x^{\alpha-1}e^{-x/\beta}\end{align*}
と比較して,$\chi^2(n)=\mrm{Ga}(\frac{n}{2},2)$と分かります.
正の整数$n$に対して$\Gamma(n)=(n-1)!$でしたから,$\Gamma(1)=0!=1$ですね.
カイ二乗分布ではガンマ分布の尺度母数が常に2ですから,ガンマ分布の再生性が使えて次が成り立ちます.
$m$, $n$を正の整数とする.独立な$X\sim\chi^2(m)$, $Y\sim\chi^2(n)$に対して,$X+Y\sim\chi^2(m+n)$が成り立つ.
$X\sim\chi^2(m)=\mrm{Ga}(\frac{m}{2},2)$, $Y\sim\chi^2(n)=\mrm{Ga}(\frac{n}{2},2)$だから,ガンマ分布の再生性より
\begin{align*}X+Y\sim\mrm{Ga}\bra{\frac{m}{2}+\frac{n}{2},2}=\mrm{Ga}\bra{\frac{m+n}{2},2}=\chi^2(m+n)\end{align*}
が成り立つ.
ガンマ分布とベータ分布の関係
独立な2つの確率変数$X$, $Y$が尺度母数1のガンマ分布に従うとき,これらを用いてベータ分布に従う確率変数を作ることができます.
$a,b>0$とする.独立な$X\sim\mrm{Ga}(a,1)$, $Y\sim\mrm{Ga}(b,1)$に対して,$\dfrac{X}{X+Y}\sim\mrm{Beta}(a,b)$が成り立つ.
$Z\sim\mrm{Beta}(a,b)$の確率密度関数が
\begin{align*}f_Z(z)=\frac{1}{B(a,b)}z^{a-1}(1-z)^{b-1}\quad(0<x<1)\end{align*}
であることは認めて証明しましょう($B(a,b)$はベータ関数).
$X\sim\mrm{Ga}(a,1)$, $Y\sim\mrm{Ga}(b,1)$の確率密度関数はそれぞれ
\begin{align*}f_X(x)=\frac{1}{\Gamma(a)}x^{a-1}e^{-x},\quad
f_Y(y)=\frac{1}{\Gamma(b)}y^{b-1}e^{-y}\end{align*}
である.
変数変換$(X,Y)\to(Z,W)$
$Z=\frac{X}{X+Y}$, $W=X+Y$とおくと,$X=ZW$, $Y=(1-Z)W$なので,$(X,Y)$と$(Z,W)$は
- $\set{(x,y)\in\R^2}{x>0,y>0}$
- $\set{(z,w)\in\R^2}{0<z<1, w>0}$
で1対1に対応する.
$x=zw$, $y=(1-z)w$のヤコビアンは
\begin{align*}\det{\frac{\partial(x,y)}{\partial(z,w)}}&=\det\bmat{w&z\\-w&1-z}
\\&=w(1-z)-z(-w)=w\end{align*}
である.
$(Z,W)$の同時確率密度関数
$X$, $Y$は独立だから$f_{X,Y}(zw,(1-z)w)=f_{X}(zw)f_{Y}((1-z)w)$なので,$(Z,W)$の同時確率密度関数$f_{Z,W}$は
\begin{align*}f_{Z,W}(z,w)&=f_{X,Y}(zw,(1-z)w)\abs{\det{\frac{\partial(x,y)}{\partial(z,w)}}}
\\&=f_{X}(zw)f_{Y}((1-z)w)|w|
\\&=\frac{1}{\Gamma(a)}(zw)^{a-1}e^{-zw}\cdot\frac{1}{\Gamma(b)}((1-z)w)^{b-1}e^{-(1-z)w}\cdot w
\\&=\frac{1}{\Gamma(a)\Gamma(b)}z^{a-1}(1-z)^{b-1}w^{a+b-1}e^{-w}\end{align*}
である.これは($z$の関数)×($w$の関数)の形なので,$z$と$w$は独立で
\begin{align*}f_Z(z)=Cz^{a-1}(1-z)^{b-1},\quad
f_W(w)=C’w^{a+b-1}e^{-w}\end{align*}
の形となる($C$, $C’$は正規化定数).よって,$Z\sim\mrm{Beta}(a,b)$, $W\sim\mrm{Ga}(a+b,1)$が従う.
なお,このことから正規化定数は$C=\frac{1}{B(a,b)}$, $C’=\frac{1}{G(a+b)}$である.
一般に,$(X_1,X_2,\dots,X_n)$の同時確率密度関数$f_{X_1,X_2,\dots,X_n}(x_1,x_2,\dots,x_n)$が
\begin{align*}f_1(x_1)\times f_2(x_2)\times\dots\times f_n(x_n)\end{align*}
の形になるとき,$X_1,X_2,\dots,X_n$は独立で,$X_k$の確率密度関数が$f_k$であることが従います.
このことを使うために,$f_{Z,W}(z,w)$の確率密度関数を($z$の関数)×($w$の関数)の形に変形しました.
参考文献
以下は参考文献です.
現代数理統計学の基礎
[久保川達也 著/共立出版]
現代の統計学は社会学・心理学・機械学習など様々な分野に応用されている極めて実学的な分野です.
本書は本格的な統計学の基礎から,近年広く応用されている統計手法を学ぶことができるテキストで,
- 第1部:統計的推測を行う上で必要な確率・確率分布の基本的な事項
- 第2部:確率分布に関する推測方法
- 第3部:発展的な内容
の3部構成になっています(本書「はしがき」より).
著者が大学3,4年生に向けて行った講義に基づいて書かれており,全体的に簡潔に説明されているのが特徴です.
また,章末問題も豊富にあり,統計検定の準1級・1級の対策としても利用できます(たとえば,統計検定1級の「数理統計」は本書の第5章までをしっかり学べば十分対応できます).
さらに,著者による章末問題の略解がウェブにアップロードされているのも独学者にはありがたい点です.


コメント