正の整数$n$の階乗$n!$とは,$n$以下の全ての正の整数の積のことをいうのでした.例えば,
\begin{align*}5!=5\times4\times3\times2\times1\end{align*}
ですね.実はガンマ関数という関数があり,このガンマ関数は階乗の実数(複素数)への拡張としてよく知られています.
ガンマはギリシャ文字の$\Gamma$のことで,$\Gamma$関数と書くこともあります.なお,$\Gamma$の小文字は$\gamma$です.
ガンマ関数は微分積分学だけでなく,統計学や複素解析においても現れる重要な関数です.
この記事では
- ガンマ関数の定義と具体例
- ガンマ関数の基本性質
- ガンマ関数とベータ関数との関係
を順に説明します.
ガンマ関数の定義と具体例
まずはガンマ関数$\Gamma$を定義し,具体的に$\Gamma(1)$, $\Gamma(\frac{1}{2})$を求めましょう.
ガンマ関数の定義
正の実数$x$に対して
\begin{align*}\Gamma(x)=\int_{0}^{\infty}t^{x-1}e^{-t}\,dt\end{align*}
で定まる実数値関数$\Gamma$をガンマ関数(gamma function)という.
広義積分$\int_{0}^{\infty}t^{x-1}e^{-t}\,dt$が$x>0$のとき収束し,$x\le0$のとき発散することは,この記事の最後に証明しています.
ガンマ関数は実部が正の複素数に対しても同様に定義できますが,この記事では主に実数の場合を説明します.
具体的に$\Gamma(1)$, $\Gamma(\frac{1}{2})$を求めてみましょう.
具体例1($\Gamma(1)=1$)
$\Gamma(1)$はガンマ関数の定義より
\begin{align*}\Gamma(1)&=\int_{0}^{\infty}t^{1-1}e^{-t}\,dt=\int_{0}^{\infty}e^{-t}\,dt
\\&=[-e^{-t}]_{0}^{\infty}=-0+e^{-0}=1\end{align*}
となりますね.
のちに説明するように,0以上の整数$n$に対して$\Gamma(n+1)=n!$が成り立つので,この$\Gamma(1)=1$は$0!=1$ということに相当します.
具体例2($\Gamma(1/2)=\sqrt{\pi}$)
$\Gamma(\frac{1}{2})$はガンマ関数の定義より
\begin{align*}\Gamma\bra{\frac{1}{2}}=\int_{0}^{\infty}t^{\frac{1}{2}-1}e^{-t}\,dt=\int_{0}^{\infty}\frac{1}{\sqrt{t}}e^{-t}\,dt\end{align*}
となりますね.$s=\sqrt{t}$とおくと,$\frac{ds}{dt}=\frac{1}{2\sqrt{t}}$であり,$t$が$0$から$\infty$を動くとき$s$も$0$から$\infty$を動くので,
\begin{align*}\Gamma\bra{\frac{1}{2}}
=2\int_{0}^{\infty}e^{-s^2}\,ds
=\int_{-\infty}^{\infty}e^{-s^2}\,ds\end{align*}
が成り立ちます.最後の積分はガウス積分で$\sqrt{\pi}$に収束するので,$\Gamma(\frac{1}{2})=\sqrt{\pi}$と分かります.
このように$\Gamma(\frac{1}{2})$はガウス積分に帰着できて値が$\sqrt{\pi}$であることは知っておいて良いでしょう.
ガンマ関数の性質
ガンマ関数の基本性質を解説します.
ガンマ関数の別の表し方
ガンマ関数は以下のように表すこともできます.
正の実数$x$に対して
\begin{align*}\Gamma(x)=2\int_{0}^{\infty}s^{2x-1}e^{-s^2}\,ds\end{align*}
が成り立つ.
これは先ほど求めた$\Gamma(\frac{1}{2})$の計算のように置換することで得られます.
ガンマ関数の定義$\Gamma(x)=\dint_{0}^{\infty}t^{x-1}e^{-t}\,dt$に対して,$s=\sqrt{t}$とおくと,
\begin{align*}\frac{ds}{dt}=\frac{1}{2\sqrt{t}}\iff 2s\frac{ds}{dt}=1\end{align*}
であり,$t$が$0$から$\infty$を動くとき$s$も$0$から$\infty$を動くから,
\begin{align*}\Gamma(x)=\int_{0}^{\infty}(s^2)^{x-1}e^{-s^2}(2s\,ds)=2\int_{0}^{\infty}s^{2x-1}e^{-s^2}\,ds\end{align*}
が成り立つ.
$\Gamma(x+1)$と$\Gamma(x)$の関係
冒頭でも説明したように,ガンマ関数は階乗の一般化と捉えることができます.このことを示すために重要な性質を証明しましょう.
正の実数$x$に対して
\begin{align*}\Gamma(x+1)=x\Gamma(x)\end{align*}
が成り立つ.
ガンマ関数の定義と部分積分により
\begin{align*}\Gamma(x+1)
&=\int_{0}^{\infty}t^{(x+1)-1}e^{-t}\,dt
=\int_{0}^{\infty}t^{x}e^{-t}\,dt
\\&=\brc{-t^{x}e^{-t}}_{0}^{\infty}-\int_{0}^{\infty}\bra{-xt^{x-1}e^{-t}}\,dt
\\=&0+x\int_{0}^{\infty}t^{x-1}e^{-t}\,dt
=x\Gamma(x)\end{align*}
が成り立つ.
この命題を用いて,具体的に$\Gamma(5)$, $\Gamma(\frac{5}{2})$を求めてみましょう.
具体例3($\Gamma(5)$)
$\Gamma(5)$は
\begin{align*}\Gamma(5)&=4\Gamma(4)=4\cdot3\Gamma(3)=4\cdot3\cdot2\Gamma(2)
\\&=4\cdot3\cdot2\cdot1\Gamma(1)=4!\cdot\Gamma(1)\end{align*}
となって,具体例1で計算した$\Gamma(1)=1$より$\Gamma(5)=4!$と分かります.
このように,$\Gamma(1)=1$を当たり前にしておけば,帰納的に考えればガンマ関数の正の整数での値は簡単に求められますね.
具体例4($\Gamma(5/2)$)
$\Gamma(\frac{5}{2})$は
\begin{align*}\Gamma\bra{\frac{5}{2}}=\frac{3}{2}\Gamma\bra{\frac{3}{2}}
=\frac{3}{2}\cdot\frac{1}{2}\Gamma\bra{\frac{1}{2}}
=\frac{3\cdot1}{2^2}\Gamma\bra{\frac{1}{2}}\end{align*}
となって,具体例2で計算した$\Gamma(\frac{1}{2})=\sqrt{\pi}$より$\Gamma(\frac{5}{2})=\frac{3\cdot1}{2^2}\sqrt{\pi}$と分かります.
$\Gamma(5)$の計算と同様に,$\Gamma(\frac{1}{2})=\sqrt{\pi}$を当たり前にしておけば,帰納的に考えればガンマ関数の正の半整数での値は簡単に求められますね.
ガンマ関数と階乗の関係
具体例3の$\Gamma(5)=4!$を一般化すると次のようになりますね.
正の整数$n$に対して
\begin{align*}\Gamma(n+1)=n!\end{align*}
が成り立つ.
数学的帰納法により示す.
[1]$\Gamma(0+1)=\Gamma(1)=1=0!$だから,$n=0$のときは成り立つ.
[2]ある$n\in\N$に対して$\Gamma(n+1)=n!$が成り立つと仮定すると,$\Gamma(x+1)$と$\Gamma(x)$の関係より
\begin{align*}\Gamma((n+1)+1)=\Gamma(n+2)=(n+1)\Gamma(n+1)=(n+1)\cdot n!=(n+1)!\end{align*}
が成り立つ.
ベータ関数との関係
ガンマ関数と関係の深い関数にベータ関数があります.ベータ関数の定義は次の通りです.
正の実数$x$, $y$に対して
\begin{align*}B(x,y)=\int_{0}^{1}t^{x-1}(1-t)^{y-1}\,dt\end{align*}
で定まる2変数関数$B$をベータ関数(beta function)という.
$t=\sin^2{\theta}$と置換することにより,
\begin{align*}B(x,y)
&=\int_{0}^{1}(\sin^2{\theta})^{x-1}(1-\sin^2{\theta})^{y-1}\cdot2\sin{\theta}\cos{\theta}\,d\theta
\\&=2\int_{0}^{\frac{\pi}{2}}\sin^{2x-1}{\theta}\cos^{2y-1}{\theta}\,d\theta\end{align*}
とも表せますね.
さて,ガンマ関数を用いると,ベータ関数は以下のように表せます.
正の実数$x$, $y$に対して
\begin{align*}B(x,y)=\frac{\Gamma(x)\Gamma(y)}{\Gamma(x+y)}\end{align*}
が成り立つ.
$\Gamma(x)\Gamma(y)=\Gamma(x+y)B(x,y)$を示せばよい.先ほど説明したガンマ関数の別の表し方を用いると
\begin{align*}\Gamma(x)\Gamma(y)
&=\bra{2\int_{0}^{\infty}u^{2x-1}e^{-u^2}\,du}\bra{2\int_{0}^{\infty}v^{2y-1}e^{-v^2}\,dv}
\\&=4\int_{0}^{\infty}\bra{\int_{0}^{\infty}u^{2x-1}v^{2y-1}e^{-u^2-v^2}\,du}\,dv\end{align*}
である.極座標変換$(u,v)=(r\cos{\theta},r\sin{\theta})$を用いると,ヤコビアンが$r$であることに注意して
\begin{align*}\Gamma(x)\Gamma(y)
&=\int_{0}^{\infty}\bra{\int_{0}^{\frac{\pi}{2}}r(r\cos{\theta})^{2x-1}(r\sin{\theta})^{2y-1}e^{-r^2}\,d\theta} dr
\\&=\bra{2\int_{0}^{\infty}r^{2(x+y)-1}e^{-r^2}\,dr}\bra{2\int_{0}^{\frac{\pi}{2}}\cos^{2x-1}{\theta}\sin^{2x-1}{\theta}d\theta}\end{align*}
となる.上で示したガンマ関数の別の表し方から$\Gamma(x+y)=2\dint_{0}^{\infty}r^{2(x+y)-1}e^{-r^2}\,dr$であり,一方$t=\sin^2{\theta}$と置けば
\begin{align*}&2\int_{0}^{\frac{\pi}{2}}\sin^{2x-1}{\theta}\cos^{2y-1}{\theta}\,d\theta
\\&=\int_{0}^{1}(\sin^2{\theta})^{x-1}(1-\sin^2{\theta})^{y-1}(2\sin{\theta}\cos{\theta}\,d\theta)
=B(x,y)\end{align*}
となる.以上より$\Gamma(x)\Gamma(y)=\Gamma(x+y)B(x,y)$を得る.
補足
最後にいくつか補足します.
複素関数としてのガンマ関数
ガンマ関数は複素変数に対しても定義されます.
実部が正の複素数$z$に対して
\begin{align*}\Gamma(z)=\int_{0}^{\infty}t^{z-1}e^{-t}\,dt\end{align*}
で定まる複素関数$\Gamma$をガンマ関数(gamma function)という.
ただし,$t^{z}$は$t^{z}=e^{z\log{t}}$で定まる複素数である.
実数の場合と同様に次が成り立ちます.
実部が正の実数$z$に対して
\begin{align*}\Gamma(z+1)=z\Gamma(z)\end{align*}
が成り立つ.
複素関数論においてガンマ関数は非常に興味深い正則関数ですが,この記事では以上の説明に留めます.
広義積分としてのガンマ関数
ガンマ関数$\Gamma(z)=\int_{0}^{\infty}t^{x-1}e^{-t}\,dt$の被積分関数$t^{x-1}e^{-t}$は,$x<1$のときは$t$が負冪になるので$t=0$では定義されません.そのため,$x<1$のときは
- 0付近での積分
- 無限遠方までの積分
のふたつの意味で広義積分となっており,このことをきちんと表すと
\begin{align*}\Gamma(z):=\lim_{\substack{r\to+0\\R\to\infty}}\int_{r}^{R}t^{x-1}e^{-t}\,dt\end{align*}
ということになりますね.
一方,$x\ge1$のときは$t=0$でも定義されるので,無限遠方までの積分の意味で広義積分となっており,
\begin{align*}\Gamma(z):=\lim_{R\to\infty}\int_{0}^{R}t^{x-1}e^{-t}\,dt\end{align*}
ということになりますね.
ガンマ関数が収束することの証明
そもそも「ガンマ関数$\Gamma$を正の実数$x$に対して
\begin{align*}\Gamma(x)=\int_{0}^{\infty}t^{x-1}e^{-t}\,dt\end{align*}
と定める」というためには,正の実数$x$に対して広義積分$\int_{0}^{\infty}t^{x-1}e^{-t}\,dt$が収束していることを示さないといけませんね.
直観的には,$t$について
- 無限遠方では($t^{x-1}$よりも)指数減衰$e^{-t}$が強いので収束
- 0付近では$e^{-t}\approx1$なので$t^{x-1}$の増大(特異性)が弱ければ収束
ということになりますね.
正の実数$x$に対して,広義積分$\dint_{0}^{\infty}t^{x-1}e^{-t}\,dt$は収束する.すなわち,$\Gamma(x)$は有限の値をとる.
極限$\lim\limits_{t\to\infty}t^{x-1}e^{-\frac{t}{2}}=0$より,ある$T>0$が存在して,$t\ge T$で
\begin{align*}t^{x-1}e^{-\frac{t}{2}}\le1
\iff t^{x-1}e^{-t}\le e^{-\frac{t}{2}}\end{align*}
が成り立つ.以下,$\int_{T}^{\infty}t^{x-1}e^{-t}\,dt$, $\int_{0}^{T}t^{x-1}e^{-t}\,dt$の両方が収束することを示す.
これらが示されれば,広義積分$\int_{0}^{\infty}t^{x-1}e^{-t}\,dt$が収束することが分かる.
$[T,\infty)$での積分
被積分関数$t^{x-1}e^{-t}$は$t\ge T$で非負値で,
\begin{align*}\int_{T}^{\infty}t^{x-1}e^{-t}\,dt
\le\int_{T}^{\infty}e^{-\frac{t}{2}}\,dt
=\brc{-2e^{-\frac{t}{2}}}_{T}^{\infty}
=2e^{-\frac{T}{2}}<\infty\end{align*}
なので,$\int_{T}^{\infty}t^{x-1}e^{-t}\,dt$は収束する.
$[0,T]$での積分($(0,T]$での広義積分)
$0\le t\le T$で$e^{-t}\le1$だから,
\begin{align*}&\int_{0}^{T}t^{x-1}e^{-t}\,dt
\le\int_{0}^{T}t^{x-1}\,dt
=\brc{\frac{1}{x}t^{x}}_{0}^{T}
=\frac{1}{x}T^{x}<\infty\end{align*}
なので,$\int_{T}^{\infty}t^{x-1}e^{-t}\,dt$は収束する.ただし,
- 一つ目の等号では$x-1\neq-1$であること
- 二つ目の等号では$x>0$であること
に注意.
一方,$x\le0$のときは0付近で$t^{x-1}$の増大が大きく,$\int_{0}^{1}t^{x-1}e^{-t}\,dt$が発散します.実際,$x=0$なら
\begin{align*}&\int_{0}^{1}t^{0-1}e^{-t}\,dt\ge\int_{0}^{1}t^{-1}e^{-1}\,dt=\frac{1}{e}[\log{t}]_{0}^{1}=\infty\end{align*}
と発散し,$x<0$なら$\lim\limits_{t\to+0}t^{x}=\infty$なので
\begin{align*}&\int_{0}^{T}t^{x-1}e^{-t}\,dt\le\int_{0}^{T}t^{x-1}\,dt=\brc{\frac{1}{x}t^{x}}_{0}^{T}=\infty\end{align*}
と発散しますね.

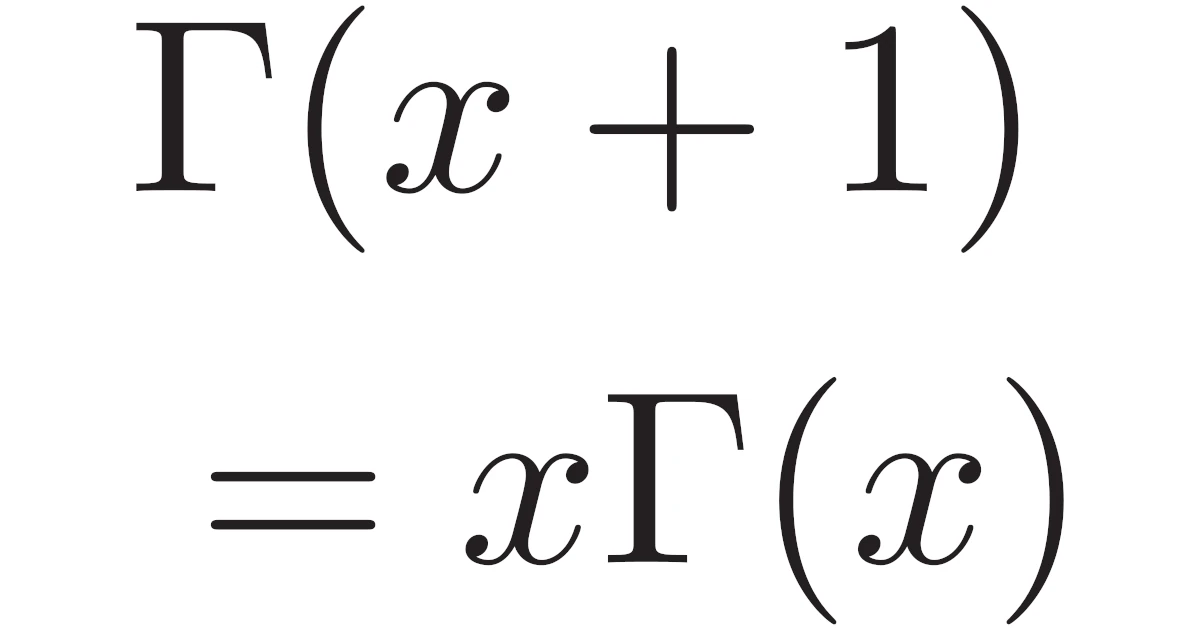
コメント