微分積分学では三角関数$\cos{x}$, $\sin{x}$と指数関数$e^x$はそれぞれ
\begin{align*}&\cos{x}=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\dots,
\\&\sin{x}=\frac{x}{1!}-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\dots,
\\&e^z=1+\frac{z}{1!}+\frac{z^2}{2!}+\frac{z^3}{3!}+\frac{z^4}{4!}+\dots\end{align*}
とテイラー展開できることを学びます.
このことをふまえて,複素関数の三角関数$\cos{z}$, $\sin{z}$と指数関数$e^z$は整級数(冪級数)を用いて定義するのが一般的です.
この記事では
- 三角関数$\cos{z}$, $\sin{z}$と指数関数$e^z$の定義と基本性質
- オイラーの公式と諸性質
- 指数法則と三角関数の加法定理
を順に解説します.
三角関数$\cos{z}$, $\sin{z}$と指数関数$e^z$の定義と基本性質
まずは三角関数$\cos{z}$, $\sin{z}$と指数関数$e^z$を複素関数として定義しましょう.
収束半径∞の3つの整級数
実関数$\cos{x}$, $\sin{x}$, $e^x$のテイラー展開で$x$を複素変数$z$に置き換えた整級数の収束半径はいずれも∞です.
$\C$上の整級数
\begin{align*}&1-\frac{z^2}{2!}+\frac{z^4}{4!}-\frac{z^6}{6!}+\dots\bra{=\sum_{n=0}^{\infty}\frac{(-1)^n z^{2n}}{(2n)!}},
\\&\frac{z}{1!}-\frac{z^3}{3!}+\frac{z^5}{5!}-\frac{z^7}{7!}+\dots\bra{=\sum_{n=0}^{\infty}\frac{(-1)^n z^{2n+1}}{(2n+1)!}},
\\&1+\frac{z}{1!}+\frac{z^2}{2!}+\frac{z^3}{3!}+\frac{z^4}{4!}+\dots\bra{=\sum_{n=0}^{\infty}\frac{z^n}{n!}}\end{align*}
の収束半径はいずれも∞である.
任意の$R>0$に対して
\begin{align*}&\abs{\left.\frac{(-1)^{n+1}R^{2(n+1)}}{(2(n+1))!}\middle/\frac{(-1)^nR^{2n}}{(2n)!}\right.}
\\&=\frac{R^2}{(2n+2)(2n+1)}\xrightarrow[]{n\to\infty}0<1\end{align*}
だから,ダランベールの判定法(ratio test)より,正項級数$\sum\limits_{n=0}^{\infty}\abs{\frac{(-1)^n R^{2n}}{(2n)!}}$は収束する.
よって,整級数$\sum\limits_{n=0}^{\infty}\frac{(-1)^n z^{2n}}{(2n)!}$は$\set{z\in\C}{|z|<R}$で収束する.$R$の任意性より,級数$\sum\limits_{n=0}^{\infty}\frac{(-1)^n z^{2n}}{(2n)!}$の収束半径は$\infty$である.
また,
\begin{align*}&\abs{\left.\frac{(-1)^{n+1} R^{2(n+1)+1}}{(2(n+1)+1)!}\middle/\frac{(-1)^n R^{2n+1}}{(2n+1)!}\right.}
\\&=\frac{R^2}{(2n+3)(2n+2)}\xrightarrow[]{n\to\infty}0<1,
\\&\abs{\left.\frac{R^{n+1}}{(n+1)!}\middle/\frac{R^n}{n!}\right.}=\frac{R}{n+1}\xrightarrow[]{n\to\infty}0<1\end{align*}
だから,同様に級数$\sum\limits_{n=0}^{\infty}\frac{(-1)^n z^{2n+1}}{(2n+1)!}$, $\sum\limits_{n=0}^{\infty}\frac{z^n}{n!}$の収束半径も$\infty$である.
三角関数$\cos{z}$, $\sin{z}$と指数関数$e^z$を整級数で定める
補題の3つの級数をそれぞれ$\cos{z}$, $\sin{z}$, $e^z$と定めます.
三角関数$\cos{z}$, $\sin{z}$と指数関数$e^z$を
\begin{align*}&\cos{z}=1-\frac{z^2}{2!}+\frac{z^4}{4!}-\frac{z^6}{6!}+\dots,
\\&\sin{z}=\frac{z}{1!}-\frac{z^3}{3!}+\frac{z^5}{5!}-\frac{z^7}{7!}+\dots,\quad
\\&e^z=1+\frac{z}{1!}+\frac{z^2}{2!}+\frac{z^3}{3!}+\frac{z^4}{4!}+\dots\end{align*}
で定める.$e^{z}$は$\exp{(z)}$と表すこともある.
$z$が実変数$x$のときは,実関数の三角関数$\cos{x}$, $\sin{x}$と指数関数$e^x$のテイラー展開に一致しますから,実関数の場合に矛盾しない定義になっています.
三角関数$\cos{z}$, $\sin{z}$と指数関数$e^z$の導関数
一般に整級数は収束円板内で正則で項別微分可能でしたから,これら3つの整級数は収束半径が∞であることと併せて,いずれも整関数($\C$全体での正則関数)になっており,導関数が実関数の場合と同様に次のようになることも分かります.
三角関数$\cos{z}$, $\sin{z}$と指数関数$e^z$は整級数で,それぞれの導関数は
\begin{align*}&(\cos{z})’=-\sin{z},\quad
(\sin{z})’=\cos{z},\quad
(e^z)’=e^z\end{align*}
である.
補題より三角関数$\cos{z}$, $\sin{z}$と指数関数$e^z$の定義の整級数は$\C$上で項別微分可能なので,
\begin{align*}(\cos{z})’&=\bra{1-\frac{z^2}{2!}+\frac{z^4}{4!}-\frac{z^6}{6!}+\dots}’
\\&=-\bra{\frac{z}{1!}-\frac{z^3}{3!}+\frac{z^5}{5!}-\dots}=-\sin{z},
\\(\sin{z})’&=\bra{\frac{z}{1!}-\frac{z^3}{3!}+\frac{z^5}{5!}-\frac{z^7}{7!}+\dots}’
\\&=1-\frac{z^2}{2!}+\frac{z^4}{4!}-\frac{z^6}{6!}+\dots=\cos{z},
\\(e^z)’&=\bra{1+\frac{z}{1!}+\frac{z^2}{2!}+\frac{z^3}{3!}+\frac{z^4}{4!}+\dots}’
\\&=1+\frac{z}{1!}+\frac{z^2}{2!}+\frac{z^3}{3!}+\dots=e^z\end{align*}
が成り立つ.
$\cos{(-z)}$, $\sin{(-z)}$を$\cos{z}$, $\sin{z}$で表す
三角関数について$\cos{(-z)}$, $\sin{(-z)}$は,実関数の場合と同様に次のようになります.
任意の$z\in\C$に対して,
\begin{align*}&\cos{(-z)}=\cos{z},\quad
\sin{(-z)}=-\sin{z}\end{align*}
が成り立つ.
指数関数$\cos{z}$, $\sin{z}$の定義より
\begin{align*}\cos{(-z)}&=1-\frac{(-z)^2}{2!}+\frac{(-z)^4}{4!}-\frac{(-z)^6}{6!}+\dots
\\&=1-\frac{z^2}{2!}+\frac{z^4}{4!}-\frac{z^6}{6!}+\dots=\cos{z},
\\\sin{(-z)}&=\frac{-z}{1!}-\frac{(-z)^3}{3!}+\frac{(-z)^5}{5!}-\frac{(-z)^7}{7!}+\dots
\\&=\bra{\frac{z}{1!}-\frac{z^3}{3!}+\frac{z^5}{5!}-\frac{z^7}{7!}+\dots}=-\sin{z}\end{align*}
が成り立つ.
オイラーの公式と諸性質
整級数による三角関数$\cos{z}$, $\sin{z}$と指数関数$e^z$の定義から,これらの重要な関係式であるオイラーの公式が証明できます.
オイラーの公式は整級数の定義から得られる
[オイラーの公式]任意の$z\in\C$に対して$e^{iz}=\cos{z}+i\sin{z}$が成り立つ.
任意の$z\in\C$に対して,$\cos{z}$, $\sin{z}$の定義の整級数は絶対収束するから,級数の和の順序を変えても等しく
\begin{align*}&\cos{z}+i\sin{z}
\\&=\bra{1-\frac{z^2}{2!}+\frac{z^4}{4!}-\frac{z^6}{6!}+\dots}
+i\bra{\frac{z}{1!}-\frac{z^3}{3!}+\frac{z^5}{5!}-\frac{z^7}{7!}+\dots}
\\&=1+\frac{iz}{1!}-\frac{z^2}{2!}-\frac{iz^3}{3!}+\frac{z^4}{4!}+\frac{iz^5}{5!}-\frac{z^6}{6!}-\frac{iz^7}{7!}+\dots
\\&=1+\frac{iz}{1!}+\frac{(iz)^2}{2!}+\frac{(iz)^3}{3!}+\frac{(iz)^4}{4!}+\frac{(iz)^5}{5!}+\frac{(iz)^6}{6!}+\frac{(iz)^7}{7!}+\dots
\\&=\sum_{n=0}^{\infty}\frac{(iz)^n}{n!}=e^{iz}\end{align*}
が成り立つ.
三角関数$\cos{z}$, $\sin{z}$を指数関数$e^z$で表す
オイラーの公式と$\cos{(-z)}=\cos{z}$, $\sin{(-z)}=-\sin{z}$から,$\cos{z}$, $\sin{z}$は$e^{z}$を用いて表せることが分かります.
任意の$z\in\C$に対して$\cos{z}=\frac{e^{iz}+e^{-iz}}{2}$, $\sin{z}=\frac{e^{iz}-e^{-iz}}{2i}$が成り立つ.
任意の$z\in\C$に対して,
\begin{align*}&e^{-iz}=\cos{(-z)}+i\sin{(-z)}=\cos{z}-i\sin{z}\end{align*}
だから,
\begin{align*}&e^{iz}+e^{-iz}=2\cos{z},\quad
e^{iz}-e^{-iz}=2i\sin{z}\end{align*}
なので,$\cos{z}=\frac{e^{iz}+e^{-iz}}{2}$, $\sin{z}=\frac{e^{iz}-e^{-iz}}{2i}$が成り立つ.
$e^{z}$だけを整級数で定義しておいて,$\cos{z}$, $\sin{z}$をこの命題の等式で定義することもありますが,いずれにしても全く同じものになります.
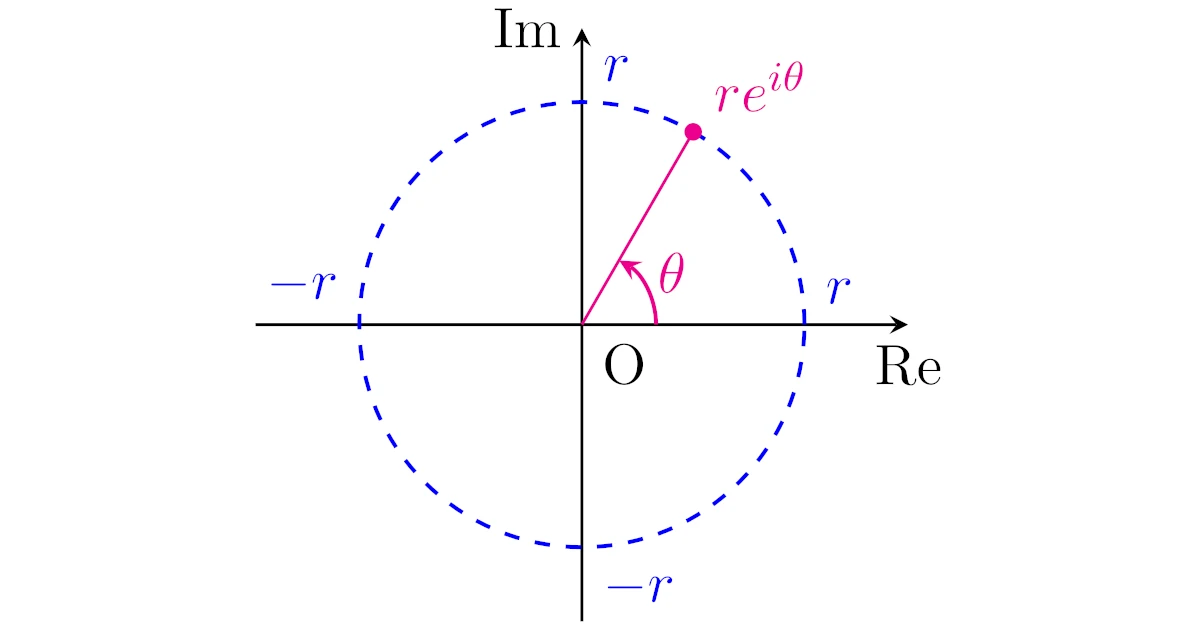
実数$\theta$に対して$re^{i\theta}$は極形式を表す
オイラーの公式$e^{iz}=\cos{z}+i\sin{z}$は$z\in\C$に対して成り立ちますが,$z$が実数の場合にもよく用いられます.とくに極形式を$re^{i\theta}$で表せることは重要です.
絶対値$r\ge0$,偏角$\theta\in\R$の複素数は$re^{i\theta}$と表せる:$re^{i\theta}=r(\cos{\theta}+i\sin{\theta})$.
絶対値$r\ge0$,偏角$\theta\in\R$の複素数は,極形式で$r(\cos{\theta}+i\sin{\theta})$と表せる.
また,オイラーの公式より$e^{i\theta}=\cos{\theta}+i\sin{\theta}$だから$r(\cos{\theta}+i\sin{\theta})=re^{i\theta}$である.
とくに絶対値1の複素数は$\theta\in\R$を用いて$e^{i\theta}$と表せることはよく用います.さらに$\theta=\pi$とすると$e^{\pi i}=-1$となり,この等式をオイラーの等式といいます.
指数法則と三角関数の加法定理
$a^n$を「$a$を$n$回かけたもの」として定義すれば,指数法則$a^{n+m}=a^{n}a^{m}$($m,n\in\N$)はほとんど当たり前です.
複素関数として整関数で定義した指数関数$e^z$でも指数法則$e^{z+w}=e^{z}e^{w}$は成り立ちますが,証明には少し計算をする必要があります.
指数法則は整級数の積を展開して得られる
まずは一般に成り立つ整級数の積に関する次の補題を確認しておきましょう.
級数$\sum\limits_{n=0}^{\infty}a_n$, $\sum\limits_{n=0}^{\infty}b_n$が絶対収束するとき,
\begin{align*}a_0b_0+(a_1b_0+a_0b_1)+(a_2b_0+a_1b_1+a_0b_2)+\dots\bra{=\sum_{n=0}^{\infty}\sum_{k=0}^{n}a_{k}b_{n-k}}\end{align*}
は絶対収束して,積$\bra{\sum\limits_{n=0}^{\infty}a_n}{\sum\limits_{n=0}^{\infty}b_n}$に等しい.
2つの級数の積\bra{\sum\limits_{n=0}^{\infty}a_n}\bra{\sum\limits_{n=0}^{\infty}b_n}$を形式的に展開すると$\sum_{n=0}^{\infty}\sum_{k=0}^{n}a_{k}b_{n-k}$となるので,もとの2つの級数が絶対収束していれば,これらが等しいことがきちんと証明できるというわけですね.
この補題をもとに,指数法則$e^{z+w}=e^{z}e^{w}$を示しましょう.
[指数法則]任意の$z,w\in\C$に対して,$e^{z+w}=e^{z}e^{w}$が成り立つ.
任意の$z,w\in\C$に対して,$e^{z}$, $e^{w}$の定義の整級数はともに絶対収束するから
\begin{align*}e^{z}e^{w}&=\bra{\sum_{n=0}^{\infty}\frac{z^n}{n!}}\bra{\sum_{n=0}^{\infty}\frac{w^n}{n!}}
\\&=\sum_{n=0}^{\infty}\sum_{k=0}^{n}\frac{z^k}{k!}\frac{w^{n-k}}{(n-k)!}
\\&=\sum_{n=0}^{\infty}\frac{1}{n!}\sum_{k=0}^{n}\frac{n!}{k!(n-k)!}z^kw^{n-k}
\\&=\sum_{n=0}^{\infty}\frac{(z+w)^{n}}{n!}=e^{z+w}\end{align*}
が成り立つ.ただし,最後から2つ目の等号では二項定理を用いた.
指数関数$e^{z}$は0以外の複素数を表す周期関数
指数関数$e^{z}$は値域$\C\setminus\{0\}$で周期$2\pi i$の周期関数である.
一般に任意の$z\in\C$に対して$f(z+\alpha)=f(z)$を満たす複素関数$f$を周期$\alpha$の周期関数といいます.
任意の$z\in\C$に対して,$z=x+iy\in\C$($x,y\in\R$)とおく.指数法則とオイラーの公式より
\begin{align*}e^{z}=e^{x+yi}=e^{x}e^{iy}\end{align*}
だから,$e^{z}$は絶対値$e^{x}$,偏角$y$の複素数を表す.$e^{x}>0$なので$e^{z}$の値域は$\C\setminus\{0\}$である.また,
\begin{align*}e^{2\pi i}=\cos{(2\pi i)}+i\sin{(2\pi i)}=1\end{align*}
だから,$e^{z+2\pi i}=e^{z}e^{2\pi i}=e^{z}$なので$e^{z}$は周期$2\pi i$の周期関数である.
指数法則とオイラーの公式から三角関数の加法定理が得られる
実関数の三角関数で加法定理が成り立ったように,複素関数の三角関数でも同様に加法定理が成り立ちます.
[加法定理]任意の$z,w\in\C$に対して,
\begin{align*}&\cos{(z+w)}=\cos{z}\cos{w}-\sin{z}\sin{w},
\\&\sin{(z+w)}=\sin{z}\cos{w}+\cos{z}\sin{w}\end{align*}
が成り立つ.
任意の$z,w\in\C$に対して,指数法則とオイラーの公式より
\begin{align*}2\cos{(z+w)}&=e^{i(z+w)}+e^{-i(z+w)}=e^{iz}e^{iw}+e^{-iz}e^{-iw}
\\&=(\cos{z}+i\sin{z})(\cos{w}+i\sin{w})+(\cos{(-z)}+i\sin{(-z)})(\cos{(-w)}+i\sin{(-w)})
\\&=(\cos{z}+i\sin{z})(\cos{w}+i\sin{w})+(\cos{z}-i\sin{z})(\cos{w}-i\sin{w})
\\&=\{(\cos{z}\cos{w}-\sin{z}\sin{w})+i(\cos{z}\sin{w}+\sin{z}\cos{w})\}
\\&+\{(\cos{z}\cos{w}-\sin{z}\sin{w})-i(\cos{z}\sin{w}+\sin{z}\cos{w})\}
\\&=2(\cos{z}\cos{w}-\sin{z}\sin{w})\end{align*}
だから,$\cos{(z+w)}=\cos{z}\cos{w}-\sin{z}\sin{w}$を得る.同様に
\begin{align*}2i\sin{(z+w)}&=e^{i(z+w)-e^{-i(z+w)}
\\&=\{(\cos{z}\cos{w}-\sin{z}\sin{w})+i(\cos{z}\sin{w}+\sin{z}\cos{w})\}
\\&-\{(\cos{z}\cos{w}-\sin{z}\sin{w})-i(\cos{z}\sin{w}+\sin{z}\cos{w})\}
\\&=2i(\cos{z}\sin{w}+\sin{z}\cos{w})\end{align*}
だから,$\sin{(z+w)}=\sin{z}\cos{w}+\cos{z}\sin{w}$を得る.


コメント