テストの点数などの数値データがあるとき,データの中心を表す量として平均値がよく使われます.
しかし,平均値は外れ値の影響を受けやすく,平均値がデータの中心としてあまり適切でないこともあります.
例えば,日本成人の年収を考えたとき,一部高所得者がいることで平均年収が高く吊り上げられてしまい,年収の中央値と平均値に小さくない差が出ます.
さて,外れ値がたくさんあるデータは「データがばらついている」ということができますが,データのばらつきを表す指標として分散と標準偏差があります.
この記事では,
- データの分散のイメージ
- データの分散の定義
- データの標準偏差の定義とイメージ
を説明します.
「統計データの記述」の一連の記事
データの「ばらつき」と分散
以下のような7人の生徒の2つのテストの成績(データ)を考えます.
| 生徒 | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| テスト1の点数 | 80 | 72 | 83 | 92 | 67 | 77 | 75 |
| テスト2の点数 | 65 | 58 | 60 | 69 | 62 | 56 | 71 |
このテスト1の点数の平均値は
\begin{align*}\frac{80+72+83+92+67+77+75}{7}=78\end{align*}
で,テスト2の点数の平均値は
\begin{align*}\frac{65+58+60+69+62+56+71}{7}=63\end{align*}
ですね.
データの「ばらつき」の考え方
さて,テスト1の点数とテスト2の点数でどちらの方がばらついていると言えるでしょうか?
テスト1の点数とそれらの平均値を数直線上に表すと下図のようになります.
同様に,テスト2の点数とそれらの平均値を数直線上に表すと下図のようになります.
ぱっと見でテスト1の方が点数がばらついているように見えますが,このばらつき度合いを数値で表すにはどうすればいいでしょうか?
データの平均からの離れ具合
データのばらつきを考えるには,データの各数値が平均値からどれくらい離れているかを考えます.
例えば,テスト1において
- 平均値の78点からB君の72点を引くと$78-72=6$
- 平均値の78点からD君の92点を引くと$78-92=-14$
です.
このように全てのデータを平均から引いて,さらにこの平均との差を2乗すると,それぞれデータは
- 80 → $(78-80)^2=(-2)^2=4$
- 72 → $(78-72)^2=6^2=36$
- 83 → $(78-83)^2=(-5)^2=25$
- 92 → $(78-92)^2=(-14)^2=196$
- 67 → $(78-67)^2=11^2=121$
- 77 → $(78-77)^2=1^2=1$
- 75 → $(78-75)^2=3^2=9$
となりますね.この2乗した後の値が大きいほど平均値から遠いので,この値の平均値をとるとデータ全体の平均値からのばらつき度合いが分かりますね.
つまり,テスト1の点数の平均値からのばらつき度合いは
\begin{align*}\frac{4+36+25+196+121+1+9}{7}=56\end{align*}
と考えることができます.同様に,テスト2の点数の平均値からのばらつき度合いは
\begin{align*}&\frac{(63-65)^2+(63-58)^2+(63-60)^2+(63-69)^2+(63-62)^2+(63-56)^2+(63-71)^2}{7}
\\&=\frac{(-2)^2+5^2+3^2+(-6)^2+1^2+7^2+(-8)^2}{7}
\\&=\frac{4+25+9+36+1+49+64}{7}
=\frac{149}{7}\end{align*}
と考えることができます.このようにして得られた値を分散といいます.
データの分散の定義
一般に数値データの分散は次のように定義されます.
データ$x_1,\dots,x_n$の平均値を$\overline{x}$とするとき,
\begin{align*}\sigma^2=\frac{(\overline{x}-x_1)^2+(\overline{x}-x_2)^2+\dots+(\overline{x}-x_n)^2}{n}\end{align*}
をこのデータの分散(variance)という.
和の記号$\sum$を用いると$\sigma^2=\frac{1}{n}\sum\limits_{k=1}^{n}(\overline{x}-x_k)^2$とも表せますね.
分散とは「各データ$x_k$を平均$\overline{x}$から引いた差$\overline{x}-x_k$を2乗したものの平均値」ということもできますね.
上で計算したように
- テスト1の点数の分散は$56$
- テスト2の点数の分散は$\dfrac{149}{7}=21.\dots$
なので,確かにテスト1の方が分散が大きく,平均値からばらついていると言えますね.
平均値が実態を表さない例
この記事の冒頭で「平均値は外れ値の影響を受けやすく,平均値がデータの中心としてあまり適切でないこともあります」と書きました.
例えば,テスト3の結果が以下のように極端なものになったとしましょう.
| 生徒 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| テスト3の点数 | 0 | 0 | 100 | 100 | 0 | 100 |
このとき,平均値は
\begin{align*}\frac{0+0+100+100+0+100}{6}=50\end{align*}
となります.しかし,この50は適切にデータの実態を表しているようには思えませんね.
そこで,このテスト3の点数の分散$\sigma^2$を求めると
\begin{align*}\sigma^2&=\frac{(50-0)^2+(50-0)^2+(50-100)^2+(50-100)^2+(50-0)^2+(50-100)^2}{6}
\\&=\frac{50^2+50^2+50^2+50^2+50^2+50^2}{6}=2500\end{align*}
と計算されますが,この2500という値はテスト1の点数の分散$56$やテスト2の点数の分散$\dfrac{149}{7}$と比べるとかなり大きいです.
このことから「テスト3の点数はばらつきが大きいため,平均点が実態を表していない可能性が高い」と判断できます.
標準偏差
分散と同じくデータのばらつきを表す重要な指標として標準偏差があります.
分散で2乗している理由
分散を求めるときに平均値からデータを引いた値を「2乗」しているのはなぜでしょうか?
もし,テスト3の点数で平均との差を2乗せず足し合わせたとすると
\begin{align*}&\frac{(50-0)+(50-0)+(50-100)+(50-100)+(50-0)+(50-100)}{6}
\\&=\frac{50+50-50-50+50-50}{6}=0\end{align*}
となってしまい,平均値からの「右へのばらつき」と「左へのばらつき」が打ち消しあって0となってしまいました(どのようなデータでも,この計算をすると必ず0になることが証明できます).
一方,2乗すると必ず0以上の値になることから,2乗すればこのような相殺が起こらず平均値からのばらつきを足し合わせられるというわけですね.
相殺が起こらないようにするために絶対値を考える指標(平均絶対偏差)もありますが,通常の2乗する分散の方が使い勝手が良いことも多いので,まずは分散を理解しておきましょう.
標準偏差のイメージと定義
分散$\sigma^2$は平均値との差の2乗の和の平均を考えていることから,「分散$\sigma^2$の正の平方根」は平均値とデータの差のだいたい1乗分の平均を考えていることになります.
そこで「分散の正の平方根」を標準偏差といいます.
データ$x_1,\dots,x_n$の平均値を$\overline{x}$とするとき,
\begin{align*}\sigma=\sqrt{\frac{(\overline{x}-x_1)^2+(\overline{x}-x_2)^2+\dots+(\overline{x}-x_n)^2}{n}}\end{align*}
をこのデータの標準偏差(standard deviation)という.
和の記号$\sum$を用いると$\sigma=\sqrt{\frac{1}{n}\sum\limits_{k=1}^{n}(\overline{x}-x_k)^2}$とも表せますね.
例えば,テスト3の点数の分散は$2500$でしたから,標準偏差は
\begin{align*}\sqrt{2500}=50\end{align*}
となり,確かに全てのデータが平均値から50点離れていることを表せていますね.
同様に,テスト1の点数の分散は$56$で,テスト2の点数の分散は$\dfrac{149}{7}$でしたから,それぞれのテストの標準偏差は
\begin{align*}\sqrt{56}=7.48\dots,\quad
\sqrt{\dfrac{149}{7}}=4.61\dots\end{align*}
となって,テスト1の平均値からの離れ具合は7.48点程度,テスト2の平均値からの離れ具合は4.61点程度と考えることができますね.
参考文献
以下は参考文献です.
改訂版 統計検定2級対応 統計学基礎
[日本統計学会 編/東京図書]
統計検定2級は「大学基礎科目(学部1,2年程度)としての統計学の知識と問題解決能力」という位置付けであり,ある程度の数学的な処理能力が求められます.
そのため,統計検定2級を取得していると,一定以上の統計的なデータの扱い方を身に付けているという指標になります.
日本統計学会が実施する「統計検定」の2級の範囲に対応する教科書なので,「2級の試験範囲を確認する」くらいのつもりで持っておくのが良いかもしれません.
しかし,このテキストは表面的な説明に留まっているなど読みづらい部分も多いので,本書だけで2級の対策をするのは少し難しいと思います.
大学1年の微分積分学の知識は必要なので,もし自信がなければ統計検定3級からの挑戦を検討しても良いでしょう.
なお,本書については,以下の記事で書評としてまとめています.
【教科書紹介|統計検定2級対応 統計学基礎(日本統計学会編)】
本書の目次・必要な知識・良い点と気になる点・オススメの使い方などをレビューしています.

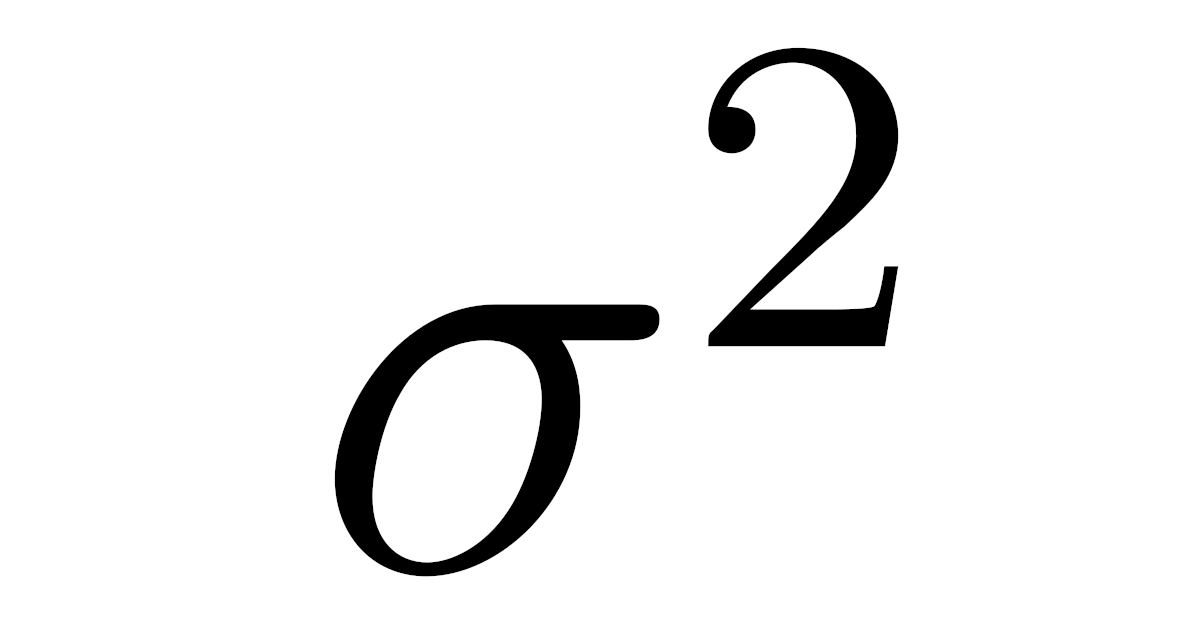

コメント