教科書紹介｜統計検定２級対応 統計学基礎（日本統計学会編）

東京図書から発刊されている「統計検定２級対応 統計学基礎」（日本統計学会編，東京図書）は日本統計学会の統計検定２級公式の教科書です．

統計検定は日本統計学会が実施する検定で１級・準１級・２級・３級・４級があります．

統計検定２級は「大学基礎科目としての統計学の知識と問題解決能力」を測るものとしており，大学１年生程度のレベルが要求されます．

本書は統計検定２級で出題される範囲に即した内容のテキストとなっており，出題範囲を把握するためにもっておくと良いでしょう．

また，広くトピックが扱われているので，統計の基礎的な分野の概観を見渡すのに良いテキストということができます．

統計検定２級について詳しくは，以下を参照してください．

統計検定２級｜統計検定：Japan Statistical Society Certificate

「統計検定」とは、統計に関する知識や活用力を評価する全国統一試験です。問い合わせ：統計検定センター

www.toukei-kentei.jp

目次

以下は本書の目次です．

第１章：データの記述と要約

1. 変数の分類
2. 量的データの分布
   1. ヒストグラムの作成
   2. そのほかの図表の作成
3. 分布の特徴を表す指標
   1. 平均・分散・標準偏差
   2. 標準化得点
   3. 変動係数
   4. 中央値・最頻値
   5. 範囲・四分位範囲
4. 量的データの要約とグラフ表現
   1. ５数要約
   2. 箱ひげ図
   3. 外れ値
5. 質的データの度数分布とグラフ表現
6. ２変数データの記述と要約
   1. 散布図
   2. 相関係数
   3. 偏相関係数
   4. 回帰直線
   5. 質的データのクロス集計表
7. 時系列データの記述と簡単な分析
   1. 時系列データ
   2. 指数化と幾何平均
   3. 時系列データの変動分解
   4. 自己相関
   5. 指数の作成と利用

第２章：確率と確率分布

1. 事象と確率
2. 条件付き確率
3. ベイズの定理
4. 確率変数と確率分布
5. 期待値と分散
6. モーメント
7. 主な離散型確率分布
   1. ベルヌーイ分布
   2. 二項分布
   3. ポアソン分布
   4. 幾何分布
8. 主な連続型確率分布
   1. 一様分布
   2. 正規分布
   3. 指数分布
9. ２変数の確率分布
   1. 同時分布と周辺分布
   2. 共分散と相関係数
   3. ２変量正規分布
10. 標本分布
    1. $\chi^2$分布
    2. $t$分布
    3. $F$分布
11. 大数の法則と中心極限定理
    1. チェビシェフの不等式
    2. 大数の法則
    3. 中心極限定理

第３章：統計的推定

1. 母集団と標本
   1. 母集団と標本
   2. 調査と母集団との対応付け
2. 統計的な研究の種類
   1. 実験研究のデザイン
   2. 観察研究のデザイン
   3. 標本調査と抽出方法
3. 点推定と区間推定
   1. 点推定
   2. 区間推定
4. １標本問題：１つの母集団の母数に関する推定−
   1. 正規分布の母平均の推定
   2. 母分散が未知の場合の母平均の推定：$t$分布の利用
   3. 母分散の区間推定
   4. 母比率の推定
5. ２標本問題：２つの母集団の母数に関する推定−
   1. ２つの母平均の差の区間推定
   2. 対応のある２標本の場合
   3. 母分散の比の区間推定
   4. 母比率の差の区間推定

第４章：統計的仮説検定

1. 仮説検定の考え方
2. 基本的な仮説検定の構造
   1. 帰無仮説・対立仮説と有意水準
   2. 片側対立仮説と両側対立仮説
   3. 検定統計量と棄却域
   4. 棄却と受容，２種類の誤り
   5. 母集団の平均に関する仮説
3. １標本問題：１つの母集団の母数に関する検定−
   1. 正規分布の母平均に関する検定(母分散が既知の場合，$z$検定)
   2. 正規分布の母平均に関する検定(母分散が未知の場合，$t$検定)
   3. 母分散に関する検定
   4. 母比率に関する検定
4. ２標本問題：２つの母集団の母数に関する検定−
   1. 母平均の差の検定
   2. 対応のある２標本の場合
   3. 母分散の比の検定
   4. 母比率の差の検定

第５章：線形モデル分析

1. 線形回帰モデル
   1. 線形単回帰モデル
   2. 回帰係数の区間推定
   3. 回帰係数に関する検定
   4. 回帰の現象(平均への回帰)
   5. 線形重回帰モデル
   6. 自由度調整済み決定係数
   7. 回帰の優位性の検定と回帰係数に関する検定
   8. 相関係数の区間推定と検定
2. 分散分析モデル
   1. １元配置分散分析
   2. ２元配置分散分析

第６章：その他の分析法−正規性の検討，適合度と独立性の$\chi^2$検定

1. 正規性の検討
   1. 正規$Q-Q$プロット
   2. 歪度および尖度
2. 適合度の検定
3. 独立性の検定

第７章：付録

1. 確率分布
   1. 超幾何分布
   2. 多項分布
   3. 負の二項分布
   4. 確率分布の間の近似的な関係
2. 仮説検定の基礎的理論
   1. 検出力と検出力関数
   2. ネイマン・ピアソンの基本定理
3. 分散分析の数理
   1. コクランの定理
   2. コクランの定理の応用
4. 多重比較
   1. 検定の多重性
   2. ボンフェローニの不等式
   3. １元配置における各水準の母平均間の多重比較：ボンフェローニ法の応用
5. 確率分布表の引き方
   1. 標準正規分布表
   2. $t$分布表
   3. カイ二乗分布表
   4. $F$分布表
6. Rの使い方
   1. Rのインストール
   2. Rの基本操作
   3. ベクトルと行列
   4. データの読み込み
   5. Rのコマンド例
   6. Rエディタ

• 付表１　標準正規分布の上側確率
• 付表２　$t$分布のパーセント点
• 付表３　カイ二乗分布のパーセント点
• 付表４　$F$分布のパーセント点

必要な知識

本書を読むために必要な知識を挙げます．

高校数学

高校数学で扱う程度の基本的な計算はできないと，とくに後半では読み進めることが難しくなります．

統計では多くのデータを扱うため，データの和などの扱いは数列の分野がベースになります．

姉妹ブログで数列を基礎から解説しているので，数列に不安がある方は是非参照してみてください．

数列１最初の一歩は等差数列と等比数列！

高校数学での数列で基礎となるのは「等差数列」と「等比数列」で，少し複雑な数列も等差数列または等比数列に帰着させることが多いです．この記事では，数列の基礎と等差数列・等比数列を説明します．

yama-taku.science

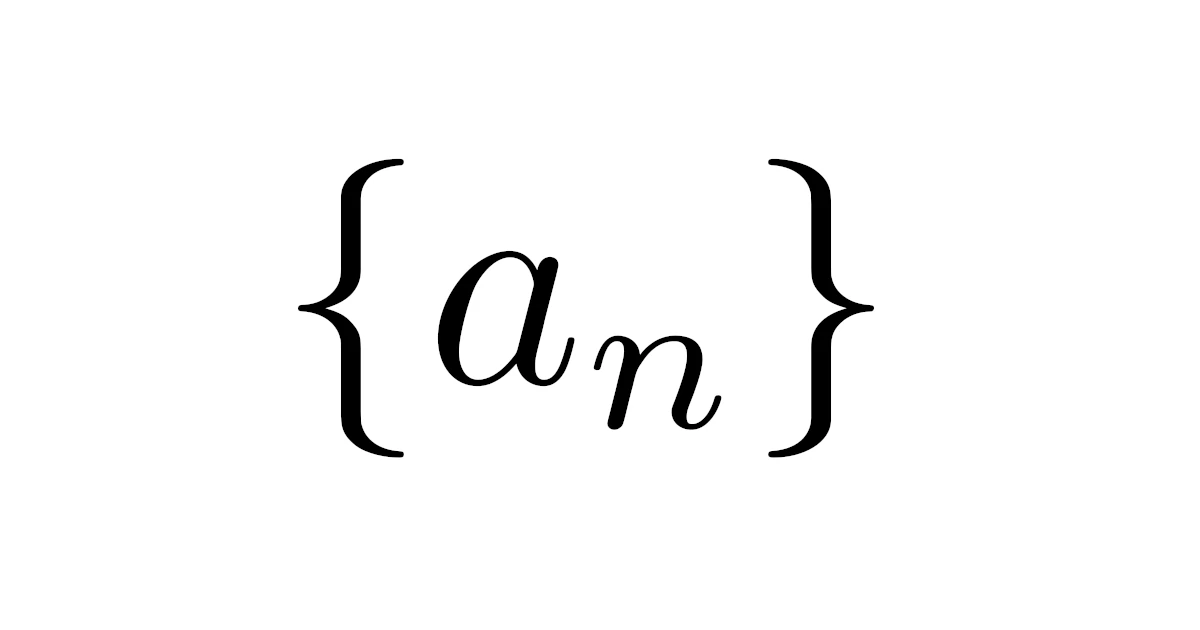
微分積分学

統計の計算では微分と積分を扱う場面がよくあります．

積分は高校数学の範囲で対応可能な部分がほとんどですが，微分は回帰分析などで偏微分を扱うことがあり，これは大学１年で学ぶ微分積分学の範囲です．

しかし，偏微分も普通の微分が分かっていればほとんど問題なく計算できますから，対症療法的に調べて進めることも可能でしょう．

良い点と気を付けたい点

本書の良い点と気になる点を挙げます．

良い点

• 統計の基礎的な項目が広く扱われているので，この一冊で統計の概観を掴むことができる．
• つまずきやすい序盤は具体例を多く用いて説明されているので，初学者にもイメージがしやすい．
• 現実的な統計の問題を例として扱っており，実践的な統計の扱いに触れることができる．
• 統計の２つの側面である「記述統計」と「推測統計」の違いに注意して書かれている．

気を付けたい点

• 統計の概観を広くさらう構成になっている反面，各項目が深くないのでこの１冊で理解しきるのが少々難しい．
• ある程度の計算力を前提としているため，高校数学が怪しい人には読み進めることが難しい．
• 練習問題が多くないので，本書のみで統計検定の試験問題が解けるようになるのは難しい．

全体の感想と使い方