剰余群の考え方｜well-definedの確認はなぜ必要か？

代数学
2019.04.23
代数学

代数学の群論の中でも剰余群はひとつの山場であり，定義の段階で既に戸惑ってしまう人は多いように思います．

剰余群の考え方の背景にはwell-defined性があり，これを知っていると比較的理解がしやすいでしょう．

逆に言えば，well-defined性の知識が欠けていると「どうしてこんな議論が必要なのか」と疑問に感じてしまい，スッキリ理解するのは難しいように思います．

この記事では

  • 可換群の剰余群
  • 一般の群の剰余群

の２段階に分けて，well-defined性の説明も交えながら剰余群を説明します．

可換群の剰余群

群は必ずしも可換ではありませんが，可換群の方が性質が良く理解しやすいので，まずは可換群の剰余群から説明します．

剰余群のイメージづくり

$G:=\Z$，$N:=3\Z$とします．このとき

  • $\Z$は整数の集合なので，$G$は通常の和$+$により可換群
  • $3\Z$は$\Z$の元を全て３倍した集合（つまり，３の倍数の集合）なので，$N$は$G$の部分群

となります．

群$G$の分解

このとき，集合として

    \begin{align*}G=N\cup(1+N)\cup(2+N)\end{align*}

となっていますね．ただし，$1+N$, $2+N$はそれぞれ

  • $1+N=\{\dots,-2,1,4,\dots\}$
  • $2+N=\{\dots,-1,2,5,\dots\}$

です．このとき，群$N$からできた３つの集合$N$, $1+N$, $2+N$の集合を$G/N$と表すことにします：

    \begin{align*}G/N=\{N,1+N,2+N\}.\end{align*}

$N$, $1+N$, $2+N$はいずれも集合なので，$G/N$は集合族（集合の集合）になっているということに注意してください．

$n+\N$の表し方

さて，ここでのポイントは，$N$の集合の元全てに

  • ３を足そうが
  • ６を足そうが
  • 12を足そうが

元がズレるだけで集合としては変わらないということです．つまり，

    \begin{align*}N=3+N=6+N=12+N\end{align*}

ということですね．同様に，たとえば

    \begin{align*}&1+N=4+N=-2+N, \\&2+N=11+N=-4+N\end{align*}

です．したがって，$G/N$は

    \begin{align*}G/N=\{3+N,-4+N,11+N\}\end{align*}

などとも表すことができるわけですね．

集合論的には$G/N=\{N,1+N,2+N\}$は商集合というものになっており，このとき$G/H$の１つ１つの元$N$, $1+N$, $2+N$を同値類と呼びます．

可換群の剰余群の定義

いま考えた$G/N$の例を一般化して，次のように可換群の剰余群を定義します．

［（可換群の）剰余群］演算$+$を備えた可換群$G$とその部分群$N$を考える．全ての$g\in G$に対して集合$g+N$を考え，それらの集合族を$G/N$と表す．

このとき，任意の$g_1,g_2\in G$に対して，$g_1+N,g_2+N\in G/N$の和$\dot{+}$を

    \begin{align*}(g_1+N)\dot{+}(g_2+N)=(g_1+g_2)+N\end{align*}

で定めると，$(G/N,\dot{+})$は可換群となる．この群$G/N$を剰余群（quotient group）といい，剰余群の元を剰余類という．

具体的に先ほど考えていた$G=\Z$, $N:=3\Z$の場合で，この剰余群の定義を当てはめて考えましょう．まず

    \begin{align*}\dots,-2+N,-1+N,N,1+N,2+N,\dots\end{align*}

と全ての$g+N$を考えます．

この中には$N=3+N=12+N$のように同じものがあるわけですが，このように同じものは１つとみなせば$N$, $1+N$, $2+N$の３つにまとめられます．

このようにしてできる集合族を$G/N$としているわけですね．

また，演算については

    \begin{align*}&(1+N)\dot{+}(1+N)=2+N, \\&(2+N)\dot{+}(3+N)=5+N, \\&(-2+N)\dot{+}(5+N)=3+N\end{align*}

という$G/N$の演算を定義すれば群になるということを述べているわけですね．

well-defined性の確認

ここで大切なことは剰余類$g_1+N$, $g_2+N$がどんな表し方をされていても，$(g_1+N)\dot{+}(g_2+N)$が同じ結果にならないといけないことです．

例えば$1+N=-2+N$と$3+N=9+N$ですから，$(1+N)\dot{+}(3+N)$と$(-2+N)\dot{+}(9+N)$は同じ結果になっていなければ困ります．

実際にこれらの和$\dot{+}$を計算すると，

    \begin{align*}&(1+N)\dot{+}(3+N)=4+N, \\&(-2+N)\dot{+}(9+N)=7+N\end{align*}

と確かに等しくなっているので，少なくともこの場合は問題なさそうです．

このように，剰余類$g_1+N$, $g_2+N$は複数の表し方がありうるので，どのような表し方をしても和$\dot{+}$の結果が同じになっていることは大切ですね．

この意味で剰余群の定義では演算のwell-defined性が重要になるわけですね．

剰余群の和$\dot{+}$の定義はwell-definedである．

$G/N$の任意の２元$g_1+N$, $g_2+N$を考え，これらはそれぞれ$h_1+N$, $h_2+N$とも書けるとする．

このとき，$(g_1+N)\dot{+}(g_2+N)=(g_1+g_2)+N$と$(h_1+N)\dot{+}(h_2+N)=(h_1+h_2)+N$が同じ結果になることを示せばよい．

$g_1+N=h_1+N$であることから$g_1-h_1\in N$が成り立ち，同様に$g_2-h_2\in N$が成り立つ．

$N$が群であることより

    \begin{align*}(g_1+g_2)-(h_1+h_2)=(g_1-h_1)+(g_2-h_2)\in\N\end{align*}

だから，$(g_1+g_2)+N=(h_1+h_2)+N$となり，確かに両者が等しいことが分かった．

これで可換群の剰余類の和がwell-definedであることが確かめられました．

一般の剰余群

次に可換とは限らない群に関して，剰余群を考えます．

正規部分群

結論から先に言えば，一般の剰余群$G/N$を考えるためには$N$が正規部分群であることが必要です．

群$G$の部分群$N$が$G$の正規部分群（normal subgroup）であるとは，任意の$g\in G$と$h\in N$に対して

    \begin{align*}ghg^{-1}\in N\end{align*}

が成り立つことをいう．

例えば，$G$が可換群なら

    \begin{align*}ghg^{-1}=gg^{-1}h=h\in N\end{align*}

となるので，可換群の任意の部分群は正規部分群となります．

そのため，先ほど考えた可換群の剰余群では正規部分群を持ち出さなくても問題なく議論できたわけですね．

剰余群の定義

一般の群$G$とその部分群$N$に対して，$N$が正規部分群なら剰余類$G/H$は群となります．

［（一般の群の）剰余群］群$G$とその正規部分群$N$を考える．全ての$g\in G$に対して集合$gN$を考え，$gN$たちで同じもの集合を１つとしてできる集合族を$G/N$と表す．

任意の$g_1,g_2\in G$に対して，$g_1N,g_2N\in G/N$の積を

    \begin{align*}(g_1N)(g_2N)=(g_1g_2)N\end{align*}

で定めると，$G/N$は群となる．この群$G/N$を剰余群（quotient group）という．

可換とは限らない一般の群$G$の剰余群$G/N$を考える際には，必ず$N$は正規でなければなりません．

それでは，この一般の剰余群の定義について，well-defined性を証明します．

任意の$G/N$の２元$g_1N=h_1N$と$g_2N=h_2N$を考える．

    \begin{align*}g_1{h_1}^{-1},g_2{h_2}^{-1}\in N\end{align*}

なので，$n_1,n_2\in N$が存在して，$n_1=g_1{h_1}^{-1}$, $n_2=g_2{h_2}^{-1}$が成り立つ．よって，

    \begin{align*}&g_1g_2(h_1h_2)^{-1} \\=&g_1g_2{h_2}^{-1}{h_1}^{-1} \\=&(n_1h_1)(n_2h_2){h_2}^{-1}{h_1}^{-1} \\=&n_1(h_1n_2{h_1}^{-1})\end{align*}

が成り立つ．いま，$n_1\in N$であり，$N$は$G$の正規部分群だから$h_1n_2{h_1}^{-1}\in N$である．

よって，$n_1(h_1n_2{h_1}^{-1})\in N$だから$g_1g_2(h_1h_2)^{-1}\in N$が得られ，$(g_1g_2)N=(h_1h_2)N$が成り立つ．

以上より，$(g_1N)(g_2N)=(h_1N)(h_2N)$となって，well-defined性が従う．

参考文献

以下は参考文献です．

代数学１ 群論入門

[雪江明彦 著/日本評論社]

本書は群論の入門書です．また，続巻として

  • 第２巻「環と体とガロア理論」
  • 第３巻「代数学のひろがり」

があります．

代数学は抽象的な分野と言われますが，抽象を理解するためには具体の理解が大切なことも多いです．

本書は具体例が多く扱われており，初学者にも読み進めやすい良著です．さらに，章末問題は基本問題から少し考える問題まで様々なレベルのものがあります．

また読むために必要な基礎事項を第１章にまとめてあり，予備知識をあまり仮定せずに独学で学びやすいのも嬉しい点です．

なお，本書については，以下の記事で書評としてまとめています．

【オススメの教科書｜代数学１ 群論入門(雪江明彦著，日本評論社)】

本書の目次・必要な知識・良い点と気になる点・オススメの使い方などをレビューしています．

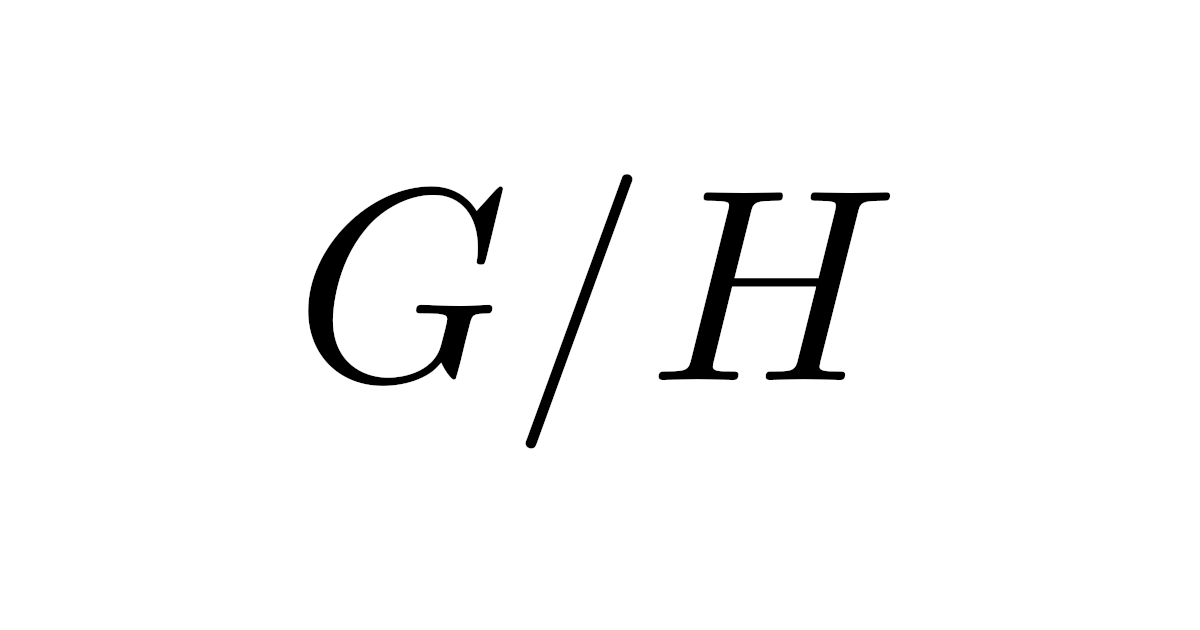
コメント