大学理系学部の多くの1年生が学ぶ微分積分学では
\begin{align*}f:\R\to\R;x\mapsto x^{2}\end{align*}
のような実変数の実数値関数の微分積分を考えます.学年が進むと
\begin{align*}f:\C\to\C;z\mapsto z^{2}\end{align*}
のような複素関数(複素変数の複素数値関数)の微分積分を考えるようになり,複素関数の微分積分を考える分野を複素解析学や関数論などといいます.
もともと複素解析学は実数の微分積分に応用するために研究されていた側面があり,この一連の記事では実数の微分積分への重要な応用がある留数定理を目標として説明していきます.
この記事では
- 複素関数の定義と図示の仕方
- 複素関数の具体例
を順に解説します.
「複素解析の基本」の一連の記事
複素関数の定義と図示の仕方
まずは複素関数の主役である複素関数を定義し,複素関数の図示の方法を説明します.
複素関数とは複素数を与えて複素数を返す関数
複素変数の複素数値関数を複素関数という.
冒頭で紹介した関数
\begin{align*}f:\C\to\C;z\mapsto z^{2}\end{align*}
も複素関数ですね.定義域は必ずしも複素数全体$\C$である必要はなく,
\begin{align*}f:\C\setminus\{i,-i\}\to\C;z\mapsto \frac{1}{z+i}+\frac{1}{z-i}\end{align*}
も複素関数です.
一般に集合$A$, $B$に対して$A\setminus B$は$A$から$B$を除いた集合$A\cap B^c$を表します.よって,$\C\setminus\{i,-i\}$は複素数全体から$\pm i$を除いた集合を表します.
複素関数のグラフは2枚の複素平面を使って描ける
実変数の実数値関数は変数の軸$\R$と返ってくる値の軸$\R$の2本を用いて1枚の図でグラフを描けるのでした.例えば,
\begin{align*}f:\R\to\R;x\mapsto x^{2}\end{align*}
は次のように図示できますね.
一方,複素関数を図示するには変数の複素平面$\C$と返ってくる値の複素平面$\C$が必要なので,1枚の図でグラフを描くには4次元必要となるので手書きではかなり困難です.
そこで複素関数を図示するには2枚の複素平面を並べて用います.
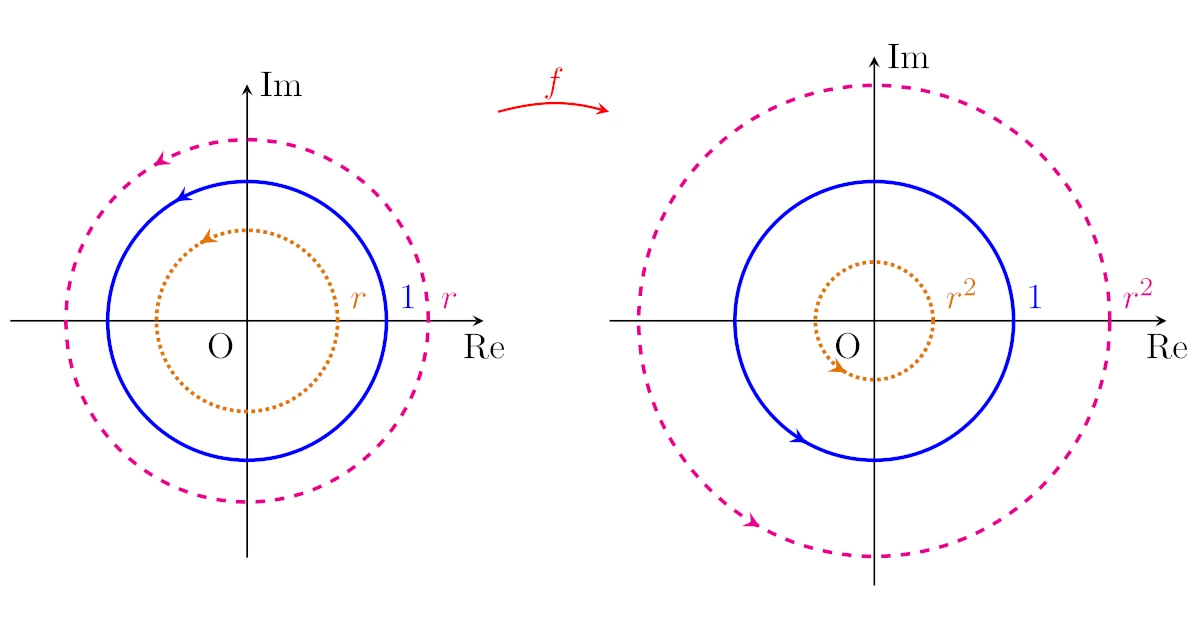
2枚の複素平面を用いて,複素関数$f:\C\to\C;z\mapsto z^{2}$を図示せよ.
冪(指数)の計算は極形式で考えるのが鉄板ですね.
そこで,例えば$z=\sqrt{2}(\cos{60^\circ}+i\sin{60^\circ})$なら,ド・モアルブルの定理より
\begin{align*}f(z)=&\brb{\sqrt{2}(\cos{60^\circ}+i\sin{60^\circ})}^2
\\=&2(\cos{120^\circ}+i\sin{120^\circ})\end{align*}
なので,これは以下のように図示できます.
つまり,ド・モアブルの定理から偏角は2倍されます.
また,この例では$z$の絶対値$\sqrt{2}$が1より大きいので$z^2$の絶対値はより大きくなりますが,$z$の絶対値$\sqrt{2}$が1より小さい場合には$z^2$の絶対値はより小さくなりますね.
このことから,以下のように解答が書けることが分かります.
原点中心,半径$r$の円周を$C_{r}$とします.
$z\in C_{r}$は$z=r(\cos{\theta}+i\sin{\theta})$($r\ge0$, $0\le\theta<2\pi$)と極形式で表すことができるので,ド・モアブルの定理より
\begin{align*}f(z)=r^{2}(\cos{2\theta}+i\sin{2\theta})\end{align*}
となるから,$z$が$C_r$上を1周するとき,$f(z)$は$C_{r^2}$上を2周することが分かりますね.
図中の矢印の位置と向きも対応していることに注意してください.
複素関数の具体例
他にもいくつか複素関数を図示してみましょう.
例1($f(z)=\overline{z}$)
2枚の複素平面を用いて,複素関数$f:\C\to\C;z\mapsto\overline{z}$を図示せよ.
$z\in\C$とその共役$\overline{z}$は複素平面上で実軸対称な点を表しますから,下図のようになりますね.
この他にもさまざまな図示が考えられます.例えば,下図のように図示してもよいですね.
例2($f(z)=\alpha z+i$)
$\alpha=s(\cos{\phi}+i\sin{\phi})$($s>0$, $\phi\in\R$)とする.2枚の複素平面を用いて,複素関数$f:\C\to\C;z\mapsto\alpha z+i$を図示せよ.
原点中心,半径$r$の円周を$C_{r}$とします.
$z\in C_{r}$は$z=r(\cos{\theta}+i\sin{\theta})$ ($r\ge0$, $\theta\in\R$)と極形式で表すことができ,
\begin{align*}g(z)=rs(\cos{(\theta+\phi)}+i\sin{(\theta+\phi)})+i\end{align*}
となりますから,$g$は$C_{r}$を原点中心に$s$倍に拡大,$+\phi$回転し,虚軸方向に$+1$平行移動させた円に移しますね.


コメント