物理学の量子力学で最初に考案された「ディラックのデルタ関数」は,当初は数学的には厳密ではなく「形式的な関数」として登場しました.
ローラン・シュワルツ(Laurent Schwartz)氏は「ディラックのデルタ関数」のようなものも含む超関数の枠組みを数学的に厳密に整備し,1950年にフィールズ賞を受賞しました.
現代では超関数は解析学で広く使われる概念となっており,例えば実数階ソボレフ空間など多くの関数空間の基礎となっています.
この記事では
- 急減少関数と緩増加超関数の定義
- 局所可積分関数と緩増加超関数
- 緩増加超関数の具体例(デルタ関数,コーシーの主値)
を順に解説します.
この記事で扱う緩増加超関数は最初にローラン-シュワルツが整備した超関数とは少々異なるものですが,現代の解析学では最もよく用いられている超関数です.
急減少関数と緩増加超関数の定義
急減少関数の定義を確認し,本題の緩増加超関数を定義しましょう.
多重指数を用いた偏導関数と冪の表し方
まずは偏微分を表す際に便利な多重指数を定義します.
非負整数$\alpha_1,\alpha_2,\dots,\alpha_n$の組$\alpha:=(\alpha_1,\alpha_2,\dots,\alpha_n)$を多重指数という.また,成分の和$\alpha_1+\alpha_2+\dots+\alpha_n$を$|\alpha|$と表す.
$n$成分の多重指数全部の集合は,非負整数全部の集合$\N_{\ge0}$の直積として$\N_{\ge0}^n$などと表すこともよくあります.
開集合$A\subset\R^n$と,関数$f:A\to\R$を考える.多重指数$\alpha=(\alpha_1,\alpha_2,\dots,\alpha_n)$に対して,偏導関数
\begin{align*}\frac{\partial^{|\alpha|} f}{\partial x_1^{\alpha_1}\partial x_2^{\alpha_2}\dots\partial x_n^{\alpha_n}}\end{align*}
を$\partial^{\alpha}f$や$D^{\alpha}f$などと表す.
例えば,3変数関数$f$と多重指数$\alpha=(2,3,0)$に対しては$\partial^{\alpha}f(x,y,z)=\frac{\partial^{5} f}{\partial x^2\partial y^{3}}(x,y,z)$ということですね.
急減少関数は微分しても多項式をかけても遠方で減衰する関数
関数$f\in C^\infty(\R^n)$が急減少関数(rapidly decreasing function)であるとは,任意の$m\in\N_{\ge0}$に対して
\begin{align*}\|f\|_{m}:=\sum_{|\alpha|+k\le m}\sup_{x\in\R^n}\abs{(1+|x|^2)^{k}\partial^{\alpha}f(x)}<\infty\end{align*}
が成り立つことをいう.ただし,$\alpha\in\N_{\ge0}^{n}$, $k\in\N_{\ge0}$である.
$\R^n$上の急減少関数全部の集合を$\mathcal{S}(\R^n)$や単に$\mathcal{S}$と表し,$\mathcal{S}(\R^n)$は通常の和と積により線形空間となります.この空間シュワルツ空間(Schwartz space)といいます:
\begin{align*}\mathcal{S}=\mathcal{S}(\R^n):=\set{f\in C^\infty(\R^n)}{\forall m\in\N_{\ge0}\quad\|f\|_{m}<\infty}\end{align*}
シュワルツ空間は(フレシェ空間として)完備距離空間となりますが,その証明は以下の記事を参照してください.

緩増加超関数はシュワルツ空間の有界線形汎関数
写像$T:\mathcal{S}(\R^n)\to\C$が緩増加超関数であるとは,次の2条件を同時に満たすことをいう.
- [線形性]任意の$f,g\in\mathcal{S}(\R^n)$, $k\in\C$に対して,$T(kf+g)=kTf+Tg$が成り立つ.
- [有界性]ある$C>0$と$m\in\N_{\ge0}$が存在して,任意の$f\in\mathcal{S}(\R^n)$に対して,$|Tf|\le C\|f\|_{m}$が成り立つ.
一般に,線形空間の元に対して$\R$や$\C$の元を対応させる関数のことを汎関数(functional)といいます.よって,以上の定義は「シュワルツ空間$\mathcal{S}(\R^n)$の有界線形汎関数を緩増加超関数という」と短く表現できますね.
また,一般に線形空間$V$上の有界線形汎関数全部の集合を$V^*$などと表し,$V$の双対空間(dual space)や共役空間(conjugate space)といいます.よって,$\R^n$上の緩増加超関数全部の集合は$\mathcal{S}^*(\R^n)$や単に$\mathcal{S}^*$と表します.
また,$Tf$のことを$\anb{T,f}$とカップリングで表すこともよくあります.
一般に線形汎関数に対しては,有界性と連続性(任意の$\alpha,\beta\in\N_{\ge0}^{n}$に対して$\|f_n\|_{\alpha,\beta}\to0$なら$Tf_n\to0$が成り立つ)は同値なので,テキストによっては定義の有界性が連続性に置き換わっていることもあります.
局所可積分関数と緩増加超関数
緩増加超関数はたかだか多項式増大する局所可積分関数の拡張と捉えることができます.
局所可積分関数は任意の有界閉集合上で可積分な関数
関数$f:\R^n\to\R$が局所可積分であるとは,任意の有界閉集合$K\subset\R^n$上で$f$が可積分であることをいい,$\R^n$上の局所可積分関数全部の空間を$L^1_\text{loc}(\R^n)$などと表す.
例えば,$\R^n$上の連続関数,$p$乗可積分関数は局所可積分関数です.
$p\in[1,\infty]$とする.$C(\R^n)\subset L^1_\text{loc}(\R^n)$, $L^p(\R^n)\subset L^1_\text{loc}(\R^n)$が成り立つ.
$C(\R^n)\subset L^1_\text{loc}(\R^n)$の証明
任意に$f\in C(\R^n)$をとる.任意の有界閉集合$K$に対して,$M:=\sup\limits_{x\in K}|f(x)|<\infty$なので,
\begin{align*}\int_{K}|f(x)|\,dx\le\int_{K}M\,dx=M|K|<\infty\end{align*}
だから,$f$は$K$上可積分である.よって,$f\in L^1_\text{loc}(\R^n)$である.
$L^p(\R^n)\subset L^1_\text{loc}(\R^n)$の証明
任意に$f\in L^p(\R^n)$をとる.任意の有界閉集合$K$に対して,ヘルダーの不等式より
\begin{align*}\int_{K}|f(x)|\,dx&\le\bra{\int_{K}1^q\,dx}^{1/q}{\int_{K}|f(x)|^p\,dx}^{1/p}
\\&=|K|^{1/q}{\int_{K}|f(x)|^p\,dx}^{1/p}<\infty\end{align*}
だから,$f$は$K$上可積分である.よって,$f\in L^1_\text{loc}(\R^n)$である.
たかだか多項式増大の$\phi\in L^1_\text{loc}(\R^n)$から緩増加超関数$T_{\phi}$をつくる
たかだか多項式増大の局所可積分関数は次の意味で緩増加超関数とみなすことができます.
$\phi\in L^1_\text{loc}(\R^n)$を考える.ある$p\in\N_{\ge0}$と$C>0$が存在して,任意の$x\in\R^n$に対して,$\phi(x)\le C(1+|x|)^p$が成り立つとき,
\begin{align*}T_{\phi}(f)=\int_{\R^n}\phi(x)f(x)\,dx\quad(f\in\mathcal{S}(\R^n))\end{align*}
で定まる汎関数$T_{\phi}:\mathcal{S}(\R^n)\to\R$は緩増加超関数である.
$\phi(x)f(x)$が可積分であることの証明
任意に$f\in\mathcal{S}(\R^n)$をとる.ある$p\in\N_{\ge0}$と$C>0$が存在して,任意の$x\in\R^n$に対して,$\phi(x)\le C(1+|x|)^p$が成り立つことに注意して,
\begin{align*}|\phi(x)f(x)|&\le C(1+|x|)^p|f(x)|
\\&=C(1+|x|)^{-n-1}(1+|x|)^{p+n+1}|f(x)|\end{align*}
となる.ここで,$p+n+1<2m$となる$m\in\N$をとれば,任意の$x\in\R^n$に対して
\begin{align*}(1+|x|)^{p+n+1}&\le(1+|x|)^{2m}=(1+2|x|+|x|^2)^{m}
\\&\le(1+2(1+|x|^2)+|x|^2)^{m}\le3^m(1+|x|^2)^m\end{align*}
となるから,$I:=\int_{\R^n}(1+|x|)^{-n-1}\,dx<\infty$と併せて
\begin{align*}&\int_{\R^n}|\phi(x)||f(x)|\,dx
\\&\le3^mC\int_{\R^n}(1+|x|)^{-n-1}(1+|x|^2)^m|f(x)|\,dx
\\&\le3^mCI\|f\|_{m}\end{align*}
となり,$\int_{\R^n}\phi(x)f(x)\,dx<\infty$である.よって,$T_{\phi}$は汎関数である.
線形性の証明
任意の$f,g\in\mathcal{S}(\R^n)$, $k\in\C$に対して,
\begin{align*}&T_{\phi}(kf+g)=\int_{\R^n}\phi(x)(kf(x)+g(x))\,dx
\\&=k\int_{\R^n}\phi(x)f(x)\,dx+\int_{\R^n}\phi(x)g(x)\,dx
\\&=kT_{\phi}(f)+T_{\phi}(g)\end{align*}
が成り立つ.よって,$T_{\phi}$は線形である.
有界性の証明
任意に$f\in\mathcal{S}(\R^n)$をとる.積分が有限の値であることの証明と同様に,ある$p\in\N_{\ge0}$と$C>0$が存在して,任意の$x\in\R^n$に対して,
\begin{align*}|T_{\phi}f(x)|&=\abs{\int_{\R^n}\phi(x)f(x)\,dx}
\\&\le\int_{\R^n}|\phi(x)||f(x)|\,dx
\\&\le3^mCI\|f\|_{m}\end{align*}
となり,$T_{\phi}$は有界である.
$\phi\in L^1_{\text{loc}}(\R^n)$が異なれば緩増加超関数$T_{\phi}$も異なる
異なる$\phi\in L^1_{\text{loc}}(\R^n)$に対しては$T_\phi$も異なるものになります.
[変分法の基本補題]$f\in L^1_{\text{loc}}(\R^n)$とする.任意の$\phi\in C_0^{\infty}(\R^n)$に対して
\begin{align*}\int_{\R^n}f(x)\phi(x)\,dx=0\end{align*}
が成り立てば,$\R^n$上ほとんど至るところ$f=0$が成り立つ.
ここでは,この補題を認めて次を証明しましょう.
たかだか多項式増大の$\phi,\psi\in L^1_{\text{loc}}(\R^n)$とする.$T_\phi=T_\psi$が成り立てば,$\R^n$上ほとんど至るところ$\phi=\psi$が成り立つ.
$T_\phi=T_\psi$より,任意の$f\in\mathcal{S}(\R^n)$に対して,$T_\phi(f)=T_\psi(f)$だから
\begin{align*}\int_{\R^n}(\phi(x)-\psi(x))f(x)\,dx=0\end{align*}
が成り立つから,変分法の基本補題よりほとんど至るところ$\phi-\psi=0\iff\phi=\psi$が成り立つ.
この命題より,緩増加超関数全部の空間$\mathcal{S}^*(\R^n)$は局所可積分関数全部の空間$L^1_{\text{loc}}(\R^n)$の拡張であると捉えることができますね.
緩増加超関数の具体例(デルタ関数,コーシーの主値)
具体例1(ディラックのデルタ関数$\delta_a$)
$a\in\R^n$とする.
\begin{align*}\delta_a(f)=f(a)\quad(f\in\mathcal{S}(\R^n))\end{align*}
で定まる汎関数$\delta_a:\mathcal{S}(\R^n)\to\R$を$a$におけるディラックのデルタ関数という.
例えば,$f(x)=e^{-x^2}$で定まる$f\in\mathcal{S}(\R)$に対して,
\begin{align*}\delta_0(f)=f(0)=e^{-0^2}=1\end{align*}
となります.このように,放り込んだ関数$f\in\mathcal{S}(\R^n)$の$a\in\R^n$での値$f(a)$を返す汎関数がディラックのデルタ関数というわけですね.
$a\in\R^n$とする.$a$におけるディラックのデルタ関数$\delta_a$は緩増加超関数である.
$\delta_a$は$\mathcal{S}(\R^n)$上の汎関数である.あとは線形性と有界性を示せばよい.
線形性の証明
任意の$f,g\in\mathcal{S}(\R^n)$, $k\in\C$に対して,
\begin{align*}\delta_a(kf+g)
&=(kf+g)(a)
\\&=kf(a)+g(a)
\\&=k\delta_a(f)+\delta_a(g)\end{align*}
が成り立つ.よって,$\delta_a$は線形である.
有界性の証明
任意の$f\in\mathcal{S}(\R^n)$に対して,
\begin{align*}|\delta_a(f)|=|f(a)|\le\|f\|_0\end{align*}
となり,$\delta_a$は有界である.
このディラックのデルタ関数$\delta_a$($a\in\R^n$)はどんな$\phi\in L^1_{\text{loc}}(\R^n)$を用いても,$\phi\in L^1_{\text{loc}}$による緩増加超関数$T_\phi$で表せません.
そのため,ディラックのデルタ関数$\delta_a$は$\phi\in L^1_{\text{loc}}(\R^n)$から真に拡張された超関数ということができます.
具体例2(コーシーの主値)
$f\in\mathcal{S}(\R)$に対して,
\begin{align*}T(f)=\lim_{\epsilon\to+0}\frac{1}{\pi}\bra{\int_{-\infty}^{-\epsilon}\frac{f(x)}{x}\,dx+\int_{\epsilon}^{\infty}\frac{f(x)}{x}\,dx}\end{align*}
で定まる汎関数$T:\mathcal{S}(\R)\to\R$を考えます.
被積分関数は0で特異点をもちますが,$f$が0で連続であることより$\epsilon>0$が十分小さいとき$\frac{f(\epsilon)}{\epsilon}\approx\frac{f(-\epsilon)}{\epsilon}$だから打ち消し合い,積分は有限の値となります.
このように,特異点から対称的に積分範囲を除いて積分し,その極限で定義する積分の値をコーシーの主値(principal value)といい,いまの場合は
\begin{align*}T(f)=\frac{1}{\pi}\text{p.v.}\int_{-\infty}^{\infty}\frac{f(x)}{x}\,dx\end{align*}
とも表せます.
$f\in\mathcal{S}(\R)$に対して,
\begin{align*}T(f)=\lim_{\epsilon\to+0}\frac{1}{\pi}\bra{\int_{-\infty}^{-\epsilon}\frac{f(x)}{x}\,dx+\int_{\epsilon}^{\infty}\frac{f(x)}{x}\,dx}\end{align*}
で定まる汎関数$T:\mathcal{S}(\R)\to\R$は緩増加超関数である.
$\frac{f(x)}{x}$がコーシーの主値をもつことの証明
任意に$f\in\mathcal{S}(\R)$をとる.$x\to\infty$では$f(x)=o(\frac{1}{x})$なので,原点での特異性を考えればよい.
\begin{align*}&\text{p.v.}\int_{-1}^{1}\frac{f(x)}{x}\,dx
\\&=\text{p.v.}\int_{-1}^{1}\frac{f(x)-f(0)}{x}\,dx+\text{p.v.}\int_{-1}^{1}\frac{f(0)}{x}\,dx\end{align*}
である.平均値の定理より,任意の$x\in(-1,1)\setminus\{0\}$に対して,$x$と0の間のある値$c_x$が存在して,$f(x)-f(0)=xf'(c_x)$が成り立つから,第1項目について
\begin{align*}&\text{p.v.}\int_{-1}^{1}\frac{f(x)-f(0)}{x}\,dx
\\&=\text{p.v.}\int_{-1}^{1}f'(c_x)\,dx\le\text{p.v.}\int_{-1}^{1}\|f\|_{1}\,dx=2\|f\|_1\end{align*}
が成り立つ.第2項目について
\begin{align*}&\text{p.v.}\int_{-1}^{1}\frac{f(0)}{x}\,dx
\\&=\lim_{\epsilon\to+0}\bra{\int_{-1}^{-\epsilon}\frac{f(0)}{x}\,dx+\int_{\epsilon}^{1}\frac{f(0)}{x}\,dx}
\\&=\lim_{\epsilon\to+0}f(0)(\log{|-\epsilon|}-\log{|\epsilon|})=0\end{align*}
が成り立つ.よって,$T$は汎関数$\mathcal{S}(\R)\to\R$である.
線形性の証明
任意の$f,g\in\mathcal{S}(\R)$, $k\in\C$に対して,
\begin{align*}T(kf+g)&=\frac{1}{\pi}\text{p.v.}\int_{-\infty}^{\infty}\frac{(kf+g)(x)}{x}\,dx
\\&=\frac{k}{\pi}\text{p.v.}\int_{-\infty}^{\infty}\frac{f(x)}{x}\,dx+\frac{1}{\pi}\text{p.v.}\int_{-\infty}^{\infty}\frac{g(x)}{x}\,dx
\\&=kT(f)+T(g)\end{align*}
が成り立つ.よって,$T$は線形である.
有界性の証明
任意に$f\in\mathcal{S}(\R)$をとる.
\begin{align*}T(f)=\int_{|x|\ge1}\frac{f(x)}{x}\,dx+\text{p.v.}\int_{-1}^{1}\frac{f(x)}{x}\,dx\end{align*}
である.第1項目について
\begin{align*}\int_{|x|\ge1}\frac{f(x)}{x}\,dx
&=2\int_{1}^{\infty}\frac{xf(x)}{x^2}\,dx
\\&\le2\int_{1}^{\infty}\frac{\|f\|_1}{x^2}\,dx=\|f\|_1\end{align*}
が成り立ち,第2項目について積分が有限の値であることの証明より
\begin{align*}&\text{p.v.}\int_{-1}^{1}\frac{f(x)}{x}\,dx\le2\|f\|_1\end{align*}
が成り立つ.よって,$|T(f)|\le3\|f\|_1$となり$T$は有界である.

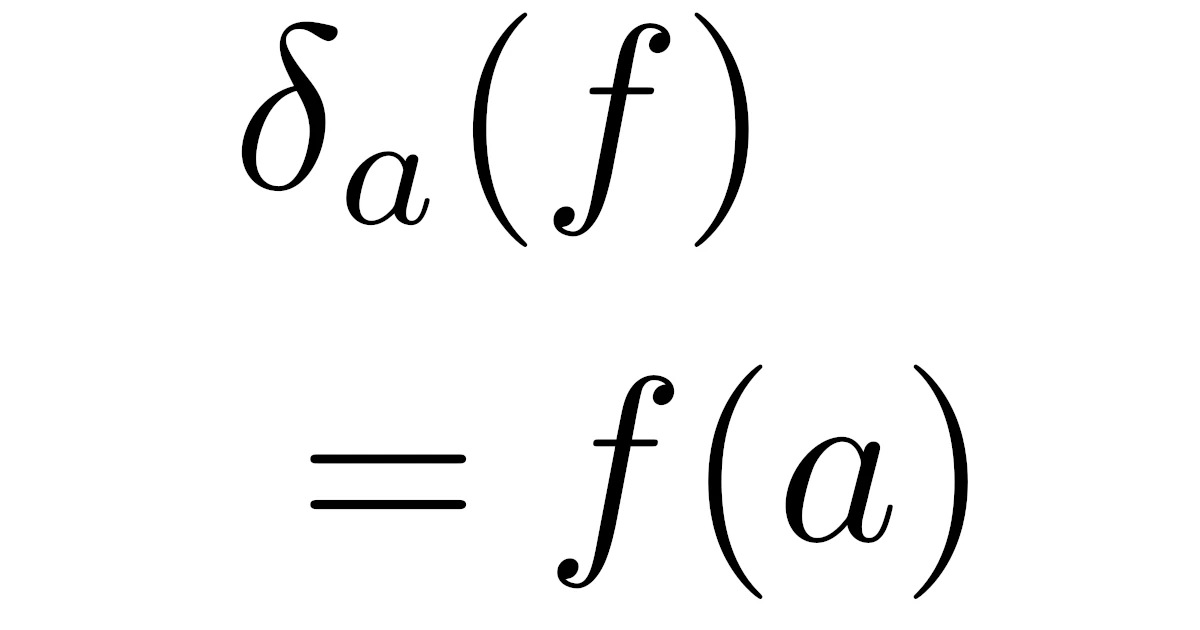
コメント