ベクトル解析において,3つの微分作用素
- 勾配$\operatorname{grad}$
- 発散$\operatorname{div}$
- 回転$\operatorname{rot}$ ($\operatorname{curl}$)
は基本的で,多くの場面で現れます.
とくに積に関する微分(例えば$\operatorname{div}{f\m{v}}$, $\operatorname{grad}(fg)$など)はよく現れ,これは公式として当たり前に使えるようになっておきたいところです.
この記事では,これら3つの基本の微分作用素の
- 和の微分公式
- 積の微分公式
- 内積/外積の微分公式
をまとめます.
なお,勾配$\operatorname{grad}$,発散$\operatorname{div}$,回転$\operatorname{rot}$の定義とイメージについては以下の記事を参照してください.
3つの微分作用素の確認
この記事では
- 第$i$変数$x_i$に関する偏微分を$\partial_{i}$
- 3変数$\m{x}=\bmat{x\\y\\z}$の場合には,$x,y,z$に関する偏微分をそれぞれ$\partial_x,\partial_y,\partial_z$
で表します.
これらは解析ではよく用いられる略記です.
勾配$\operatorname{grad}$,発散$\operatorname{div}$,回転$\operatorname{rot}$の定義を確認しておきましょう.大事なことは
- 勾配$\operatorname{grad}$は関数$f:\R^n\to\R$に
- 発散$\operatorname{div}$はベクトル値関数$\m{v}:\R^n\to\R^n$に
- 回転$\operatorname{rot}$はベクトル値関数$\m{v}:\R^3\to\R^3$に
対して定義されるという点です.
各変数について偏微分可能な関数$f:\R^n\to\R$に対して,
\begin{align*}\operatorname{grad}f:=\bmat{\partial_{1}f\\\vdots\\\partial_{n}f}\end{align*}
で$\operatorname{grad}f:\R^n\to\R^n$を定め,これを$f$の勾配 (gradient)という.
各変数について偏微分可能なベクトル値関数$\m{v}:\R^n\to\R^n$に対して,
\begin{align*}\operatorname{div}\m{v}:=\sum_{i=1}^{n}\partial_{i}v_i\end{align*}
で$\operatorname{div}\m{v}:\R^n\to\R$を定め,これを$\m{v}$の発散 (divergence)という.
各変数について偏微分可能なベクトル値関数$\m{v}:\R^3\to\R^3$に対して,
\begin{align*}\operatorname{rot}\m{v}:=\bmat{\partial_{y}w-\partial_{z}v\\\partial_{z}u-\partial_{x}w\\\partial_{x}x-\partial_{y}u}\end{align*}
で$\operatorname{rot}\m{v}:\R^3\to\R^3$を定め,これを$\m{v}$の回転 (rotation,curl)という.$\operatorname{rot}\m{v}$は$\operatorname{curl}\m{v}$と表すこともある.
ナブラ(nabla)$\nabla:=\bmat{\partial_1\\\vdots\\\partial_n}$を使うと,
\begin{align*}\operatorname{grad}f=\nabla f,\quad
\operatorname{div}\m{v}=\nabla\cdot\m{v},\quad
\operatorname{rot}\m{v}=\nabla\times\m{v}\end{align*}
と(形式的に)表せるのでしたね.この記法について詳しくは以下の記事を参照してください.

gradとdivとrotの公式
以下では,$\operatorname{rot}$が関係する公式では3次元で考え,$\operatorname{rot}$が関係しない公式では任意の次元$n$で考えます.
また,
- 関数を$f,g:\R^n\to\R$
- ベクトル値関数を$\m{u}=\bmat{u_1\\\vdots\\u_n},\m{v}=\bmat{v_1\\\vdots\\v_n}:\R^n\to\R^n$
とします.
和・定数倍の微分公式
和の微分について,以下が成り立ちます.
関数$f,g:\R^n\to\R$と定数$\alpha,\beta\in\R$に対して,以下が成り立つ.
- $\operatorname{grad}(\alpha f+\beta g)=\alpha\operatorname{grad}f+\beta\operatorname{grad}g$
- $\operatorname{div}(\alpha \m{u}+\beta\m{v})=\alpha\operatorname{div}\m{u}+\beta\operatorname{div}\m{v}$
- $\operatorname{rot}(\alpha \m{u}+\beta\m{v})=\alpha\operatorname{rot}\m{u}+\beta\operatorname{rot}\m{v}$
[$\operatorname{grad}$について] $\operatorname{grad}(\alpha f+\beta g)$の第$i$成分は
\begin{align*}\partial_{i}(\alpha f+\beta g)
=\alpha\partial_{i}f+\beta\partial_{i}g\end{align*}
となり,これは$\alpha\operatorname{grad}f+\beta\operatorname{grad}g$の第$i$成分に等しい($i=1,2,\dots,n$).
よって,$\operatorname{grad}(\alpha f+\beta g)=\alpha\operatorname{grad}f+\beta\operatorname{grad}g$が成り立つ.
[$\operatorname{div}$について]
\begin{align*}
\operatorname{div}(\alpha\m{u}+\beta\m{v})
=&\sum_{i=1}^{n}\partial_i(\alpha u_i+\beta v_i)
\\=&\sum_{i=1}^{n}(\alpha\partial_{i}u_i+\beta\partial_{i}v_i)
\\=&\alpha\sum_{i=1}^{n}\partial_{i}u_i+\beta\sum_{i=1}^{n}\partial_{i}v_i
\\=&\alpha\operatorname{div}\m{u}+\beta\operatorname{div}\m{v}
\end{align*}
が成り立つ.
[$\operatorname{rot}$について]
\begin{align*}
\operatorname{rot}(\alpha\m{u}+\beta\m{v})
=&\bmat{\partial_y(\alpha u_3+\beta v_3)-\partial_z(\alpha u_2+\beta v_2)\\
\partial_z(\alpha u_1+\beta v_1)-\partial_x(\alpha u_3+\beta v_3)\\
\partial_x(\alpha u_2+\beta v_2)-\partial_y(\alpha u_1+\beta v_1)}
\\=&\bmat{\bra{\alpha\partial_{y}u_3+\beta\partial_{y}v_3}-\bra{\alpha\partial_{z}u_2+\beta\partial_{z}v_2}\\
\bra{\alpha\partial_{z}u_1+\beta\partial_{z}v_1}-\bra{\alpha\partial_{x}u_3+\beta\partial_{x}v_3}\\
\bra{\alpha\partial_{x}u_2+\beta\partial_{x}v_2}-\bra{\alpha\partial_{y}u_1+\beta\partial_{y}v_1}}
\\=&\alpha\bmat{\partial_{y}u_3-\partial_{z}u_2\\\partial_{z}u_1-\partial_{x}u_3\\\partial_{x}u_2-\partial_{y}u_1}
+\beta\bmat{\partial_{y}v_3-\partial_{z}v_2\\\partial_{z}v_1-\partial_{x}v_3\\\partial_{x}v_2-\partial_{y}v_1}
\\=&\alpha\operatorname{rot}\m{u}+\beta\operatorname{rot}\m{v}
\end{align*}
が成り立つ.
いずれも$\partial_i$ $(i=1,\dots,n)$の線形性から,同様に導かれていますね.
積の微分公式
関数$f,g:\R^n\to\R$とベクトル値関数$\m{v}:\R^n\to\R^n$に対して,
- $fg:\R^n\to\R$
- $f\m{v}=\bmat{fv_1\\\vdots\\fv_n}:\R^n\to\R^n$
となっていることに注意して下さい.これらについて,以下が成り立ちます.
関数$f,g:\R^n\to\R$とベクトル値関数$\m{v}:\R^n\to\R^n$に対して,以下が成り立つ.
- $\operatorname{grad}(fg)=(\operatorname{grad}f)g+f(\operatorname{grad}g)$
- $\operatorname{div}(f\m{v})=(\operatorname{grad}f)\cdot\m{v}+f(\operatorname{div}\m{v})$
- $\operatorname{rot}(f\m{v})=(\operatorname{grad}f)\times\m{v}+f(\operatorname{rot}\m{v})$
[$\operatorname{grad}$について] $\operatorname{grad}(fg)$の第$i$成分は
\begin{align*}\partial_{i}(fg)=(\partial_{i}f)g+f(\partial_{i}g)\end{align*}
となり,これは$(\operatorname{grad}f)g+f(\operatorname{grad}g)$の第$i$成分に等しい($i=1,2,\dots,n$).
よって,$\operatorname{grad}(fg)=(\operatorname{grad}f)g+f(\operatorname{grad}g)$が成り立つ.
[$\operatorname{div}$について]
\begin{align*}
\operatorname{div}(f\m{v})
=&\sum_{i=1}^{n}\partial_i(fv_i)
\\=&\sum_{i=1}^{n}\{(\partial_{i}f)v_i+f(\partial_{i}v_i)\}
\\=&\sum_{i=1}^{n}(\partial_{i}f)v_i+f\sum_{i=1}^{n}\partial_{i}v_i
\\=&(\operatorname{div}f)\cdot\m{v}+f(\operatorname{div}\m{v})
\end{align*}
[$\operatorname{rot}$について]
\begin{align*}
\operatorname{rot}(f\m{v})
=&\bmat{\partial_y(fv_3)-\partial_z(fv_2)\\\partial_z(fv_1)-\partial_x(fv_3)\\\partial_x(fv_2)-\partial_y(fv_1)}
\\=&\bmat{\bra{(\partial_{y}f)v_3+f(\partial_{y}v_3)}-\bra{(\partial_{z}f)v_2+f(\partial_{z}v_2)}\\
\bra{(\partial_{z}f)v_1+f(\partial_{z}v_1)}-\bra{(\partial_{x}f)v_3+f(\partial_{x}v_3)}\\
\bra{(\partial_{x}f)v_2+f(\partial_{x}v_2)}-\bra{(\partial_{y}f)v_1+f(\partial_{y}v_1)}}
\\=&\bmat{(\partial_{y}f)v_3-(\partial_{z}f)v_2\\(\partial_{z}f)v_1-(\partial_{x}f)v_3\\(\partial_{x}f)v_2-(\partial_{y}f)v_1}
+\bmat{f(\partial_{y}v_3)-f(\partial_{z}v_2)\\f(\partial_{z}v_1)-f(\partial_{x}v_3)\\f(\partial_{x}v_2)-f(\partial_{y}v_1)}
\\=&(\operatorname{grad}f)\times\m{v}+f(\operatorname{rot}\m{v})
\end{align*}
いずれの場合も,高校数学以来親しんできた積の微分公式$(fg)’=f’g+fg’$と同様の形をしていますね.
内積・外積の微分公式
ベクトル値関数$\m{u},\m{v}:\R^3\to\R^3$に対して,
- 内積$\m{u}\cdot\m{v}:\R^n\to\R$は関数
- 外積$\m{u}\times\m{v}:\R^3\to\R^3$はベクトル値関数
となっていることに注意して下さい.これらについて,以下が成り立ちます.
ベクトル値関数$\m{u}=\bmat{u_1\\u_2\\u_3},\m{v}=\bmat{v_1\\v_2\\v_3}:\R^3\to\R^3$に対して,以下が成り立つ.
- $\operatorname{grad}(\m{u}\cdot\m{v})=\bmat{(\operatorname{grad}u_1)\cdot\m{v}\\(\operatorname{grad}u_2)\cdot\m{v}\\(\operatorname{grad}u_3)\cdot\m{v}}+\bmat{(\operatorname{grad}v_1)\cdot\m{u}\\(\operatorname{grad}v_2)\cdot\m{u}\\(\operatorname{grad}u_3)\cdot\m{u}}+\m{u}\times(\operatorname{rot}\m{v})+\m{v}\times(\operatorname{rot}\m{u})$
- $\operatorname{div}(\m{u}\times\m{v})=(\operatorname{rot}\m{u})\cdot\m{v}-\m{u}\cdot(\operatorname{rot}\m{v})$
- $\operatorname{rot}(\m{u}\times\m{v})=\bmat{(\operatorname{grad}u_1)\cdot\m{v}\\(\operatorname{grad}u_2)\cdot\m{v}\\(\operatorname{grad}u_3)\cdot\m{v}}-\bmat{(\operatorname{grad}v_1)\cdot\m{u}\\(\operatorname{grad}v_2)\cdot\m{u}\\(\operatorname{grad}u_3)\cdot\m{u}}+\m{u}(\operatorname{div}\m{v})-\m{v}(\operatorname{div}\m{u})$
[$\operatorname{grad}$について] $\operatorname{grad}(\m{u}\cdot\m{v})$の第1成分は
\begin{align*}
&\partial_{x}(\m{u}\cdot\m{v})
\\=&\partial_{x}(u_1v_1+u_2v_2+u_3v_3)
\\=&(\partial_{x}u_1)v_1+u_1(\partial_{x}v_1)+(\partial_{x}u_2)v_2+u_2(\partial_{x}v_2)+(\partial_{x}u_3)v_3+u_3(\partial_{x}v_3)
\\=&\{(\partial_{x}u_1)v_1+(\partial_{y}u_1)v_2+(\partial_{z}u_1)v_3\}
+\{(\partial_{x}v_1)u_1+(\partial_{y}v_1)u_2+(\partial_{z}v_1)u_3\}
\\&+\{u_2(\partial_{x}v_2-\partial_{y}v_1)-u_3(\partial_{z}v_1-\partial_{x}v_3)\}
+\{v_2(\partial_{x}u_2-\partial_{y}u_1)-v_3(\partial_{z}u_1-\partial_{x}u_3)\}
\\=&(\operatorname{grad}u_1)\cdot\m{v}+(\operatorname{grad}v_1)\cdot\m{u}
\\&+\bra{u_2\vmat{\partial_{x}&v_1\\\partial_{y}&v_2}-u_3\vmat{\partial_{z}&v_3\\\partial_{x}&v_1}}
+\bra{v_2\vmat{\partial_{x}&u_1\\\partial_{y}&u_2}-v_3\vmat{\partial_{z}&u_3\\\partial_{x}&u_1}}
\end{align*}
となり,これは$\bmat{(\operatorname{grad}u_1)\cdot\m{v}\\(\operatorname{grad}u_2)\cdot\m{v}\\(\operatorname{grad}u_3)\cdot\m{v}}+\bmat{(\operatorname{grad}v_1)\cdot\m{u}\\(\operatorname{grad}v_2)\cdot\m{u}\\(\operatorname{grad}u_3)\cdot\m{u}}+\m{u}\times(\operatorname{rot}\m{v})+\m{v}\times(\operatorname{rot}\m{u})$の第1成分に等しい.
各成分の対称性から第2成分,第3成分でも両辺が等しいことが分かる.
[$\operatorname{div}$について]
\begin{align*}
&\operatorname{div}(\m{u}\times\m{v})
\\=&\partial_{x}\vmat{u_2&v_2\\u_3&v_3}+\partial_{y}\vmat{u_3&v_3\\u_1&v_1}+\partial_{z}\vmat{u_1&v_1\\u_2&v_2}
\\=&\partial_{x}(u_2v_3-u_3v_2)+\partial_{y}(u_3v_1-u_1v_3)+\partial_{z}(u_1v_2-u_2v_1)
\\=&[\{(\partial_{x}u_2)v_3+u_2(\partial_{x}v_3)\}-\{(\partial_{x}u_3)v_2+u_3(\partial_{x}v_2)\}]
\\&+[\{(\partial_{y}u_3)v_1+u_3(\partial_{y}v_1)\}-\{(\partial_{y}u_1)v_3+u_1(\partial_{y}v_3)\}]
\\&+[\{(\partial_{z}u_1)v_2+u_1(\partial_{z}v_2)\}-\{(\partial_{z}u_2)v_1+u_2(\partial_{z}v_1)\}]
\\=&\{(\partial_{y}u_3-\partial_{z}u_2)v_1+(\partial_{z}u_1-\partial_{x}u_3)v_2+(\partial_{x}u_2-\partial_{y}u_1)v_3\}
\\&-\{(\partial_{y}v_3-\partial_{z}v_2)u_1+(\partial_{z}v_1-\partial_{x}v_3)u_2+(\partial_{x}v_2-\partial_{y}v_1)u_3\}
\\=&\bra{\vmat{\partial_{y}&u_2\\\partial_{z}&u_3}v_1+\vmat{\partial_{z}&u_3\\\partial_{x}&u_1}v_2+\vmat{\partial_{x}&u_1\\\partial_{y}&u_2}v_3}
\\&-\bra{u_1\vmat{\partial_{y}&v_2\\\partial_{z}&v_3}+u_2\vmat{\partial_{z}&v_3\\\partial_{x}&v_1}+u_3\vmat{\partial_{x}&v_1\\\partial_{y}&v_2}}
\\=&(\operatorname{rot}\m{u})\cdot\m{v}-\m{u}\cdot(\operatorname{rot}\m{v})
\end{align*}
[$\operatorname{rot}$について] $\operatorname{rot}(\m{u}\times\m{v})$の第1成分は
\begin{align*}
&\vmat{\partial_{y}&u_3v_1-u_1v_3\\\partial_{z}&u_1v_2-u_2v_1}
\\=&\partial_{y}(u_1v_2-u_2v_1)-\partial_{z}(u_3v_1-u_1v_3)
\\=&[\{(\partial_{y}u_1)v_2+u_1(\partial_{y}v_2)\}-\{(\partial_{y}u_2)v_1+u_2(\partial_{y}v_1)\}]
\\&-[\{(\partial_{z}u_3)v_1+u_3(\partial_{z}v_1)\}-\{(\partial_{z}u_1)v_3+u_1(\partial_{z}v_3)\}]
\\=&\{(\partial_{x}u_1)v_1+(\partial_{y}u_1)v_2+(\partial_{z}u_1)v_3\}-\{(\partial_{x}v_1)u_1+(\partial_{y}v_1)u_2+(\partial_{z}v_1)u_3\}
\\&+u_1(\partial_{x}v_1+\partial_{y}v_2+\partial_{z}v_3)-v_1(\partial_{x}u_1+\partial_{y}u_2+\partial_{z}u_3)
\\=&(\operatorname{grad}u_1)\cdot\m{v}-(\operatorname{grad}v_1)\cdot\m{u}+u_1(\operatorname{div}\m{v})-v_1(\operatorname{div}\m{u})
\end{align*}
となり,これは$\bmat{(\operatorname{grad}u_1)\cdot\m{v}\\(\operatorname{grad}u_2)\cdot\m{v}\\(\operatorname{grad}u_3)\cdot\m{v}}-\bmat{(\operatorname{grad}v_1)\cdot\m{u}\\(\operatorname{grad}v_2)\cdot\m{u}\\(\operatorname{grad}u_3)\cdot\m{u}}+\m{u}(\operatorname{div}\m{v})-\m{v}(\operatorname{div}\m{u})$の第1成分に等しい.
各成分の対称性から第2成分,第3成分でも両辺が等しいことが分かる.
先ほどの公式よりも少し複雑ですが,やはりいずれの場合も単純な計算で導けますね.
ナブラ$\nabla$を用いた形
ナブラ$\nabla:=\bmat{\partial_1\\\vdots\\\partial_n}$を用いると,以上の公式は次のようになります.
定数$\alpha,\beta\in\R$に対して,次が成り立つ.
- $\nabla(\alpha f+\beta g)=\alpha\nabla f+\beta\nabla g$
- $\nabla\cdot(\alpha \m{u}+\beta\m{v})=\alpha\nabla\cdot\m{u}+\beta\nabla\cdot\m{v}$
- $\nabla\times(\alpha \m{u}+\beta\m{v})=\alpha\nabla\times\m{u}+\beta\nabla\times\m{v}$
関数$f,g:\R^n\to\R$とベクトル値関数$\m{v}:\R^n\to\R^n$に対して,以下が成り立つ.
- $\nabla(fg)=(\nabla f)g+f(\nabla g)$
- $\nabla\cdot(f\m{v})=(\nabla f)\cdot\m{v}+f(\nabla\cdot\m{v})$
- $\nabla\times(f\m{v})=(\nabla f)\times\m{v}+f(\nabla\times\m{v})$
ベクトル値関数$\m{u},\m{v}:\R^3\to\R^3$に対して,以下が成り立つ.
- $\nabla(\m{u}\cdot\m{v})=(\nabla\otimes\m{u})^T\m{v}+(\nabla\otimes\m{v})^T\m{u}+\m{u}\times(\nabla\times\m{v})+\m{v}\times(\nabla\times\m{u})$
- $\nabla\cdot(\m{u}\times\m{v})=(\nabla\times\m{u})\cdot\m{v}-\m{u}\cdot(\nabla\times\m{v})$
- $\nabla\times(\m{u}\times\m{v})=(\nabla\otimes\m{u})^T\m{v}-(\nabla\otimes\m{v})^T\m{u}+\m{u}(\nabla\cdot\m{v})-\m{v}(\nabla\cdot\m{u})$
ただし,最後の内積・外積に関する微分公式について,$\nabla\otimes\m{v}$は
\begin{align*}
(\nabla\otimes\m{v})^T
=&\bmat{\partial_{x}v_1&\partial_{y}v_1&\partial_{z}v_1\\\partial_{x}v_2&\partial_{y}v_2&\partial_{z}v_2\\\partial_{x}v_3&\partial_{y}v_3&\partial_{z}v_3}
\\=&\bmat{(\operatorname{grad}v_1)^T\\(\operatorname{grad}v_2)^T\\(\operatorname{grad}u_3)^T}
=\bmat{(\nabla v_1)^T\\(\nabla v_2)^T\\(\nabla u_3)^T}
\end{align*}
で定まるベクトルです.

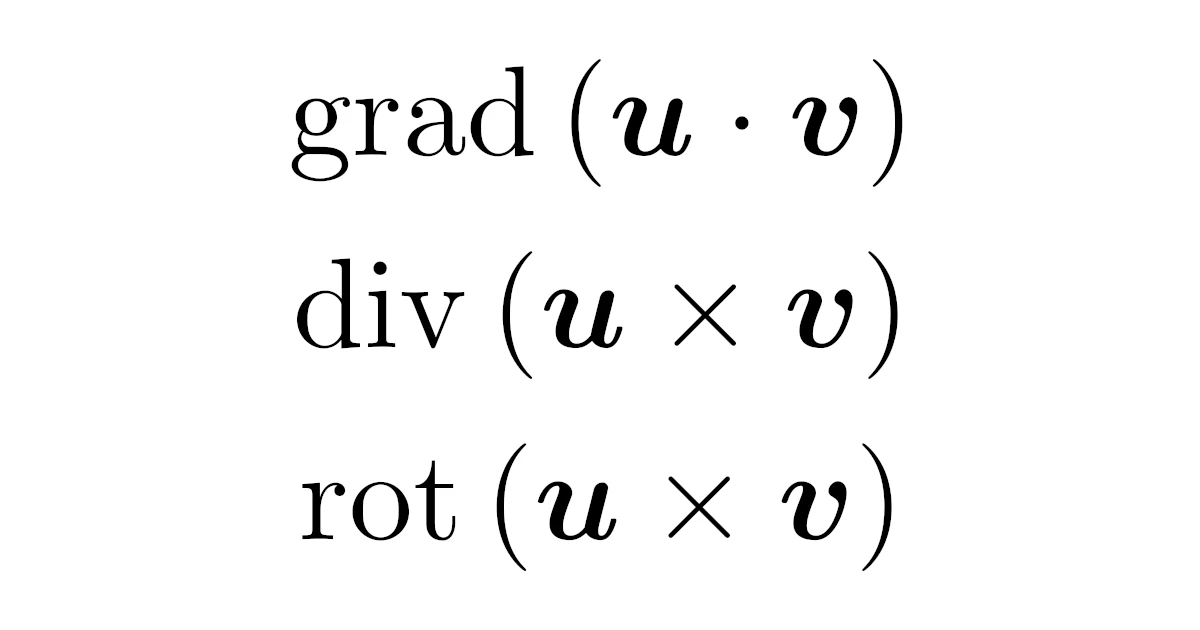
コメント