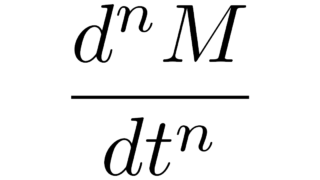 確率論
確率論 積率母関数の微分可能性|$n$次モーメントが得られることの証明
実数値確率変数Xに対して,Xの積率母関数E[exp(tX)]のn階導関数に0を代入すると,Xのn次モーメントE[Xⁿ]が得られます.この記事では,この積率母関数とモーメントの関係をルベーグの収束定理を用いて証明します.
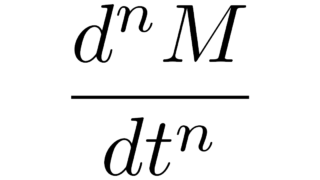 確率論
確率論  確率論
確率論  確率論
確率論 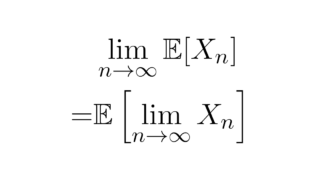 確率論
確率論  確率論
確率論