確率論の重要な定理に中心極限定理があります.
大雑把に言えば,中心極限定理とは「同じ分布に従う独立試行を何度も繰り返すと,トータルで見れば正規分布っぽくなる」という定理です.
本記事は「二項分布のシミュレートを用いて,中心極限定理がどういうものか実感しよう」というものです.
本記事ではJuliaというプログラミング言語を扱っていますが,本記事の主題は中心極限定理のイメージを理解することなので,Juliaのコードが分からなくても問題ないように話を進めます.
二項分布$\mrm{Bin}(n,p)$を$n$を変えてシミュレートする
中心極限定理の説明のために,先に「表が確率$p$で出るいびつなコインを投げて何回表が出るか?」という二項分布のシミュレートをしてみましょう.
ここでは,試行回数$n$回,表が出る確率$p=0.3$の二項分布$\mrm{Bin}(n,0.3)$を考えます.
つまり,「表が30%の確率で出る歪んだコインを$n$回投げたときに,合計で何回表が出るか」を考えます.
$\mrm{Bin}(10,0.3)$のシミュレート
$n=10$の二項分布$\mrm{Bin}(10,0.3)$をシミュレートしましょう.
つまり,「表が30%の確率で出る歪んだコインを10回投げたときに,合計で何回表が出るか」をシミュレートします.
直観的には,10回中に表が出る回数は$10\times0.3=3$より3回が多そうです.実際に「表が30\%の確率で出る歪んだコインを10回投げて,表が出る回数を記録する」という試行を100回シミュレートしてみましょう.
1回の試行が「コインを10回投げる」なので,全部で10×100=1000回コインを投げることになります.
各回ごとの表が出た回数
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
using Plots;gr() p = 0.3 #コイン投げの表の確率 n = 10 #コイン投げをする回数 N = 100 #試行回数 face = zeros(N) #N回それぞれの試行での表の回数を全て0にセットする for I = 1:N #N回中I回目を考える coin = rand(n) #n個の乱数(0〜1)を生成する(n個のサイコロをふる) for i = 1:n if coin[i] < p face[I] += 1 #i個目の乱数が0.3未満なら表とみなして,I回目の表の表の回数に+1 end end end plot(face, label = "", color = :red, marker = :auto) #各試行での表の回数 |
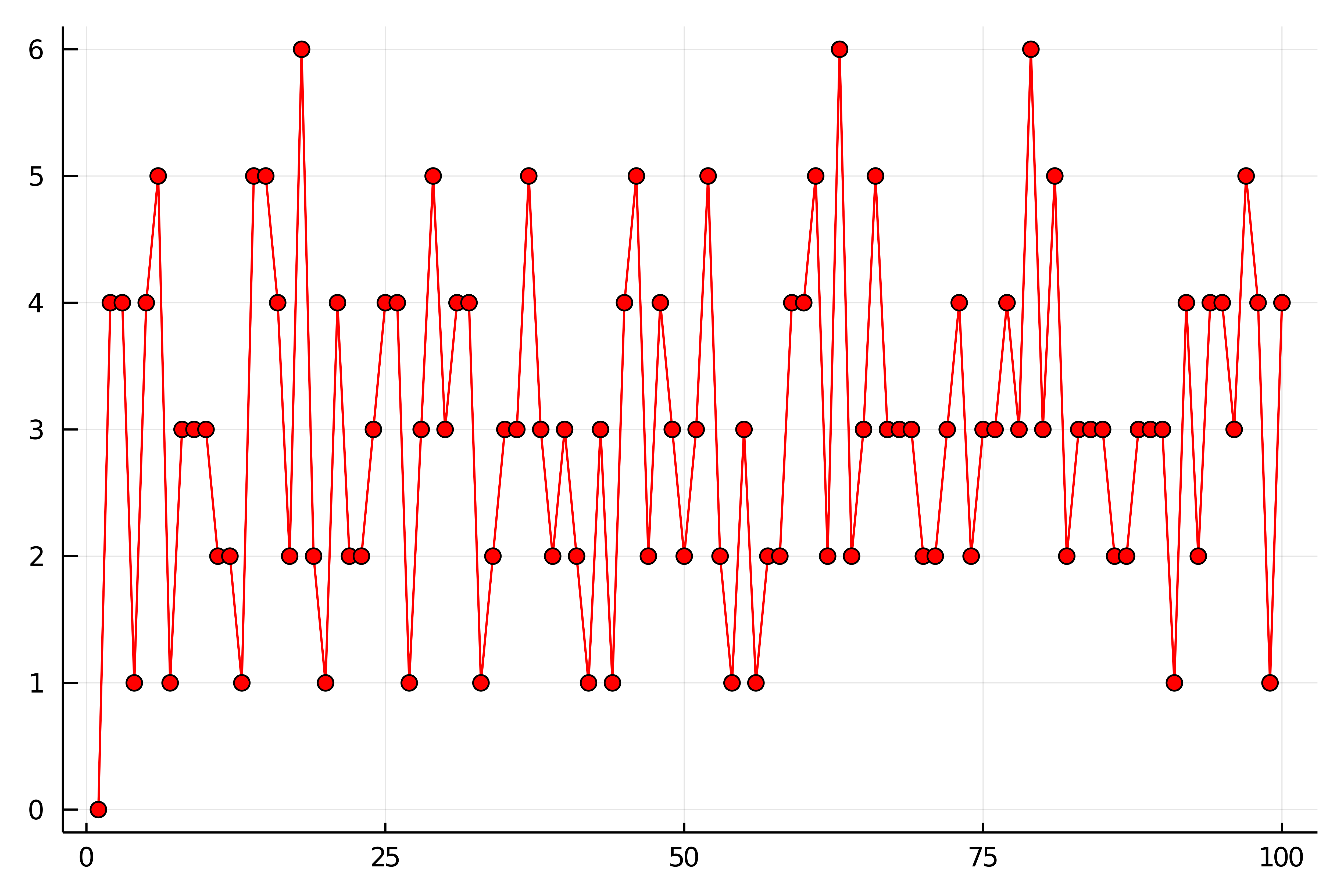
1回目は表が1回も出なかったようで,17回目と63回目と79回目に表が6回出ていてこれが最高の回数ですね.
この図を見ると,3回表が出ている試行が最も多いように見えますね.
表が出た回数のヒストグラム
表が出た回数をヒストグラムに直してみましょう.
|
1 |
plot(face, label = "", color = :red, st = :histogram) #ヒストグラム |
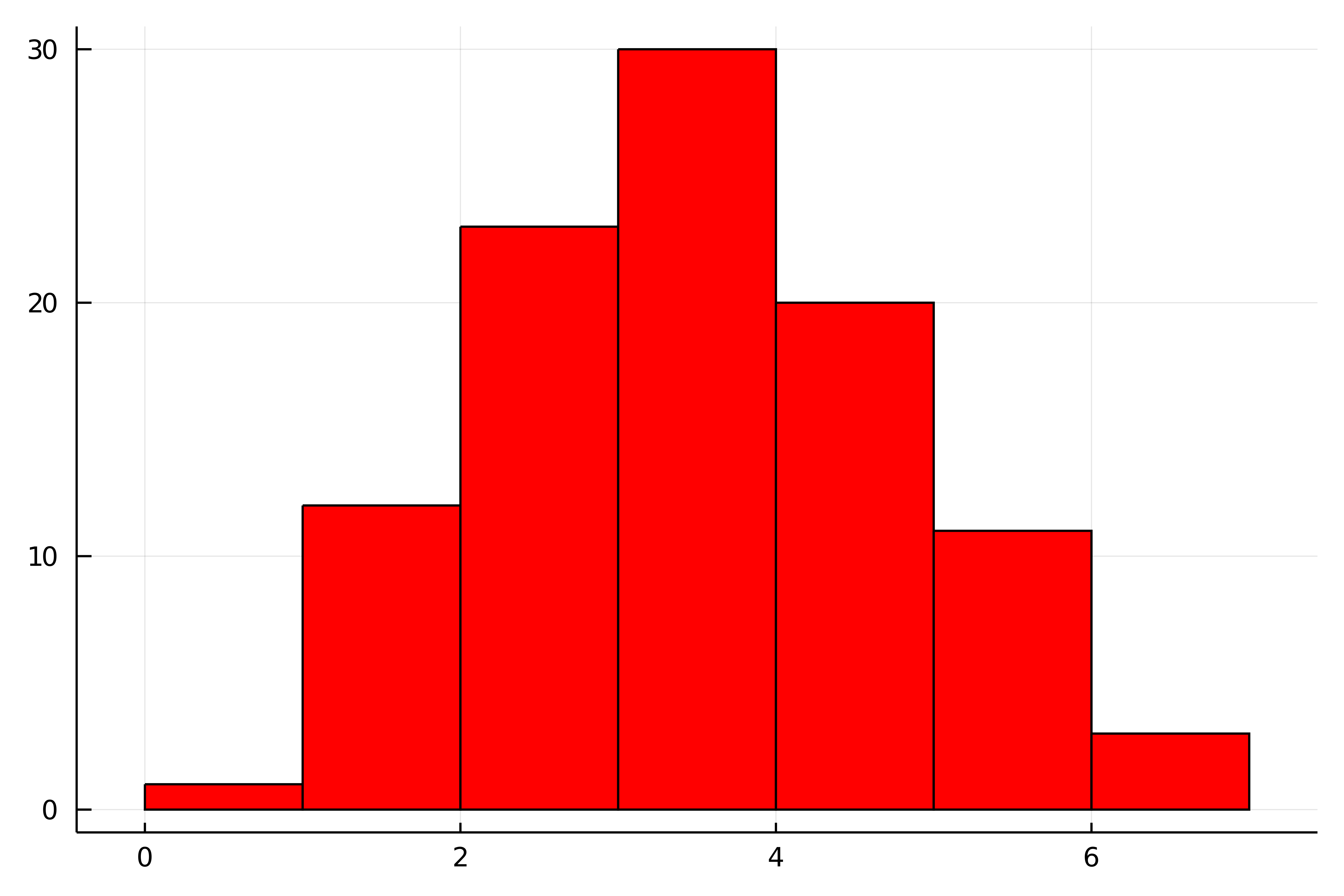
確かに,3回表が出た試行が最も多く30回となっていますね.
$\mrm{Bin}(30,0.3)$のシミュレート
$n=30$の二項分布$\mrm{Bin}(30,0.3)$をシミュレートしましょう.
つまり,「表が30%の確率で出る歪んだコインを30回投げたときに,合計で何回表が出るか」をシミュレートします.
今回は「30回コインを投げて表の回数を記録する」という1回の試行を10000回シミュレートしてみます.表が出た回数をヒストグラムは次のようになりました.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
using Plots;gr() p = 0.3 #コイン投げの表の確率 n = 30 #コイン投げをする回数 N = 10000 #試行回数 face = zeros(N) #N回それぞれの試行での表の回数を全て0にセットする for I = 1:N #N回中I回目を考える coin = rand(n) #n個の乱数(0〜1)を生成する(n個のサイコロをふる) for i = 1:n if coin[i] < p face[I] += 1 #i個目の乱数が0.3未満なら表とみなして,I回目の表の表の回数に+1 end end end plot(face, label = "", color = :red, st = histogram) #各試行での表の回数 |
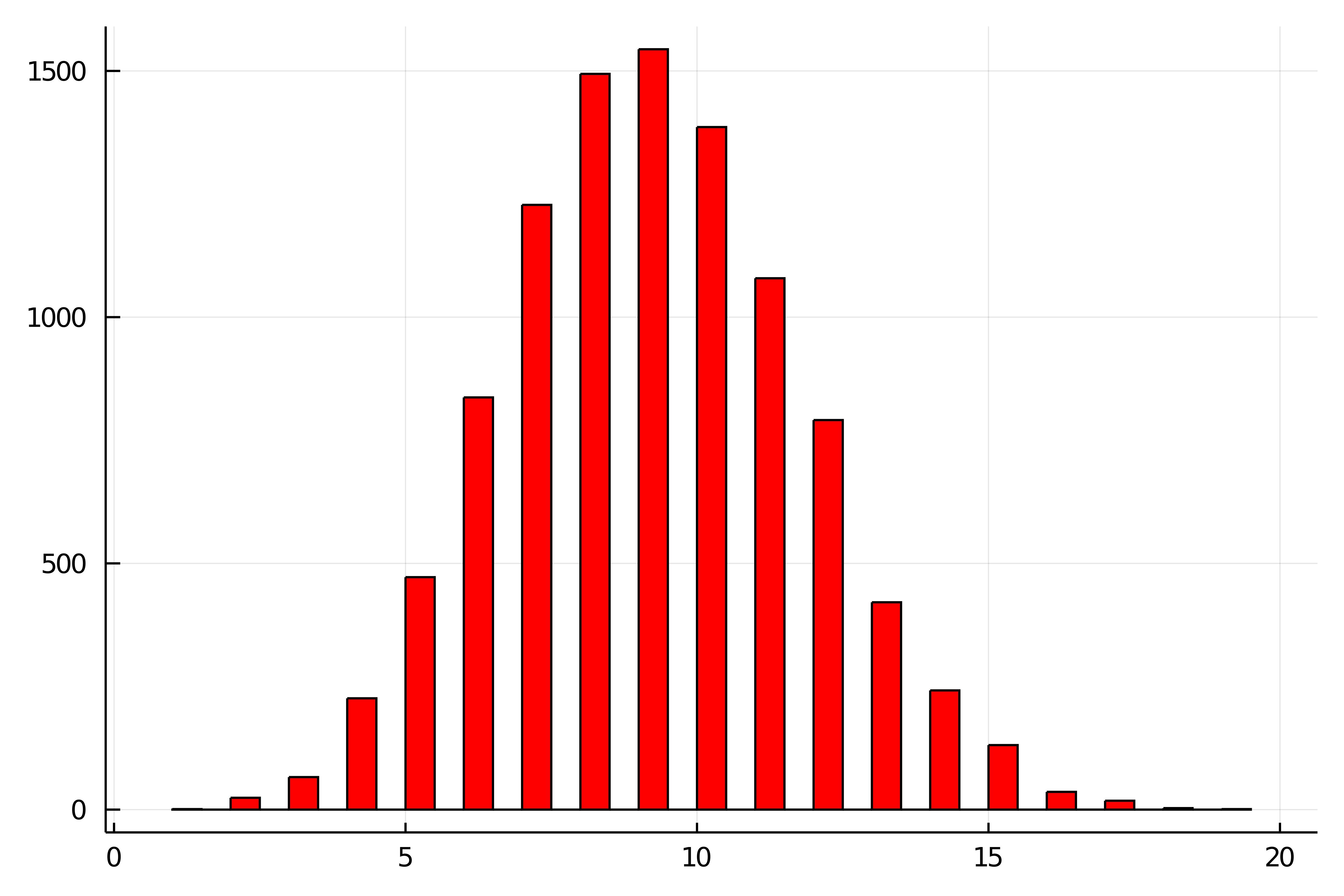
1回の試行でコインを10回投げる二項分布$\mrm{Bin}(10,0.3)$よりも,ヒストグラムはガタガタではなくなってきたように見えます.
$\mrm{Bin}(100,0.3)$のシミュレート
$n=100$の二項分布$\mrm{Bin}(100,0.3)$をシミュレートしましょう.
つまり,「表が30%の確率で出る歪んだコインを100回投げたときに,合計で何回表が出るか」をシミュレートします.
今回は「100回コインを投げて表の回数を記録する」という1回の試行を1000000回(百万回)シミュレートしてみます.表が出た回数をヒストグラムは次のようになりました(コードは省略).
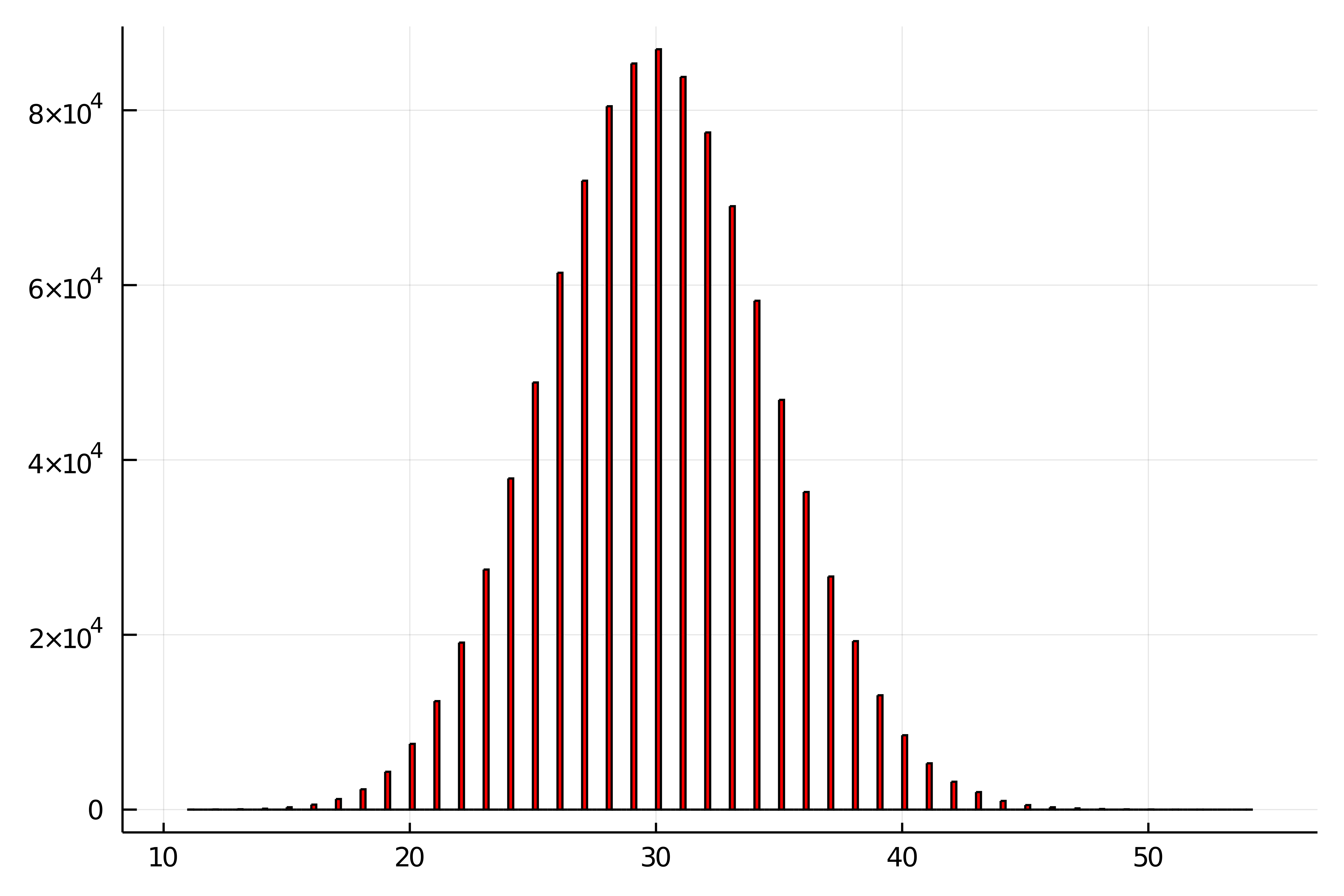
とても綺麗な釣鐘型になっていて,正規分布の確率密度関数に近いように見えますね!
このように,二項分布$\mrm{Bin}(n,p)$は$n$を大きくしていくと,正規分布のようになりそうなことが分かりました.
ベルヌーイ分布と二項分布の準備
ここで,準備としてベルヌーイ分布,二項分布を確認しておきましょう.
ベルヌーイ分布$\mrm{Ber}(p)$の定義
表が出る確率が$p$のいびつなコインを投げて
- 表が出れば1点
- 裏が出れば2点
という「ゲーム$X$」を考えます.
このゲーム$X$のように確率的に事象が変化する事柄の結果(事象)に応じて,値を返す関数を確率変数といいます.
実数$p$は$0<p<1$を満たすとする.離散型確率変数$X$がパラメータ$p$のベルヌーイ分布(Bernoulli distribution)に従うとは,$X$の確率関数$p_X$が
\begin{align*}p_X(1)=p,\quad p_X(0)=1-p\end{align*}
を満たすことをいう.また,このとき$X\sim\mrm{Ber}(p)$などと表す.
二項分布$\mrm{Bin}(n,p)$の定義
ベルヌーイ分布でも考えた表が出る確率が$p$のいびつなコインを$n$回投げて,表が出た回数を得点とする「ゲーム$Y$」を考えます.
このゲーム$Y$はゲーム$X$を繰り返し行って点数を加算していくゲームと言えるので,ゲーム$Y$の$k$回目のコイン投げをゲーム$X_k$と呼ぶことにすれば
\begin{align*}Y=X_1+X_2+\dots+X_n\end{align*}
と表すことができますね.

$p$を$0<p<1$を満たす実数とし,$n$を正の整数とする.離散型確率変数$Y$がパラメータ$n$, $p$の二項分布(binomial distribution)に従うとは,$Y$の確率関数$p_Y$が
\begin{align*}p_Y(k)=\binom{n}{k}p^{k}(1-p)^{n-k}\end{align*}
を満たすことをいう.また,このとき$X\sim\mrm{Bin}(n,p)$などと表す.
$\binom{n}{m}$は二項係数で,高校数学で学ぶ組み合わせの場合の数${}_{n}\!\operatorname{C}_{m}$と同じです:$\binom{n}{m}=\frac{n!}{m!(n-m)!}$.
中心極限定理をシミュレーションから理解する
次に,中心極限定理の主張を確認して,シミュレーションが中心極限定理に沿っていることを確認しましょう.
中心極限定理(CLT)の主張
二項分布$\mrm{Bin}(n,p)$に従う確率変数$Y$は,ベルヌーイ分布$\mrm{Ber}(p)$に従う独立な確率変数$X_1,\dots,X_n$の和として表せるのでした:$Y=X_1+\dots+X_n$.

この和$Y$が$n$を大きくすると正規分布の確率密度関数のような形状に近付くことは上でシミュレートした通りですが,実は$X_1,\dots,X_n$がベルヌーイ分布でなくても,同一の確率分布に独立に従う確率変数$X_1,\dots,X_n$の和でも同じことが起こります.
この定理を中心極限定理(central limit theorem,CLT)といいます.
厳密に述べると次のようになりますが,よく分からない方は飛ばしても構いません.
[中心極限定理]平均$\mu\in\R$,分散$\sigma^2\in(0,\infty)$の同一の確率分布に従う独立な確率変数列$X_1,X_2,\dots$に対して
\begin{align*}Z_n:=\frac{1}{\sqrt{n\sigma^2}}\sum_{k=1}^{n}(X_k-\mu)\end{align*}
で定まる確率変数列$Z_1,Z_2,\dots$は,標準正規分布$\mrm{N}(0,1)$に従う確率変数$Z$に法則収束する:
\begin{align*}Z_n\xrightarrow[]{\mathcal{L}}Z\sim\mathcal{N}(0,1).\end{align*}
ここでは「$n$が十分大きければ確率変数
\begin{align*}Z_n=\frac{1}{\sqrt{n\sigma^2}}\sum_{k=1}^{n}(X_k-\mu)\quad\dots(*)\end{align*}
は$n$が大きいとき,だいたい標準正規分布$\mrm{N}(0,1)$に従う」という程度の理解で問題ありません.
さて,式$(*)$を変形すると
\begin{align*}X_1+\dots+X_n=\sqrt{n\sigma^2}Z_n+n\mu\end{align*}
となりますから,確率変数$X_1+\dots+X_n$は確率変数$\sqrt{n\sigma^2}Z+n\mu$に近いと言えますね.
確率変数に数をかけても縮尺が変わるだけですし,数を足しても平行移動するだけなので,結果として$X_1+\dots+X_n$のシミュレーションのヒストグラムは正規分布と同じく釣鐘型に近くなるわけですね.
シミュレートと正規分布を比較する
先ほどシミュレートした$n=100$の場合のヒストグラムは1000000回のシミュレートなので,ヒストグラムの度数を1000000で割ると二項分布$\mrm{Bin}(100,0.3)$の確率関数がシミュレートされますね.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
using Plots;gr() using LaTeXStrings p = 0.3 #コイン投げの表の確率 n = 100 #コイン投げをする回数 N = 1000000 #試行回数 face = zeros(N) #N回それぞれの試行での表の回数を全て0にセットする for I = 1:N #N回中I回目を考える coin = rand(n) #n個の乱数(0〜1)を生成する(n個のサイコロをふる) for i = 1:n if coin[i] < p face[I] += 1 #i個目の乱数が0.3未満なら表とみなして,I回目の表の回数に+1 end end end distribution = zeros(n) #n回表が出る確率を全て0にセットする for i = 1:n #i回表が出る場合を考える for I = 1:N if face[I] == i distribution[i] += 1/N #I回目の試行で表がi回出ていれば,i回の表が出る確率に+1/N end end end plot(distribution, label = "", color = :red, linewidth=2) #Bin(100,0.3)の分布関数 |
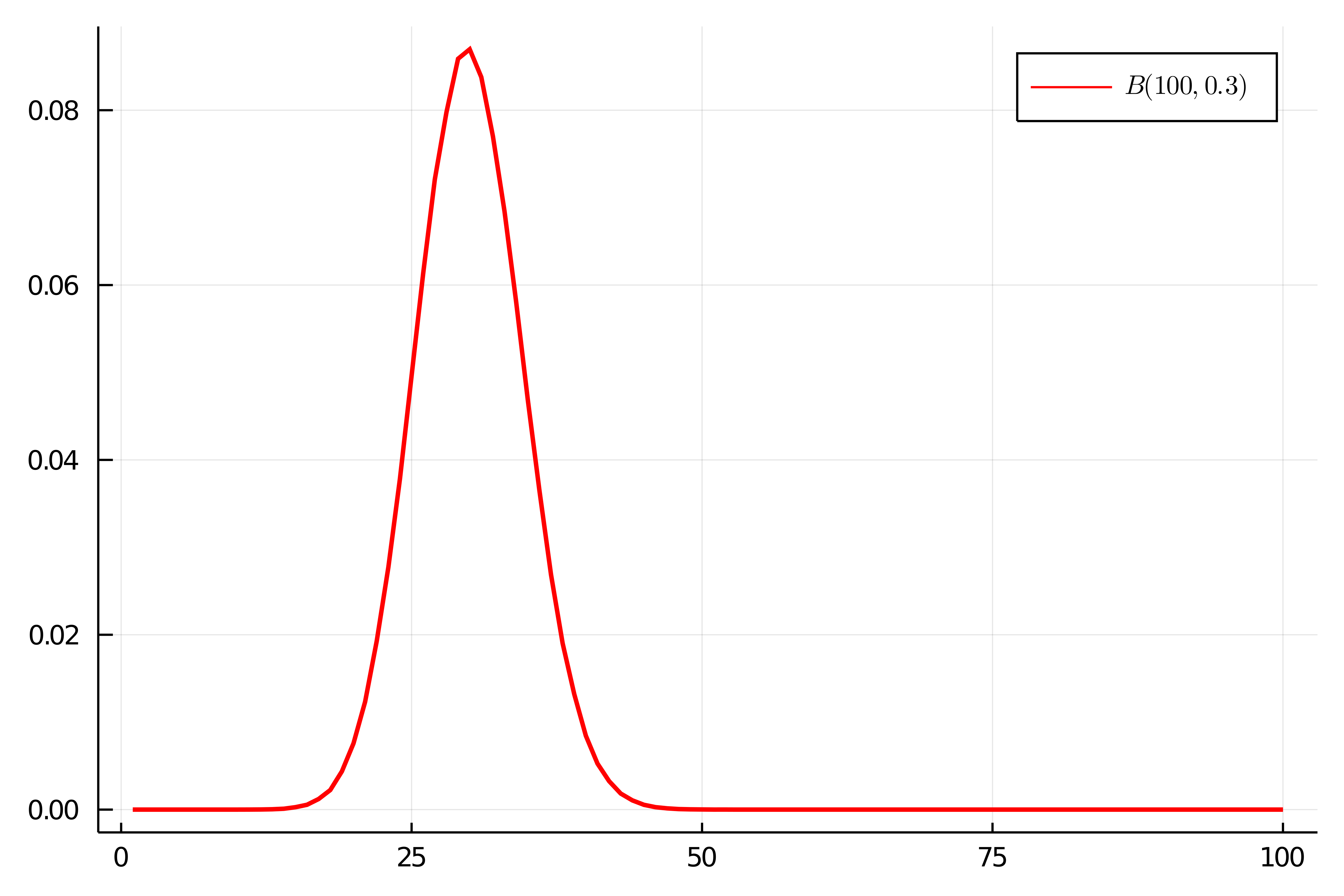
一般に,ベルヌーイ分布$\mrm{Ber}(p)$に従う確率変数$X$については
- 平均は$E[X]=p$
- 分散は$V[X]=p(1-p)$
なので,中心極限定理より二項分布$\mrm{Bin}(100,0.3)$に従う確率変数$X_1+\dots+X_{100}$($X_1,\dots,X_{100}\sim\mrm{Ber}(0.3)$)は,確率変数
\begin{align*}\sqrt{100\times0.3\cdot(1-0.3)}Z+100\cdot0.3\cdot(1-0.3)=\sqrt{21}Z+30\end{align*}
に十分近いはずです.この確率変数は
- 平均は$30$
- 分散は$21$
の正規分布に従うので,この確率密度関数を上でシミュレートした$\mrm{Bin}(100,0.3)$の確率関数と重ねて表示させると次のようになります.
|
1 2 3 4 5 6 |
mu = n*p Sigma = n*p*(1-p) f(x) = exp(-(x-mu)^2/(2*Sigma))/sqrt(2*pi*Sigma) #平均30,分散21の正規分布の確率密度関数 x = range(0,100; length = 2001) plot!(x,f.(x); label = L"\mathcal{N}(30,21)", color = :blue, linewidth=1, style = :dash) #中心極限定理 |
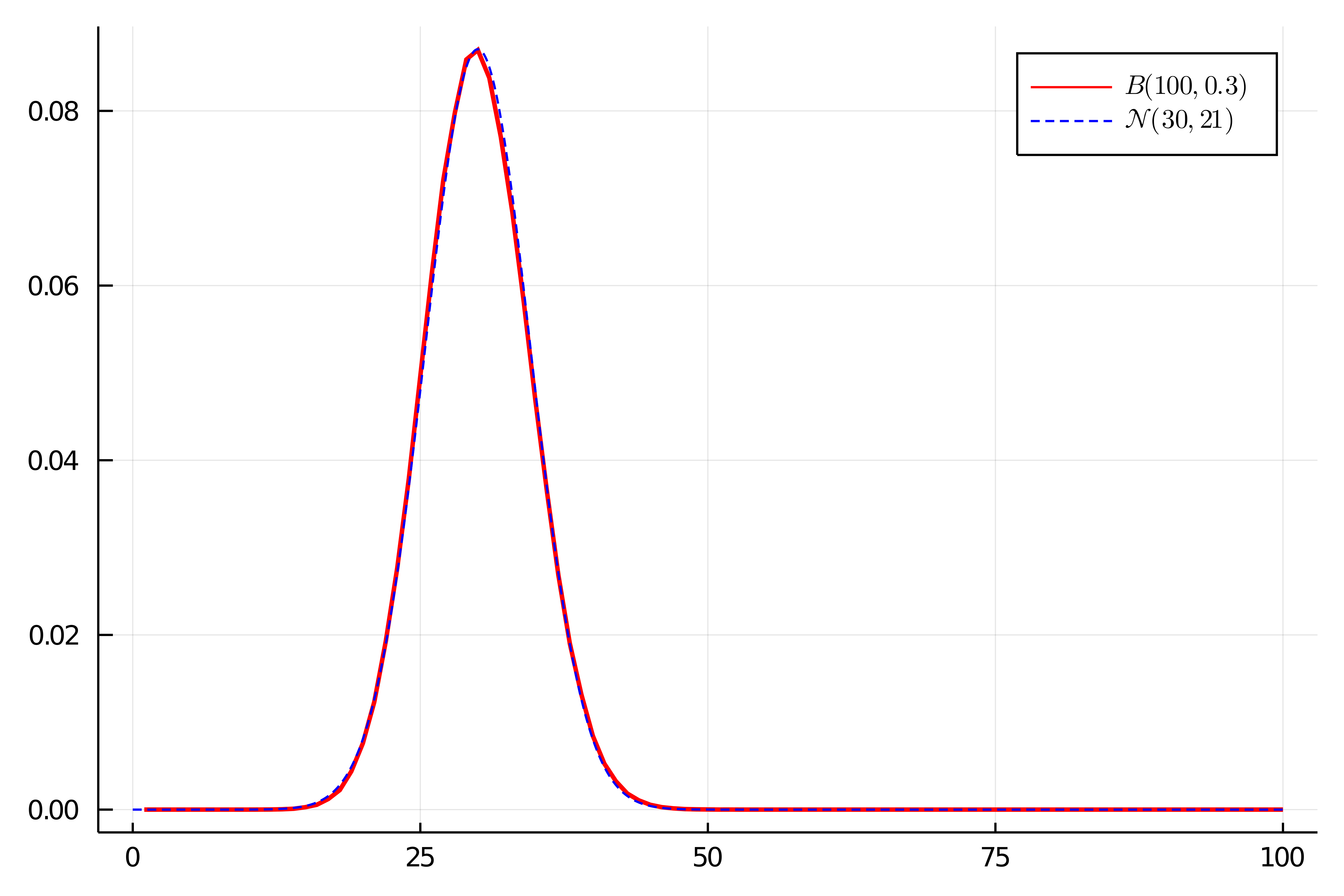
確かに両者が近いことが見てとれますね!
よって,確かにシミュレーションから中心極限定理が成り立っていそうなことが分かりました.

コメント